初中数学毕业生学业考试试卷
数 学
考生须知：
1．全卷满分为150分，考试时间120分钟．试卷共4页，有三大题，24小题．
2．本卷答案必须做在答题卷Ⅰ、Ⅱ的相应位置上，做在试卷上无效．答卷Ⅰ共1页、答卷Ⅱ共4页．
3．请用钢笔或圆珠笔将姓名、准考证号分别填写在答题卷Ⅰ、Ⅱ的相应位置上．
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！
参考公式：二次函数y=ax2+bx+c的顶点坐标是
．
试 卷 Ⅰ
请用铅笔将答卷Ⅰ上的准考证号和学科名称所对应的括号或方框内涂黑，然后开始答题．
一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
1. 计算
的结果是（ ）
A、
B、
C、
D、3
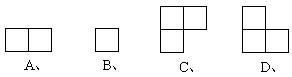
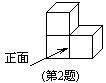2. 如右图，由三个小立方体搭成的几何体的俯视图是（ ）
3. 二次函数y=x2的图象向上平移2个单位，得到新的图象的二次函数表达式是（ ）
A、
B、
C、
D、
4. 在
中，
，AB=15，sinA=
，则BC等于（ ）
A、45 B、5 C、
D、
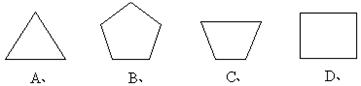5. 下列图形中，既是轴对称图形，又是中心对称图形的是 ( )
6. 某住宅小区六月份中1日至6日每天用水量变化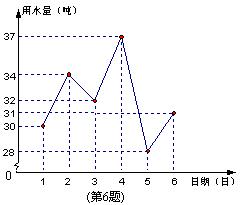
情况如图所示，那么这6天的平均用水量是（ ）
A、30吨 B、31吨
C、32吨 Ｄ、33吨
7. 一个扇形的圆心角是120°，它的面积为3πcm2，那么这个扇形的半径是（ ）
A、
cm Ｂ、3cm Ｃ、6cm Ｄ、9cm
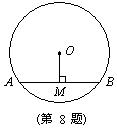
8. 如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长
是（ ）
A、4 B、6
C、7 D、8
9. 根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是（ ）
A、3＜x＜3.23 B、3.23＜x＜3.24
C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
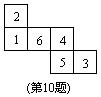10. 一个均匀的立方体六个面上分别标有数1，2，3，4，5，6．右图是这个立方体表面的展开图．抛掷这个立方体，则朝上一面上的数恰好等于朝下一面上的数的
的概率是（ ）
A、
B、 C、 D、
试 卷 Ⅱ
请将本卷的答案或解答过程用钢笔或圆珠笔写在答卷Ⅱ上．
二、填空题（本题有6小题，每小题5分，共30分）
11. 点P(1，2)关于y轴对称的点的坐标是 ．
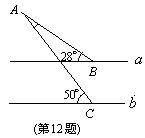
12. 如图所示，直线a∥b，则∠A= 度．
13. 已知⊙O的半径为8, 圆心O到直线l的距离是6, 则直线l与⊙O的位置关系是 ．
14. 如果直角三角形的斜边与一条直角边的长分别是13cm和5cm，那么这个直角三角形的面积是 cm2．
15. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式
，因式分解的结果是
，若取x=9，y=9时，则各个因式的值是：(x－y)=0，(x+y)=18，(x2+y2)=162，于是就可以把“018162”作为一个六位数的密码．对于多项式
，取x=10，y=10时，用上述方法产生的密码是： (写出一个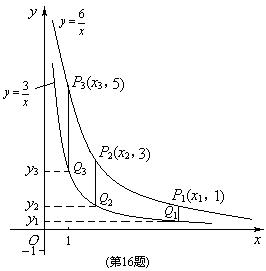
即可)．
16. 两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2 005，纵坐标分别是1，3，5，…，共2 005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17. (1) 计算：
-
； (2) 解方程：
．
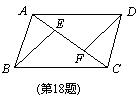
18. 如图，在□ABCD中，E，F是对角线AC上的两点，且AE=CF．
求证：BE=DF．
19. 我国政府在农村扶贫工作中取得了显著成效．据国家统计局公布的数据表明，2004年末我国农村绝对贫困人口为2 610万人(比上年末减少290万人)，其中东部地区为374万人，中部地区为931万人，西部地区为1 305万人．请用扇形统计图表示出2004年末这三个地区农村绝对贫困人口分布的比例(要在图中注明各部分所占的比例)．
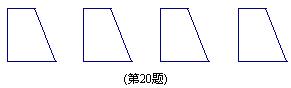20. 请将四个全等直角梯形(如图)，拼成一个平行四边形，并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法)．
21. 一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2．求x的取值范围．
22. 某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．
(1) 写出所有选购方案(利用树状图或列表方法表示）；
(2) 如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．
23. 据了解，火车票价按“
”的方法来确定．已知A站至H站总里程数为1 500千米，全程参考价为180元．下表是沿途各站至H站的里程数：
| 车站名 | A | B | C | D | E | F | G | H |
| 各站至H站的里程数（单位：千米） | 1500 | 1130 | 910 | 622 | 402 | 219 | 72 | 0 |
例如，要确定从B站至E站火车票价，其票价为
(元)．
(1) 求A站至F站的火车票价(结果精确到1元)；
(2) 旅客王大妈乘火车去女儿家，上车过两站后拿着火车票问乘务员：我快到站了吗？乘务员看到王大妈手中票价是66元，马上说下一站就到了．请问王大妈是在哪一站下车的？（要求写出解答过程）．
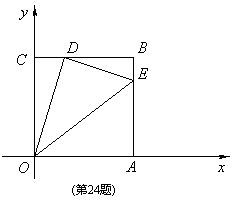24. 如图，边长为1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动(不与B，C重合)，连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．记CD的长为t．
(1) 当t＝时，求直线DE的函数表达式；
(2) 如果记梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由；
(3) 当OD2＋DE 2的算术平方根取最小值时，
求点E的坐标．
参考答案：
1． A 2． A 3． C 4． B 5． D 6． C 7． B 8． D 9． C 10． A 11． (－1，2) 12． 22º 13． 相交 14． 30 15． 101030等 16． 
17．（1）
（2） x＝－4 18． 略 19．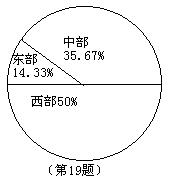
20． 略 21． 
22． （1）树状图：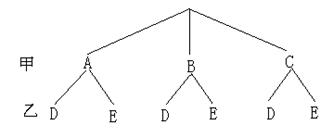
或列表法：
| 乙 甲 | D | E |
| A | （A，D） | （A，E） |
| B | （B，D） | （B，E） |
| C | （C，D） | （C，E） |
（2）A型号电脑被选中的概率是
（3）购买的A型号电脑有7台.
23．（1）154元 （2）G站下车 24． （1）
（2）存在最大值，当
时，S最大值为
（3）E（1，
）