初中数学练习(一)

初中数学练习 (一)

本试卷共4页，全卷三大题25小题，满分150分，考试时间120分钟。

注意事项：

1． 答卷前，考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、

座位号，再用2B铅笔把对应这两个号码的标号涂黑。

2．　　　 选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净

后，再选涂其他答案；不能答在试卷上。

3．　　　 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；

如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域；不准使用铅笔、圆珠笔和涂改液。涉及作图的题目，用2B铅笔画图。不按以上要求作答的答案无效。

4．　　　 考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。

一、选择题 (本题共10小题，每小题3分，满分30分)

1.　　　 的相反数为 （ * ）

　(A) -3　　　 　　　(B) 3　　　　 　　 (C)　　　　　　　　(D)　

2.　　　 设,是一元二次方程的两个根，则的值为（ * ）

（A）　　　　  （B）　　　　　 （C）　　　　  （D）0

3.　　　 下列运算正确的是（ * ）

（A）　　　　　　　 （B）

（C）　　　　　　　　（D）

　

4.　　　 我国的国土面积为平方千米，把这个数字保留三个有效数字，并用科学记数法表示为（ * ）

（A）平方千米　　　　　  　（B）平方千米　　　　

（C）平方千米　　　　　　　 （D）平方千米

5.　　　 下列交通标志图中，属于轴对称图形的是（ * ）

　

（A）　　　　　　 （B）　　　　　　  （C）　　　　　  （D）

6.　　　 在△ABC中，∠C=90°，AC=5，AB=13，则cosB的值为（ * ）

 (A) 　　　　　 (B) 　　　　　 (C) 　　　　　　　 (D)

7.　　　 某校学生参加环保知识竞赛，将参赛学生的成绩(得分取整数)进行整理后分成五组,绘成频率分布直方图如图，图中从左起第一、二、三、四、五个小长方形的高的比是1：3：6：4：2，第五组的频数为6，则成绩在60分以上(含60分)的同学的人数为

（A）43　　　（B）44　　　（C）45　　　 （D）48

 

8.　　　 如果正六边形的外接圆半径为R，那么这个正六边形的边长为（ *  ）

（A）R　　　　 （B）R　　　　  （ C）R　　　　　 （D）

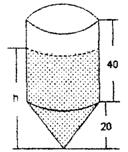
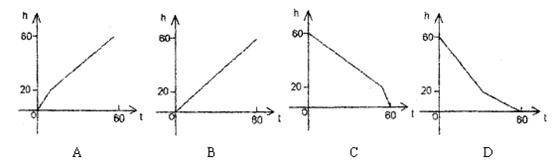
9.　　　 一个蓄水桶，60分钟可将一满桶水放干．其中，水位h（cm）随着放水时间t（分）的变化而变化．h与t的函数的大致图像为（ * ）

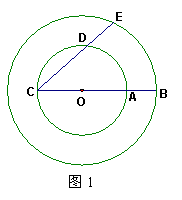
10.　 如图1，过两同心圆的小圆上任一点C分别作小圆的直径CA和非直径的弦CD，延长CA和CD与大圆分别交于点B、E，则下列结论中正确的是（ * ）

 （A）且 （B）且

 （C）且（D）且

二、填空题 （共6小题，每小题3分，满分18分）

11.　 分解因式：4－b²＝__________ * _____ .

12.　 方程组的解为　　  * 　　　　　  

13.　 已知:如图2,AB为⊙O 的直径,以AO、BO为直径作⊙O₁、⊙O₂，⊙O的弦 MN与⊙O1、⊙O2相切于C、D两点，AB=4cm，则图中阴影部分的面积是　　　 * 　　　　  cm²

14.　 已知为实数,且,则的值为　　 * 　　　  .

15.  如图3，已知ABCD为正方形，E、F分别为CD、CB延长线上的点，

且DE＝BF，请写出关于边和角的三个正确结论（不包括正方形的边和角）：

① 　　　 * 　　  ② 　　　* 　　　　 ③ 　　　 * 　　.

16.  设n为正整数，用科学计算器探究得出 与的大小关系为　　　　  .

三、解答题 (共9小题，满分102分，解答应写出文字说明、演算步骤或证明过程)

17.   (本小题满分9分) 解不等式组，并在数轴上将其解集表示出来.

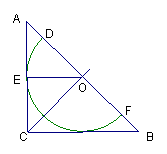
18.  (本小题满分9分) 某玩具厂有一批等腰直角三角形的余料(如图4),现准备将它加工后用作玩具上的装饰.要求将它截成半圆,该半圆的圆心在斜边上,且与两直角边都相切.

(1)  作出该半圆.(,保留作图痕迹，不写作法).

(2) 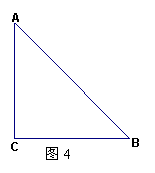 若等腰直角三角形的一条直角边AC=10cm,求所作半圆的半径.

19. 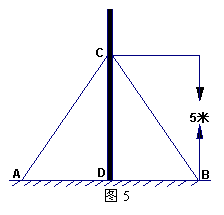 (本小题满分10分)如图5，在离地面高度5米处引拉线固定电线杆（电线杆与地面垂直），拉线AC的长6.18米，

（1）　　　 求拉线与地面所成的角∠CAD的大小（精确到1）；

（2）　　　 求点A与杆底D的距离AD（精确到0.01米）.

20.  (本小题满分12分) 改革开放以来，番禺的路桥得到空前发展，为番禺的经济腾飞奠定了基础。为了了解番禺某大桥的汽车流量,某班学生作了一些调查,他们分成五个小组,,这五个小组分别于五个时段进行统计，每个小组都分别进行两次了统计，，每次调查统计的时间为10分钟，数据如下：

组别	第一次调查（10分钟通过该大桥的汽车数量）	第二次调查（10分钟通过该大桥的汽车数量）
第一组	502辆	587辆
第二组	581辆	540辆
第三组	473辆	507辆
第四组	582辆	428辆
第五组	244辆	306辆

（1）　　　 利用样本平均数推测一天（24小时）通过该大桥的汽车数量为多少辆？

（2）　　　 若该大桥10年前平均每天的汽车流量为3万辆，问平均每天通过该大桥的汽车流量,在这10年内每5年的平均增长率是多少？（结果精确到1%）

21.  （本小题满分12分）已知一个反比例函数和一个一次函数的图象都经过点A（1，4）和点B（―2，―2），

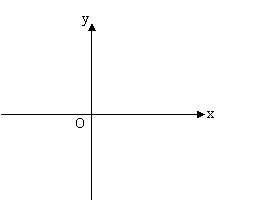　　（1）求反比例函数和一次函数的解析式，并在下面的坐标系中画出它们的图象.

　　（2）求△OAB的面积(O为坐标原点).

22.   (本题满分12分)已知：如图6，直线EC经过⊙O的圆心，分别交⊙O于B、C两点，直线EM与⊙O相切于点A，CD⊥EM于点D，交⊙O于点F.

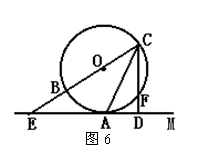求证：（1）∠ECA=∠ACD； （2）CA²=CE·CF.

23.  (本小题满分12分)某电信局现有600个已申请装机的ADSL用户，此外每天还有新申请的用户也待装机．设每天新申请装机的用户数量相同，每个安装小组每天装机的数量也相同．若安排3个安装小组，则60天可装完所有待装用户；若安排5个安装小组，则20天可装完所有待装用户．

　　（1）求该电信局每天新申请安装ADSL的用户数；

　　（2）如果要在5天内装完所有待装用户，那么电信局至少需安排几个安装小组同时安装?

24.  (本小题满分13分) 如图7,将边长为4的正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G.

(1)　若点M为CD的中点时,求CMG的周长；

(2) 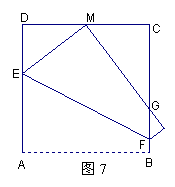 如果点M为CD上的任意一点(不含C、D两点),问CMG的周长是否与点M的位置有关?若有关,请将CMG的周长用含有DM的长的代数式表示;若无关,请说明理由.

25.  (本小题满分13分)

若二次函数y=x²-mx+2m-2 的图像与x轴的两个交点分别为A（x₁，0）和B（x₂，0）（x₁<x₂），顶点为C，

（1）若A、B两点间的距离为4，求实数m的值；

(2)  若ABC为钝角三角形,求满足题意的所有整数m的值.

初三数学综合练习 (一)参考答案及评分说明

四、选择题 （每小题3分，共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案	A	D	D	B	C	A	C	B	C	D

五、填空题 （共6小题，每小题3分，共18分）

11.　(2－b)(2+b)　12.  13.  14.  15. 答案不唯一,如CF=CE, ABF≌ADE,AF=AE,∠FAB=∠EAD, ∠FAE=∠AEF. ∠CFE=∠CEF=45⁰………，

16. 当时，，当时，. 如学生填写 不扣分.

说明：第12题没有写成组的形式，即写成，者扣1分，第13题等价的近似答案如0.429或0.43也可以.第14题出现和－2者扣1分.第15题每填对一个得1分.第16题没有带等号者扣1分.

六、解答题

17. 解：由（1）（2分）得（3分），由（2）得 （5分），（6分），因此，原不等式的解集为 （7分） 将其解集在数轴表示出来（略）.（9分）.

说明：其解集在数轴上表示错误的扣1-2分. 如空心、实心弄错等.

18.（1）如图弧为所作的半圆.图形正确 (3分) 有作图痕迹者（5分）.

（2）由于ABC为等腰直角三角形，则点O为AB中点，E为AC中点（7分），

因此所作半圆的半径为OE=BC=5（cm）（9分）

说明:作图痕迹可多样，如半圆圆心可为C的平分线与AB的交点，也可是AB的中点等.

 19. 解：（1）在RtADC中，（3分）=，（5分）.

（2）由于（7分）=（米）（9分），或由三角函数得出答：略（10分）

说明：不一定要有答，但要有表示回答题目问题的结束语.否则扣1分.精确度不正确者每处扣1分.

20.（1）先求10次调查的平均值 ：=475（3分）

即该大桥每10分钟通过的汽车数为475辆，则估计一天的汽车流量为（辆）（6分）

（2）设每5年的日汽车流量的平均增长率为x（7分），则（9分），解之得（11分）答：（略）（12分）

说明：如果第1问结果错误，第（2）问按第一问结果计算正确者第2问可以给4分.

21.（1）设反比例函数和一次函数的解析式分别为和（1分），将点A（1，4）和点B（）代入得 ，，，（2分）解之得，（5分）

故所求反比例函数为，一次函数为（6分）画出图像（略）（8分）

（2）由于一次函数于y轴的交点为C（0，2），（9分）

则△OAB的面积=△OAC的面积+△OCB的面积(10分)=(12分).

说明:第1问中将反比例函数与一次函数中的待定常数设为同一个字母者要扣分.本题解法多,可以按x轴分成两个三角形,也可以过点A作y轴的平行线,过点B作x轴的平行线,两平行线相交，利用图形的特点求解也可.

22.证明: (1) 连结AB,由于BC为⊙O的直径，则AB⊥AC，∴∠ABC+∠ACB=90⁰（2分），由于直线EM与⊙O相切于点A，则∠CAD=∠ABC，∴∠CAD+∠ACB=90⁰（4分），而CD⊥EM于点D，∴∠CAD+∠ACD=90⁰（5分），因此∠ACB=∠ACD，即∠ECA=∠ACD（6分）

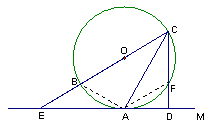
(2)连接AF，则由于EM与⊙O相切于点A，则∠CAE=∠CFA(8分)

由（1）知∠ECA=∠ACF ∴ACF∽ECA(10分)，(11分)，即CA²=CE·CF(12分).

说明:本题解法多，如第1问还可以连结AO，利用AO与CD平行也可得出等.

23. 解：（1）设每天新申请装机的用户数为x个，每个小组每天安装y户(2分)　　　　

　　依题意，有　(4分)　　　　　解得　(6分)　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　（2）设需安排a个小组同时安装(7分)，则　600＋5×20≤5×10a (10分)　a≥14(11分)．　　　　　　　　　　　　　　　　　　　　　　　　　　　

答：每天新申请装机用户为20个,每个小组每天安装10户,至少需安排14个安装小组同时安装(12分).

24. 解：（1）设DE=a,则EA=EM=4-a(1分) 由于DM=2则由勾股定理得(2分),解得(3分),由CMG∽DEM得,,CG=(4分),由勾股定理得MG=,因此CMG的周长为8 (6分).

(当然也可以根据相似三角形的周长比等于相似比来解)

(2)设DM=x,DE=b,则EM=4-b(8分),由勾股定理得(9分),解得 (10分),而CMG∽DEM,则它们的周长之比等于相似比,由于DEM的周长为4+x, 设CMG的周长为y,则(11分),则(12分)为定值，与DM的长无关系.(13分)

说明：本题第（2）问计算方法多，应根据学生的解题过程给分。

25. 解: (1) 显然,是方程x²-mx+2m-2=0的两根(1分), 则,（3分）

由于A、B两点间的距离为4，即,则（4分）,即（5分）,所以,解之得,因此,（6分）.

(2) 由于C为抛物线的顶点，则AC=BC，若ΔABC为钝角三角形，则只能是∠C为钝角(7分)，则点C在以AB为直径的圆内，即点C到轴的距离小于AB长度的一半(7分),而点C的坐标为,即为C（8分）所以点C到x轴的距离为,而AB=（9分）,

因此  (10分)

当时，，即，，即，而为整数，则(11分)

当时，，即，，即，而为整数，则(12分)

当时，显然不符合题意,因此，所求的值为1或3　(13分)

说明：（1）第1问也可由及求出再代入即可。

（2）第2问的值也可通过计算器辅助解决.如当时，.由探索出得出…，同样可以讨论的情况.

　　　　　　　　　　　　　　　　　　　　　　　

以上答案只列出一种解法,对其它解法,请另制订评分说明,错误难免,请批评指正!