初中学业水平模拟数学测试卷(三)

初中学业水平模拟数学测试卷(三)

数 学 试 题

一、选择题(每小题4分，共40分)

1、下列计算正确的是……………………………………………………………………【　　 】

A.　　 B.　　 C.　　 D.

2、据测算，我国每年因土地沙漠化造成的经济损失为547.5亿元，用科学记数法表示我国一年因土地沙漠化造成的经济损失为…………………………………………………【　　 】

A.5.475×10¹⁰（元）　 B.5.475×10¹¹ （元）　 C.54.75×10¹⁰（元）　 D.54.75×10¹¹（元）

3、下面的4幅图中，经过折叠不能围成一个立体图的一幅是………………………【　　 】

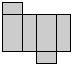A　　　　　　  B 　　　　　　　　 C　　　　　　　  　D

4、如图，在△ABC中，∠ACB＝90°，∠B＝30°，AD是角平分线，DE⊥AB于E，AD、CE交于G，则图中共有等腰三角形…………………………………………………【　　 】

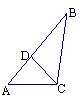A.1个　　 B.2个　　 C.3个　　 D.4个

(第4题图)　　　　　  (第5题图)　　　　　　　　　　　　　  (第8题图)

5、在△ABC中，D为AC边上一点，∠DCB=∠A，BC=，AB=3，则BD的长为【　　 】

A.1　　 B.　　 C.2 　　 D.

6、抛物线y=ax²+bx+c(a≠0)(a≠0)的顶点坐标是(2，－1)，则b+c的值等于……【　　 】

A.-1　　 B.-2　　 C.2　　 D.1

7、小明参加军训，10次射击训练的结果如下表所示：

命中环数	5	6	7	8	10
命中次数	1	2	2	4	1

他利用所学的统计知识对自己的射击成绩进行了评估，其中错误的是……………【　　 】

A.平均数是(10＋8×4＋7×2＋6×2＋5)÷10＝7.3（环）

B.众数是8（环），打8环的次数占40％

C.中位数是8（环），比平均数高0.7（环）

D.方差是1.81，稳定性一般

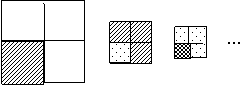
8、小王将一张正方形纸片撕成四张后，取其中一张载撕成四张，又取其四张中的一张在撕成四张，……，如此继续，在下面给出的四组数据中，哪一个是小王经过若干次撕纸后撕成的碎纸片数………………………………………………………………………………【　　 】

A.2002　　 B.2003　　 C.2004　　 D.2006

9、某品牌手机为了打开市场,促进销售,准备对其特定型号的产品降价,有四种降价方案:①先降价a%，再降价b%；②先降价,再降价a%；③先降价，再降价；④一次性降价(a+b)%。其中a>b，则最终降价幅度最小的方案是………………【　　 】

A.①　　 B.②　　 C.③　　 D.④

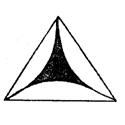10、如图所示，共产品的商标由三个半径都等于R的半圆两两外切得到的图形的一部分，则切点问的弧所围成的阴影部分的面积是…………………………………………【　　 】

A.　　 B.

C.　　　 D.

二、填空题(每小题4分，共40分)

11、小明和小强玩掷骰子游戏，一次抛掷2枚骰子，点数之和大者为胜，小强先掷，掷出2点，轮到小明时，小明取胜的概率是　　　 .

12、将一个四边形的纸片一刀剪去一个角后，所得的多边形的内角之和是　　　　　  ；

13、若一个圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的圆心角的度数是　　 .

14.函数y₁=k₁x₁的图象通过P（2，3）点，且与函数y₂=k₂x₂的图象关于y轴对称，那么它们的解析式y₁=　　　，y₂=　　　.

15、等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，△A₁B₁C₁的各边与它的内切圆相切于A₂，B₂，C₂，…，以此类推.若△ABC的面积为1，则△A₅B₅C₅的面积为　　　　．

三、(每小题8分，共16分)

16、先化简：，再取一个合理的值代入求值.

17.解不等式组：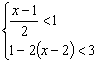

四、(每小题9分，共18分)

18.某电信局现有600个已申请装机的ADSL用户，此外每天还有新申请的用户也待装机．设每天新申请装机的用户数量相同，每个安装小组每天装机的数量也相同．若安排3个安装小组，则60天可装完所有待装用户；若安排5个安装小组，则20天可装完所有待装用户．

(1)求该电信局每天新申请安装ADSL的用户数；

(2)如果要在5天内装完所有待装用户，那么电信局至少需安排几个安装小组同时安装?

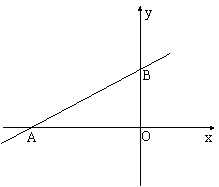19.设一次函数y=x+2的图像为直线l，l与x轴、y轴分别交于点A、B.

(1)求tan∠BAO的值

(2)直线m经过点P(－3，0)，若直线l、m与x轴围成的三角形与直线l、m与y轴围成的三角形相似，求直线m的解析式

五、(每小题4分，共40分)

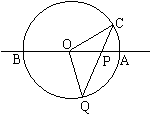20.如图，直线AB经过圆O的圆心，且于圆O相交于A、B两点，点C在圆O上且∠AOC=30⁰，点P为直线AB上一动点（与点O不重合），直线PC与圆O相交于点Q，是否存在点P，使得QP=QO，如果存在，那么这样的点P共有几个？并相应求出∠OCP的大小；如果不存在，请说明理由。

21.平行四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.

(1)如图1，P是□ABCD内任意一点，连结PA、PB、PC、PD。试探索相对的两对三角形：△PAB、△PCD与△PBC、△PAD面积之间的数量关系.

(2)如图2，P是矩形ABCD内一点，S_△PAB=5，S_△PBC=12，求S_△PBD.

六、(本题满分12分)

22.某电脑软件经销店，以每件30元的进价购进一种新开发的软件W,通常销售利润可达到进价的60%.为促进商店内与软件W相关联的其它软件(销售价格不变)的销售，决定将软件W在不赔本的情况下,每件的销售利润以不高于进价30%的可变价格出售，用来招揽顾客.经过几天销售发现，其它软件日均销售利润元与软件W的售价x元满足一次函数关系，当软件W的售价分别是33元和38元时，其它软件的销售利润分别是188元和168元.

(1)求出y与x的函数关系式，并写出的取值范围；

(2)若在一天中，能将19件软件W售出，销售软件W与销售其他软件的利润和不低于230元，试确定软件W的售价范围.（利润＝售价—进价）.

七、(本题满分12分)

23.如图，将边长为4的正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G..

(1)若点M为CD的中点时,求CMG的周长；

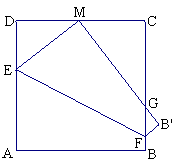(2)如果点M为CD上的任意一点(不含C、D两点),问CMG的周长是否与点M的位置有关?若有关,请将CMG的周长用含有DM的长的代数式表示;若无关,请说明理由.

八、(本题满分12分)

24.在平面直角坐标系中给定以下五个点A（-2，0）、B（1，0）、C（4，0）、D（-2，）、E（0，-6），从这五个点中选取三点，使经过三点的抛物线满足以轴的平行线为对称轴。我们约定经过A、B、E三点的抛物线表示为抛物线ABE。

(1)符合条件的抛物线共有多少条？不求解析式，请用约定的方法一一表示出来；

(2)在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点，玩摸球游戏，每次摸三个球。请问：摸一次，三球代表的点恰好能确定一条符合条件的抛物线的概率是多少？

(3)小强、小亮用上面的五球玩游戏，符合要求的抛物线开口向上，小强可以得1分；抛物线开口向下小亮得5分，你认为这个游戏对两人公平吗？说说你的理由。