新课标(北师大版)中考数学第一轮复习测试卷
第八单元 概率
一、选择题(每小题4分，共40分)
1、下列事件中，确定事件是（ D ）
A.掷一枚六个面分别标有1~6的数字的均匀骰子，骰子停止转动后偶数点朝上
B.从一副扑克牌中任意抽出一张牌，花色是红桃
C.任意选择电视的某一频道，正在播放动画片
D.在同一年出生的367名学生中，至少有两人的生日是同一天。
2、某商店举办有奖销售活动，购物满100元者发对奖券一张。在10000张奖券中，设特等奖1个，一等奖10个，二等奖100个。若某人购物刚好满100元，那么他中一等奖的概率是（ B ）
A.
B.
C.
D.
3、一套书共有上、中、下三册，将它们整齐的摆放在书架上，恰好摆成“上、中、下”顺序的概率是（ D ）
A.
B.
C.
D.
4、下列说法中正确的是 ( B )
A.投掷一枚图钉，针尖朝上、朝下的概率一样
B.投掷一枚均匀的硬币，正面朝上的概率是
C.统一发票有“中奖”与“不中奖”二种情形，所以中奖的概率是
D.投掷一粒均匀骰子，每一种点数出现的机率都是
，所以每投六次，必须出现一次“1点”
5、设甲投掷一个一元硬币，乙投掷两个一元硬币，则乙投掷均为正面的概率和甲投掷出现正面的概率之比是（ C ）
A. B.
C. D.
6、两个袋中各装有一只白球和一只黑球，从第一个袋中任取一球，记下颜色后再放入第二个袋中，搅匀后再从第二个袋中任取一球，那么两次取出的球有相同颜色的球的概率是（ B ）
A.
B.
C.
D.
7、甲、乙两人玩掷骰子的游戏，共有两枚骰子，以两人掷得两枚骰子之和的大者获胜，若甲掷得两枚骰子数字之和为8，那么这场游戏乙获胜的概率是（ C ）
A.
B.
C.
D.
8、30张牌，牌面朝下，每次抽一张出来计下花色再放下洗牌后再抽，抽到红桃、黑桃、梅花、方片的频率依次为20%、32%、45%、3%，下面对四种花色的牌数估计正确的是（ C ）
A.红桃6张，梅花10张，黑桃13张，方片1张
B.红桃6张，黑桃10张，方片13张，梅花1张
C.红桃6张，黑桃10张，梅花13张，方片1张
D.黑桃6张，红桃10张，梅花13张，方片1张
9、现有10张卡片，分别写有0至9十个数字，任意抽出两张，能组成18的概率是（ C ）
A.
B.
C.
D.
10、如图每个转盘被分成若干相同的扇形，用其中两个转盘做“配紫色”游戏。其中获胜概率最高的两个转盘是（ D ）
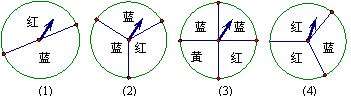
A.(1)与(2) B.(2)与(3) C.(3)与(4) D.(2)与(4)
二、填空题(每小题4分，共40分)
11、某校九年级(3)班在体育毕业考试中，全班所有的学生得分的情况如下表所示：
| 分数段 | 18分以下 | 18~20分 | 21~23分 | 24~26分 | 27~29分 | 30分 |
| 人数 | 2 | 3 | 12 | 20 | 18 | 10 |
那么随机地抽取1人，恰好是获得30分的学生的概率是 
.
12、有两组相同的纸牌，每组两张，他们的牌面数字分别是2和3，从每组牌中各摸出一张称为一次实验，估计两张牌的牌面数字和为偶数的概率为 
.
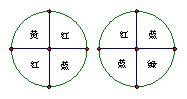
13、下图是“配紫色”游戏的两个转盘，转盘停下后两个转盘的指针所指颜色能配成紫色的概率是 
.
14、在一个不透明的袋中装有除颜色外其余都相同的3个小球，其中一个红球、两个黄球.如果第一次先从袋中摸出一个球后不再放回，第二次再从袋中摸出一个，那么两次都摸到黄球的概率是 
.
15、有两张同样大小的正方形纸片，分别画有不同图案，把每张纸片都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图案的概率是 .
三、(每小题8分，共16分)
16、设计一个方案，模拟“掷一枚均匀硬币”实验，估计正面朝上的概率.
(1)请采用计算器模拟掷币实验，并简要说明步骤
(2)如果没有计算器，我们可以用两张扑克(1张黑桃，1张红桃)代替，分别代表硬币的正面与反面。你还能想出其他什么替代物吗？请把你能想到的替代物填入下表
| 问题中的实物 | 模拟实验中的替代物 | ||
| 1 | 2 | 3 | |
| 一枚均匀硬币 | 两张扑克， “黑桃”代表“正面” “红桃”代表“反面” | ||
17、现有三个布袋，里面放着一些已经搅匀了的小球，具体的数目如下表所示.
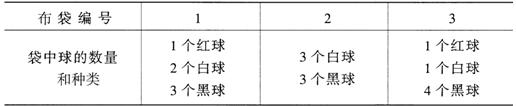
（1）随机地从第一个口袋中取出一个球，求这个球是白色的概率；
（2）随机地从第二个口袋中取出两个球，求这两个球都是白色的概率；
（3）随机地从三个口袋中各取出一个球，求取出的三个球的颜色都是白色的概率.
四、(每小题9分，共18分)
18、如图，用树状图或表格求两个转盘“配紫色”的概率.
19、小明和小亮玩“石头、剪子、布”的游戏，假定两人是等可能地采取石头、剪子、布三个策略，那么一个回合不能决定胜负的概率是多少？
五、(每小题10分，共20分)
20、小明和小亮一起玩各抛一个普通正方体骰子的游戏.
(1)指出游戏中的必然事件，不可能事件和随机事件各一个；
(2)如果两个骰子上的点数之积为奇数，小明胜；如果点数之积为偶数，则小亮胜。你认为这个游戏公平吗？如果不公平，谁获胜的概率大？请说明理由.
(1)必然事件：两个骰子上的点数之和大于1或小于13的整数；不可能事件：两个骰子上的点数只和为1或大于12的数；随机事件：两个骰子上的点数之和为奇数(或偶数) (2)不公平。因为P(小明获胜)=
，p(小亮获胜)=
.
21、做抛掷两枚硬币的实验，在对实验数据整理的过程中，某个不确定事件出现的频率随实验次数变化折线图如图所示：
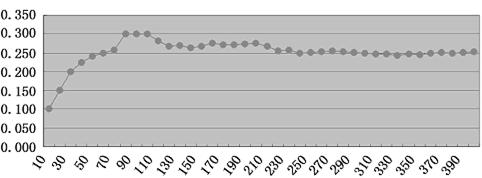
(1)这个图形中的折线变化特点说明了什么？
(2)请你说出在该实验中符合折线变化特点的一个不确定事件；
(3)如果小明邀请你玩一个抛掷两枚硬币的游戏，游戏规则这样：抛出两个正面——你赢1分；抛出其他结果——小明赢1分；谁先到10分，谁就得胜．你会和小明玩这个游戏吗？这个游戏规则对你和小明公平吗？
六、(本题12分)
22、袋中装有编号为1、2、3的三个形状大小相同的小球，从袋中随意摸出1球。并且随意抛掷一个面上标有1，2，3，4，5，6各一数字的正方体均匀骰子。
（1）如果摸出1号球和骰子朝上的数字为1则甲胜；如果摸出2号球和骰子朝上的数字为2，则乙胜。这个游戏对双方公平吗？
（2）如果摸出的球编号为奇数和骰子朝上的数字为奇数则甲胜；如果摸出的球编号为偶数和木块朝上的数字为偶数，则乙胜。这个游戏对双方公平吗？说明理由。
①公平 获胜概率相同
②不公平；因为甲获胜概率为，乙获胜概率为
七、(本题12分)
23、有一个转盘游戏，转盘平均分成10份（如图），分别标有1、2、……、10这十个数字，转盘上有固定的指针，转动转盘，当转盘停止转动时，指针指向的数字即为转出的数字．两人进行游戏，一人转动转盘，另一人猜数，如果猜的数与转出的数情况相符，则猜数的人获胜，否则转盘的人获胜．猜数的方法为下列三种中的一种：
(1)奇数或偶数；
(2)猜是3的倍数或不是3的倍数；
(3)猜大于4的数或不大于4的数．
如果你是猜数的游戏者，为了尽可能取胜，你选哪种猜法？怎样猜？
 |
八、(本题12分)
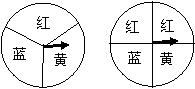
24、某商场在“五一”期间进行促销活动，凡购物满50元均可参加转转盘返购物券的活动，每50元可转动一次，所得购物券可以在本商场中继续消费，转盘共有两种，如图所示。活动规定：
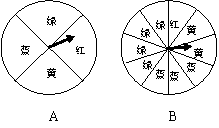①转盘A(转盘A被等分成4份)中指针转到红色区域可返回50元购物券，转到黄色区域可返还20元购物券，转到蓝色区域可返还10元购物券，转到绿色区域无购物券返还.
②转盘B(转盘B被等分成10份)中指针转到红色区域可返回100元购物券，转到黄色区域可返还30元购物券，转到蓝色区域可返还10元购物券，转到绿色区域无购物券返还.
(1)请你分别计算转盘A和转盘B平均每转动一次转盘可以返还多少元的购物券？
(2)你若在此商场消费，你选择转动转盘A还是转动转盘B，请说明里选择的理由.
(3)小明在商场购买了一个400元的随身听，他选择转动转盘A，那么从理论上来说，他应该能够得到多少元的购物券？
(1)转动一次转盘A平均可得购物券：50×25%+20×25%+10×25%=20(元)，每转动一次转盘B平均可得购物券：100×10%+3020%+10×30%=19(元) (2)选择转动转盘A更为合算 (3)400÷50×20=160(元)，因此理论上应能得到160元购物券.