新课标(北师大版)中考数学第一轮复习测试卷
第十五单元 直角三角形的边角关系
一、选择题(每小题4分，共40分)
1、在△ABC中，∠C=90°，AB=13，BC=12，则cosA的值为（ B ）
A.
B.
C.
D.
2、在Rt△ABC中，∠C=90°，AC=6，sinB=
，那么AB的长是（ A ）
A.4 B.9 C.3
D.2
3、在△ABC中，∠C＝90°，cosA=
，那么tanA等于（ D ）
A.
B.
C.
D.
4、在△ABC中，∠C＝90°，AC＝BC，则sinA的值等于（ B ）
A.
B.
C.
D.1
5、在Rt△ABC中，如果各边长度都扩大为原来的2倍，那么锐角A的正弦值（ D ）
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
6、某人沿着倾斜角α为的斜坡前进了100米，则他上升的最大高度是（ B ）
A.
米
B.100sinα米 C.
米
D.100cosα米
7、如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于（ B ）
A.1 B.
C.
D.
(第7题图) (第8题图) (第9题图) (第10题图)
8、如图，CD是平面镜，光线从A出发经CD上点E发射后照射到B点。若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=11则tanα的值为（ D ）
A.
B.
C.
D.
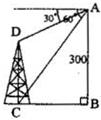
9、如图，在300m高的峭壁上测得一塔的塔顶与塔基的俯角分别为30°和60°，则塔高CD为（ A ）
A.200m B.180m C.150m D.100m
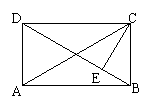
10、如图，在矩形ABCD中，CE⊥BD于点E，BE=2，DE=8，则tan∠ACE的值为（ C ）
A.
B.
C.
D.2
二、填空题(每小题4分，共20分)
11、计算：
= 
-1 .
12、已知∠α为锐角，且sinα=，则cosα= 
.
13、在△ABC中，∠C＝90°，如果AB＝4，那么cosA=，那么BC的长为 2 .
14、甲乙两楼相距60米，从乙楼底部看甲楼顶部的仰角为45°，从甲楼的顶部看乙楼的顶部俯角为30°，则乙楼的高为__60-20_________米.
15、某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转．某一指令规定：机器人先向正前方行走１米，然后左转45°.若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了 8 米．
三、(每小题8分，共16分)
16、如图，在Rt△ABC中，∠C=90°，AC=6，∠A的平分线AD=4，求∠B的度数及边BC、AB的长.
∠B=30°，AB=12，BC=6
17、在△ABC中，∠A、∠B都是锐角，且sinA=，tanB=
，AB=10，求△ABC的面积.
四、(每小题9分，共18分)
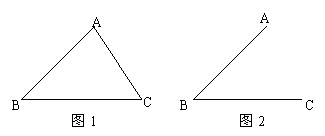
18、(1)如图1，在△ABC 中，∠B 、∠C 均为锐角，其对边分别为b、c，求证：
=
.
(2)在△ABC 中，AB=，AC=，∠B =45°，问满足这样的△ABC 有几个？请在图2中作出来(不写作法，不述理由)，并利用(1)的结论求出∠ACB的大小。
 |
略
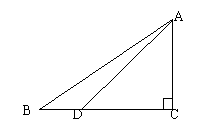19、如图，在Rt△ABC中，∠C=90°，sinB=
，点D在BC边上，且∠ADC=45°，DC=6，求tan∠BAD。
五、(每小题10分，共20分)
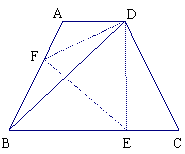20、如图，等腰梯形ABCD中，AD∥BC，∠DBC=45°。翻折梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于点F、E。若AD=2，BC=8.
求：(1)BE的长；
(2)∠CDE的正切值.
(1)BE=5 (2)tanCDE=
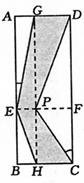21、如图，从一块矩形薄板ABCD上裁下一个工件GEHCPD（阴影部分）. 图中EF//BC，GH//AB，∠AEG=11°18′，∠PCF=33°42′，AG=2cm，FC=6cm. 求工件GEHCPD的面积(参考数据：
).
工件GEHCPD的面积约为48cm2.
六、(本题12分)
22、居民楼的采光是人们购买楼房时关心的一个重要问题。冬至是一年中太阳相对地球北半球位置最低的时刻，只要此时楼房的最低层能菜刀阳光，一年四季整座楼均能受到阳光的照射。某地区冬至时阳光与地面所成的角约为30°，如图所示。现有A、B、C、D四种设计方案提供的居民楼的高H(米)与楼间距L(米)的数据，如下表所示。仅就图中居民楼乙的采光问题，你认为哪种方案设计较为合理，并说明理由(参考数据=1.732)
| A | B | C | D | |
| H(米) | 12 | 15 | 16 | 18 |
| L(米) | 18 | 25 | 28 | 30 |
根据题意：tan30°=
=
=0.5773，设计合理的楼房应满足：≤0.5773，∵对于A方案：
=0.6667>0.5773，对于B方案：
=0.6>0.5773，对于C方案：
=0.5714<0.5773，对于D方案：
=0.6>0.5773.∴C方案较为合理.
七、(本题12分)
23、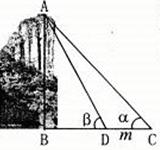
“玉女峰”是武夷山最秀丽的山峰，她亭亭玉立于九曲溪边。如图，为测得峰顶A到河面B的高度h，当游船行至C处时测得峰顶A的仰角为α，前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
(1)用含α、β和m的式子表示h ；
(2)当α=48°，β=66°，m=50米时，求h的值.(精确到1米)
(1)h=
(2)110米
八、(本题12分)
24、一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？
 |
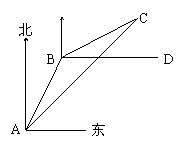这艘渔船没有进入养殖场的危险