新课标(北师大版)中考数学第一轮复习测试卷
第十一单元 四边形的认识与证明
一、选择题(每小题4分，共40分)
1、下列命题中正确的是（ D ）
A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是菱形
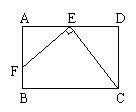
2、如图，矩形ABCD中，E在AD上，且EF⊥EC，EF=EC，DE=2，矩形的周长为16，则AE的长为（ A ）
A.3
B.4
C.5 D.7
 | |||
 | |||
(第2题图) (第3题图) (第4题图) (第5题图)
3、如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF等于（ D ）
A.80° B.70° C.65° D.60°
4、如图是用4个相同的小矩形和1个正方形镶嵌而成的正方形图案。已知该正方形图案的面积为49，小正方形的面积围，若用xy表示小矩形的两边长(x>y)，请观察图案，指出以下关系式中不正确的是（ D ）
A.x+y=7 B.x-y=2 C.4xy+4=49 D.x2+y2=25
5、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝，点E，F，G，H分别是四边形ABCD各边的中点.其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均不计余料）.若生产这批风筝需要甲布料30匹，那么需要乙布料（ C ）
A．15匹 B．20匹 C．30匹 D．60匹
6、如图，在等腰梯形ABCD中，AB∥CD，AD=BC，∠A=60°，AB=9，CD=5，则BC的长是（ B ）
A．3 B．4 C．5 D．6
7、在一个四边形ABCD中，依次连结各边中点的四边形是菱形，则对角线AC与BD需要满足条件（ B ）
A. 垂直 B. 相等 C.垂直且相等 D. 不再需要条件
8、在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是 （ D ）
 |  |  |  |
A. B. C. D.
9、边长相等的下列两种正多边形的组合，不能作平面镶嵌的是（ B ）
A.正方形与正三角形 B.正五边形与正三角形
C.正六边形与正三角形 D.正八边形与正方形
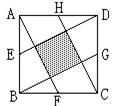10、如图，E，F，G，H分别是正方形ABCD各边的中点，要使中间阴影部分小正方形的面积是5，那么大正方形的边长应该是（ C ）
A.
B.
C.5 D.
二、填空题(每小题4分，共20分)
11、在□ABCD中，AB=4cm，AD=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF= 3 cm.
(第11题图) (第12题图) (第13题图)
12、如图，一张矩形纸片，要折叠出一个最大的正方形.小明把矩形的一个角沿折痕AE翻折上去，使AB和AD边上的AF重合，则四边形ABEF就是一个最大的正方形.他的判定方法是____有一组邻边相等的矩形是正方形等________________________________.
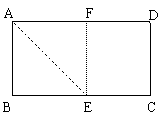
13、如图，在长方形ABCD中，AB=3，BC=2，E为BC的中点，F在AB上，且BF=2AF，则四边形AFEC的面积为 2 .
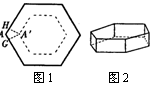
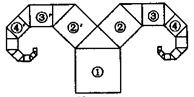14、将一块正六边形硬纸片(如图1)，做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面，如图2)，需在每一个顶点处剪去一个四边形，例如图1中的四边形AGA/H，那么∠GA/H的大小是 60 度。
 |
(第11题图) (第12题图)
15、如图，是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②，…，依此类推，若正方形①的边长为64cm，则正方形⑦的边长为 8 cm.
三、(每小题8分，共16分)
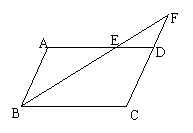
16、已知：如图，四边形AEFD和四边形EBCF都是平行四边形.
求证：△ABE≌△DCF.
证明略
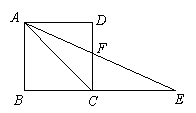17、如图，在正方形ABCD的边BC的延长线上取一点E，使CE=CA，AE与CD交于F点．求∠AFC的度数．
112.5°
四、(每小题9分，共18分)
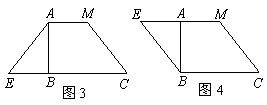
18、用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
 |
(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形，设原矩形纸片的周长为12厘米，试求出原矩形纸片的面积.
（1）
（2）由题可知AB＝CD＝AE，又BC＝BE＝AB＋AE
∴BC＝2AB
由题意知 AB+BC=6
∴AB=2，BC=4
∴S矩形=AB×BC=8
答：原矩形纸片的面积为8cm2.
19、已知：如图，四边形ABCD中，AB=DC，AC=BD，AD≠BC.
求证：四边形ABCD是等腰梯形.
证明略
五、(每小题10分，共20分)
20、已知：如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，MA=MC.
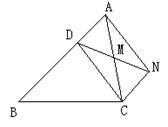求证：CD=AN.
证明略
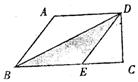21、如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点。将直角梯形沿对角线BD折叠，使△ABD与△EBD重合(如图中阴影部分)。若∠A=130°，AB=4cm，求梯形ABCD的高CD的长(结果精确到0.1cm).
略
六、(本题12分)
22、如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF＝CE．
（1）求证：四边形ACEF是平行四边形；
（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论；
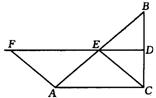（3）四边形ACEF有可能是正方形吗？为什么？
(1)证明略 (2)当∠B=30°时，四边形CEF是菱形.证明略 (3)四边形ACEF不可能是正方形.
七、(本题12分)
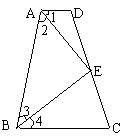
23、如图，四边形ABCD中，点E在边CD上，连结AE、BE.给出下列五个关系式：①AD∥BC；②DE＝CE；③∠1＝∠2；④∠3＝∠4；⑤AD＋BC＝AB.将其中的三个关系式作为题设，另外两个作为结论，构成一个命题.
(1)用序号写出一个真命题（书写形式如：如果×××，那么××）.并给出证明(6分)
(2)用序号再写出三个真命题(不要求证明)(6分)
(3)真命题不止以上四个，想一想，你还能多写出几个真命题(每多写出一个真命题就给你加1分，最多加2分).
(1)如果①②③，那么④⑤ 证明略 (2)如果①②④，那么③⑤；如果①③④，那么②⑤；如果①③⑤，那么②④ (3)如果(1)(2)中四个命题含假命题(“如果②③④，那么①⑤”)，则不加分；若(3)中含假命题，也不加分.
八、(本题满分12分)
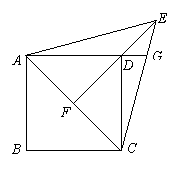
24、如图，在正方形ABCD中，以对角线AC为一边作一等边△ACE，连结ED并延长交AC于点F.
(1)求证：EF⊥AC；
(2)延长AD交CE于点G，试确定线段DG和线段DE的数量关系.
(1)证明：由已知,得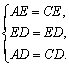
∴△AED≌△CED . ∴∠AED＝∠CED . 又∵△AEC为等边三角形,∴EF⊥AC .
（2）过G作GM⊥EF，垂足为M. 由已知和(1) ，得∠AED＝∠CED＝30o，∠EAD＝150 .
∴∠EDG＝45o . ∴MD＝GM .
设GM＝x,则DG＝
.在Rt△MEG中，EG＝2MG＝2x
, ∴EM＝
. ∴ED＝+x＝(
)x . ∴
.即DE＝
DG (或
).