初三数学练习题
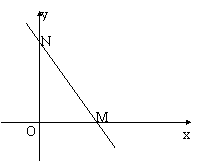
1、如图,直线![]() 与x轴、y轴分别交于点M、N,如果点P为坐标轴上上一点,则以点P为
与x轴、y轴分别交于点M、N,如果点P为坐标轴上上一点,则以点P为
 圆心,
圆心,![]() 为半径的圆与直线
为半径的圆与直线![]() 相切,求点P的坐标
相切,求点P的坐标
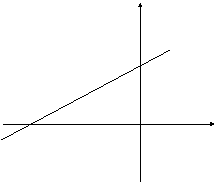
2、设一次函数![]() 的图像为直线l,l与x轴、y轴分别交于点A、B
的图像为直线l,l与x轴、y轴分别交于点A、B
⑴ 求tan∠BAO的值
|
|
|
|
|
 求直线m的解析式
求直线m的解析式
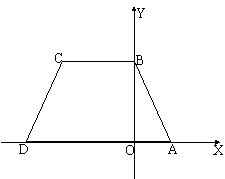
3、等腰梯形ABCD,AD//BC,AB=DC,面积S=9,建立如图的直角坐标系,已知A(1,0),B(0,3)
⑴ 求C、D两点的坐标; ⑵ 取点E(0,1)连接ED并延长交AB于F,说明:DF⊥AB
⑶ 将梯形ABCD绕A点旋转180°得到AB’C’D’,求对称轴平行于y轴,且经过A、B’、C’三点的
抛物线解析式
⑷ 是否存在这样的直线,满足以下条件:① 平分x轴,② 与⑶中抛物线有两交点,且这两交点和
 ⑶中抛物线顶点恰好是一个等边三角形的三个顶点?若存在,求出这个等边三角形的面积;若不
⑶中抛物线顶点恰好是一个等边三角形的三个顶点?若存在,求出这个等边三角形的面积;若不
存在,请说明理由
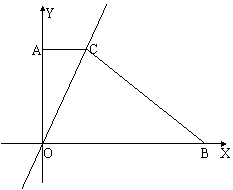
4、如图,在直角坐标系内的梯形AOBC中,AC//OB,AC、OB的长分为关于x的方程![]()
的两根,并且S△AOC:S△BOC=1:5
⑴ 求AC、OB的长; ⑵ 当BC⊥OC时,求OC的长及OC所在直线的解析式
⑶ 在第⑵问的条件下,线段OC上是否存在一点M,过M点作x轴的平行线交y轴于F,交BC于D,
 过点D作y轴的平行线,交x轴于E,使S矩形FOED=
过点D作y轴的平行线,交x轴于E,使S矩形FOED=![]() S梯形AOBC?若存在,请直接写出M点的坐标;
S梯形AOBC?若存在,请直接写出M点的坐标;
若不存在,请说明理由
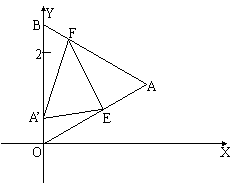
5、如图,△OAB是边长为![]() 的等边三角形,其中O是坐标原点,顶点B在y轴的正方向上,将
的等边三角形,其中O是坐标原点,顶点B在y轴的正方向上,将
△OAB折叠,使点A落在边OB上的A’点,折痕为EF
⑴ 求当A’E//x轴时,点A’和E的坐标;
⑵ 求当A’E//x轴,且抛物线![]() 经点A’和E时,该抛物线与x轴的交点坐标;
经点A’和E时,该抛物线与x轴的交点坐标;
⑶ 当点A’在OB上运动但不与点O、B重合时,△A’EF能否成为直角三角形?若能,请求出此时点A’
 的坐标;若不能,请说明理由
的坐标;若不能,请说明理由
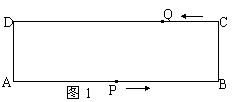
6、如图1,在矩形ABCD中,AB=20cm,BC=4cm,点P从A开始沿折线A-B-C-D以4cm/s的速
度移动,点Q从C开始沿CD边以1cm/s的速度移动。如果点P、Q分别从A、C同时出发,当其中
一点到达D时,另一点也随之停止运动,设运动时间为t s
⑴ 当t为何值时,四边形APQD为矩形?
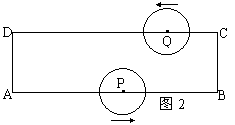
 ⑵ 如图2,如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
⑵ 如图2,如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
7、如图,在直角梯形ABCD中,AD//BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为
⊙O的直径,动点P沿AD方向从点A开始向点D以1cm/s的速度运动,动点Q沿CB方向从点C
开始向点B以2cm/s的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点
也随之停止运动
⑴ 求⊙O的直径;
⑵ 求四边形PQCD的面积y关于P、Q运动时间t的函数关系式,并求四边形PQCD为等腰梯形时,
四边形PQCD的面积;
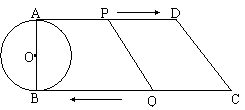 ⑶ 是否存在某一时刻t,直线PQ与⊙O相切?若存在,求出t的值;若不存在,请说明理由
⑶ 是否存在某一时刻t,直线PQ与⊙O相切?若存在,求出t的值;若不存在,请说明理由
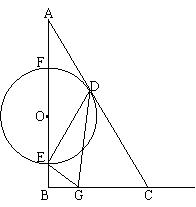
8、如图,已知Rt△ABC中,∠B=90°,∠A=30°,BC=6cm,点O从A点出发,沿AB以每秒![]() cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点,过点E作EG⊥DE交射线BC于点G
cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点,过点E作EG⊥DE交射线BC于点G
⑴ 若E与B不重合,当t为何值时,△BEG与△DEG相似?
⑵ 当t在什么范围内时,点G在线段BC上?当t在什么范围内时,点G在线段BC的延长线上?
 ⑶ 当点G在线段BC上(但不在端点B、C)时,求四边形CDEG的面积S(cm2)关于时间t(秒)的函数关系式,并求当点O运动了几秒钟时,S取得最大值,最大值为多少?
⑶ 当点G在线段BC上(但不在端点B、C)时,求四边形CDEG的面积S(cm2)关于时间t(秒)的函数关系式,并求当点O运动了几秒钟时,S取得最大值,最大值为多少?