初三数学模拟测试（3）

初三数学模拟测试（3）

 （满分150分，考试时间：120分）

　 班学号　　姓名　　  成绩　　

一、选择题：每题四个选项中，只有一个是正确的，请将选项前的字母符号填入下表相应表（本大题共17小题，每小题3分，共51分）

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
答案

1、下列运算正确的是　　　　  　(　　　).

（A）.x³·x²=x⁶　（B）2a+3b=5ab　（C）.(a+1)²=a²+1　（D）

2、如果两圆只有两条公切线,那么这两圆的位置关系是　　  (　　　 ).

（A）.内切　　  （B）.外切　　　（C）.相交　　　　  （D） .外离

3、分式的值为0,则x的取值为　　　 (　　　 ).

（A）　　　（B）　 （C）或　　（D）或

4、计算所得的结果是（　　　 ）

(A)、4　　　　 　(B)、 2　　 　　（C）、3　　　　　 （D）、1

5、下列二次根式中，最简二次根式是(　　　 )．

(A)、　　　 　(B)、　　　　(C)、 　　　　 (D)、

6、已知关x的方程x²－3x＋m＝0的一个根是另一个根的2倍，则m的值为（　　　）

A、2　　　　　 B、3　　　　　　 C、4　　　　　　 D、5

7、4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180º后得到如图（2）所示，那么她所旋转的牌从左数起是　　　（　　　 ）

（A）第一张　  （B）第二张　　　　（C）第三张　　  　（D）第四张　

8、已知⊙O的半径为10cm，如果一条直线和圆心O的距离为10cm，那么这条直线和这个圆的位置关系为（　　　）

A、相离　　　　 B、相切　　　　　 C、相交　　　　　 D、相交或相离

9、反比例函数经过点P（），则它的图象在各自的象限内，随着的增大而　　　　  （　　　 ）

A、增大　　　　 B、无法判定　　　　　 C、不变　　　　  D、减小

10、一列列车自2004年全国铁路第5次大提速后，速度提高了26千米/时，现在该列车从甲站到乙站所用的时间比原来减少了1小时，已知甲、乙两站的路程是312千米，若设列车提速前的速度是x千米，则根据题意所列方程正确的是（　　　　）

A、　　　　 　　B、

C、　　 　　 D、

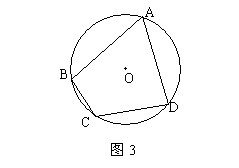
11、如图3，ABCD为圆内接四边形，若 ，则 等于（ ）

A、　　　 B、 　　　　 C、　　 　　D、

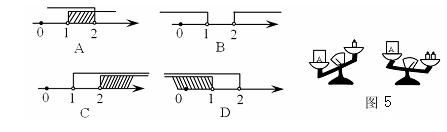12、如图5，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上

可表示为（　　　）

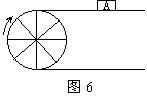13、如图6，当半径为30cm的转动轮转过120°角时，传送带上

的物体A平移的距离为（　　　）cm。

（A）20　 　（B）　　（C）300　　 （D）600

14、不解方程，判别方程的根的情况是　 (　　　).

（A）有两个相等的实数根　　　（B）有两个不相等的实数根　　　

（C）只有一个实数根　　　　　（D）没有实数根

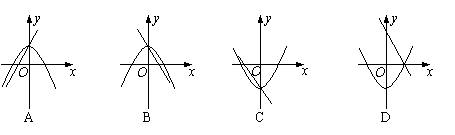15、在同一直角坐标系中，一次函数和二次函数的图象大致为（　　　 ）

16、下列调查方式合适的是（　　 ）

A、为了了解炮弹的杀伤力，采用普查的方式

B、为了了解全国中学生的睡眠状况，采用普查的方式

C、为了了解人们保护水资源的意识，采用抽样调查的方式

D、对载人航天器“神舟五号”零部件的检查，采用抽样调查的方式

17、某村的粮食总产量为a（a为常量）吨，设该村粮食的人均产量为y（吨），人口数为x，则y与x之间的函数图象应为图中的（　　　）

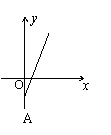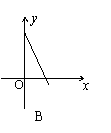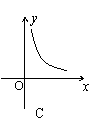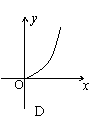二、填空题：（共10小题，每题4分，共40分）

1、相反数是　　　　，的平方根是　　　　　  。

2、的系数是　　　　。的余角的补角是　　　　　  。

3、 2003年10月15日中国“神舟”五号载人飞船成功发射，圆了中国人千年飞天的梦想，航天员杨利伟乘飞船在约21小时内环绕地球14圈，每圈长度约42179km。那么飞船环绕地球14圈的长度用科学记数法表示约　　　　 （结果保留三个有效数字）。

4、不等式组的解集是　　　　　　

5、正边形的一个内角等于 则=__________.

6、函数y =中，自变量x的取值范围是 　　　　 。

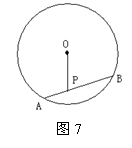
7、如图7，P是⊙O的弦上一点，AB = 10cm，AP = 4cm，OP = 5cm，则⊙O的半径为　　　　 cm。

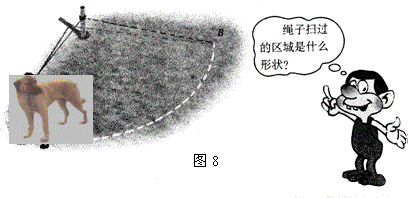
8、、如图8，一只狗拴在

一个木桩上，绳子长为8

米，当绳子被狗拉紧时，

狗运动后绳子“扫”过

130 ⁰的区域是　　　　 

形状。面积为　　　　米²（运动时狗视为点）。

9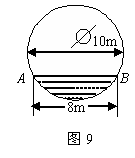、在直径为10m的圆柱形油槽内装入一些油后，截面如图所示，

如果油面宽AB=8m，那么油的最大深度是_____　　　　  _m。.

10、在一次中考数学研讨会上，参加会议的人，每两人都握过

一次手，有人统计共握了91次，那么到会的人数有　　　　 人。

三、解答题：（共4小题，每题5分，共20分）

1、计算：－2²+　()⁰+　2sin30^º

2、解不等式组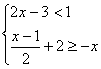，并把解集在数轴上表示出来。

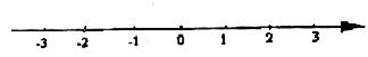
3、先化简代数式，然后请你自取一个你喜欢的的值代入求值。（所取的值要保证原代数式有意义哟）

4、解方程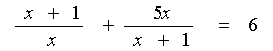

四、解答题：（共2个小题，每题6分，共12分）

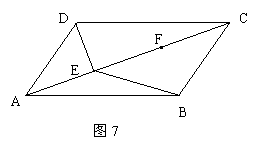
1、如图，在ABCD中，点E、F在对角线AC上，且AE＝CF．请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只需证明一组线段相等即可）．

⑴ 连结______________．⑵ 猜想：____________ ＝ ____________．

⑶ 证明：

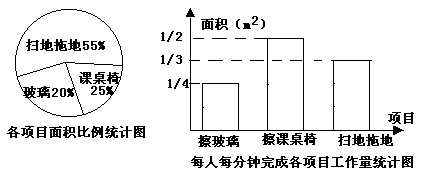2、某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80m²的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：

（1）从上述统计图中可知：

每人每分钟给擦课

桌椅　　　　　　 m²；

擦玻璃、擦课桌椅、扫地拖

地的面积分别是　　　　　 m²，　　　　　　  m²，　　　　　　  m²；

（2）如果x人每分钟擦玻璃的面积是ym²，那么y关于x的函数关系式是　　　　　　　 ；

（3）他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，该如何分配这两组的人数，才能最快地完成任务。

五、解答题：（共2个小题，每题6分，共12分）

1、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，

∠POC＝∠PCE。

（1）求证：PC是⊙O的切线；

（2）若OE：EA＝1：2，PA＝6，求⊙O的半径；

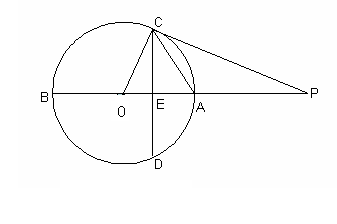（3）求sin∠PCA的值。

　

2、如图，由七个边长为1的正方形组成，过C点作直线交DE于A，交DF于B.

⑴若DA =，求DB的长；

⑵若DA、DB是方程的两根，求的值；

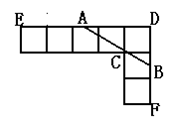⑶估计AB的长度的范围.

 

 

 

 

六、解答题：（共2个小题，第1小题7分，第2小题8分）

 1、 阅读下列材料，并解决后面的问题．

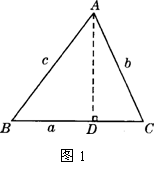　在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c．过A作AD⊥BC于D(如图)，则sinB =，sinC = ，即AD = csinB，AD = bsinC，于是csinB = bsinC，

即．

　同理有，．

　所以……………………………(*)

　即：在一个三角形中，各边和它所对角的正弦的比相等．

　(1)在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论(*)和有关定理就可以求出其余三个未知元素c、∠B、∠C，请你按照下列步骤填空，完成求解过程：第一步：由条件a、b、∠A　　　　　　　　　　　　∠B；

　　第二步：由条件　∠A、∠B． 　　　　　　　　　　 ∠C；

　　第三步：由条件．　　　　　　　　 　　　　　　　　　c．

(2)一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以28．4海里／时的速度按北偏东45°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西70°的方向上，求此时货轮距灯塔A的距离AB

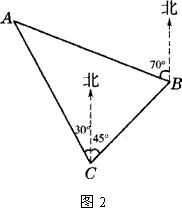(结果精确到0.1参考数据：sin40°= 0．6 43，sin65°= 0.906，　sin70°= 0.940，sin7 5°= 0.966)．

2、已知二次函数的图象与X轴交于A、B（）两点，其中

x₁，x₂是关于的方程的两个根，且这个二次函数的图象顶点P到轴的距离为9。

（1）求的值及A、B两点的坐标。

（2）写出这个二次函数的解析式。

（3）如果这个二次函数的图象与轴交于点C，试问：在轴上是否存在点D，使得△AOD与以B、O、C为顶点的三角形相似？若存在，求出所有符合条件的点D的坐标；若不存在，请说明理由。