初三数学试卷
一、选择题:![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、已知![]() ,则代数式
,则代数式![]() 的值是
的值是
A)0 B)2 C)4 D)6
2、已知![]() 且
且![]() 则
则![]() 的值为
的值为![]()
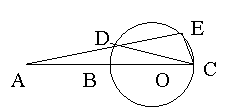 3、BC是圆O的直径,
3、BC是圆O的直径,![]() ,那么
,那么![]()
4、过点(1,3)作直线l,若l经过(a,0)和(0,b)两点,且a,b为正整数,则可作出的l的条数为
A)1条 B)2条 C)3条 D)多于3条
5、在梯形ABCD中,AD//BC,![]() E、M、F、N分别为AB、BC、CD、DA的中点,已知BC=7,MN=3,则EF=
E、M、F、N分别为AB、BC、CD、DA的中点,已知BC=7,MN=3,则EF=
![]() A)4
B)
A)4
B)![]() C)5
D)6
C)5
D)6
6、设[t]表示不大于t的最大整数,如[1]=1,[1.2]=1,则方程[3x+1]=6x的根共有
A)0个 B)1个 C)2个 D)3个
 7、正方形OPQR内接于
7、正方形OPQR内接于![]() 已知
已知![]() 的面积分别为
的面积分别为![]() 那么
那么
正方形OPQR的边长是
![]()
8、若函数![]() ,则当x取1,2,3,…,100个自然数时,函数值的和是
,则当x取1,2,3,…,100个自然数时,函数值的和是
A)270 B)195 C)194 D)97
9、在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,![]() 分别是垂足,则PE+PF=
分别是垂足,则PE+PF=
![]()
10、锐角![]() 三边两两不等,D是BC边上一点,且
三边两两不等,D是BC边上一点,且![]() , 则AD一定过
, 则AD一定过![]()
A)外心 B)重心 C)内心 D)垂心
11、一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为

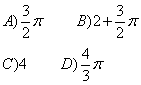
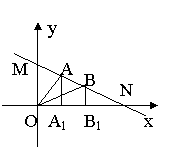 12、函数
12、函数![]() 的图象交y轴于M,交x轴于N,MN上两点A、B在x轴上射影分别为
的图象交y轴于M,交x轴于N,MN上两点A、B在x轴上射影分别为![]() ,若
,若![]() 则
则![]() 的面积
的面积![]() 与
与![]() 的面积
的面积![]() 的大小关系是
的大小关系是

二、填空题:![]()
13、若点![]() 和点
和点![]() 都在抛物线
都在抛物线![]() 上,则线段PQ的长是
上,则线段PQ的长是
14、在直角坐标系中,有点![]()
当四边形ABCD的周长最短时,直线CD的解析式是
15、以线段AB为直径作一个半圆,圆心为O,C是半圆周上的点,且![]() ,则
,则![]()
16、数学拓展课上,老师定义了一种运算“*”,对任意正整数n,满足以下运算性质:(1)2*2=1,(2)(2n+2)*2=3(2n*2),则2n*2用含n的代数式表示为
17、对于所有的正整数k,设直线![]() 与两坐标轴所围成的直角三角形的面积为
与两坐标轴所围成的直角三角形的面积为![]() ,则
,则![]()
18、有一张三角形纸片,内部有6个点,已知这6个点连同三角形纸片的三个顶点共9个点中无任何三点共线,则用剪刀将纸片剪开(以这9个点中的三个点为顶点),最多能剪成 个三角形纸片。
三、解答题:![]()
19、已知![]() 求
求![]() 的值。
的值。
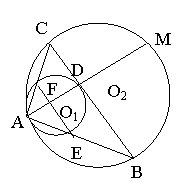
20、圆![]() 与圆
与圆![]() 内切于点A,
内切于点A,![]() 的弦BC切
的弦BC切![]() 于D,AD的延长线交
于D,AD的延长线交![]() 于M,连接AB,AC分别交
于M,连接AB,AC分别交![]() 于E、F两点,连接E、F
于E、F两点,连接E、F
1)
求证:![]()
2)
若![]() 的半径
的半径![]() BC是
BC是![]() 求AB和AC的长(AB>AC)
求AB和AC的长(AB>AC)
 |
21、淮安市某商场设有百货部、服装部和家电部三个经营部,共有190名售货员,计划全商场日营业额(指每日卖出商品所收到的总金额)为60万元,根据经验,各部商品每1万元营业额所需售货员人数如表1,每1万元营业额所得利润如表2。商场将计划日营业额分配给三个经营部,同时适当安排各部的营业员人数,若商场预计每日的总利润为c (万元)且满足![]() ,又已知商场分配给经营部的日营业额均为正整数万元,问这个商场怎样分配日营业额给三个部?各部分别安排多少名售货员?
,又已知商场分配给经营部的日营业额均为正整数万元,问这个商场怎样分配日营业额给三个部?各部分别安排多少名售货员?
表1 表2
各部每1万元营业额所需人数表 各部每1万元营业额所得利润表
| 部 门 | 人 数 |
| 百货部 | 5 |
| 服装部 | 4 |
| 家电部 | 2 |
| 部 门 | 利 润 |
| 百货部 | 0.3万元 |
| 服装部 | 0.5万元 |
| 家电部 | 0.2万元 |
22、是否存在周长为6,面积为整数的直角三角形?若不存在,请给出证明;若存在,请求出所有可能的直角三角形的内切圆半径?
23、现代社会对破译密码的难度要求越来越高。有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26个自然数。见表格
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出如下一个变换公式:

将明文转换成密文,如![]() ,即h变成q;
,即h变成q;
![]() ,即e变成c
,即e变成c
1) 按上述方法将明文good译成密文;
2)
若按上述方法将某明文译成的密文是shxc,请你找出它的明文。![]()
24、已知函数![]() ,我们把x=m时的函数值记作f(m),即
,我们把x=m时的函数值记作f(m),即![]() 。对任意x,都有
。对任意x,都有![]() 且
且![]() 。已知函数图象与x轴的交点分别为A、B,与y轴的交点为C,其顶点为M点。在直角坐标系中,O为坐标原点,以AB的中点P为圆心,AB为直径的圆P刚好过C点。
。已知函数图象与x轴的交点分别为A、B,与y轴的交点为C,其顶点为M点。在直角坐标系中,O为坐标原点,以AB的中点P为圆心,AB为直径的圆P刚好过C点。
1) 求此抛物线的解析式;
2) 设点D是抛物线与圆P的第四个交点,(除A,B,C三点以外),求直线MD的解析式;
3)
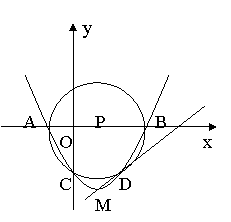 判断(2)中直线MD与圆P的位置关系,并说明理由。
判断(2)中直线MD与圆P的位置关系,并说明理由。


数学答案
一、选择题:![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | C | B | A | C | C | B | A | A | D | A |
二、填空题:![]()
13、![]() ;
14、
;
14、![]() ;
15、
;
15、![]()
16、3n-1; 17、![]() ;
18、13
;
18、13
三、解答题:![]()
19、解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
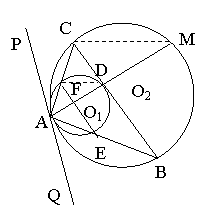 20、解:
20、解:
1)过A作两圆的公切线PQ,
![]()
![]() 所以EF//BC
所以EF//BC
连接DF、CM,∵BC切圆![]() O1于D,∴∠CDF=∠CAD
O1于D,∴∠CDF=∠CAD
又EF//BC,∴∠CDF=∠EFD,
而∠EFD=∠BAD,∠CAD=∠BAD,
又∠M=∠B,∴△ACM∽△ADB
∴AC:AD=AM:AB
即:![]()
2)∵BC是圆O2的直径,∴∠CAB=Rt∠,∴EF为圆O1的直径
∵EF=6,BC=16,EF//BC,∴![]()
∴AE:EB=3:5,设AE=3a,EB=5a,同理设AF=3b,FC=5b
在Rt△AEF中(3a)2+(3b)2=62,即a2+b2=4
设CD=x,BD=y,由切割线定理得x2=5b·8b=40b2,y2=5a·8a=40a2
∴x2+y2=40(a2+b2)=160,
又r2=8, ∴x+y=16
解得:x1=4,y1=12;x2=12,y2=4(舍)
∴![]() ,∴
,∴![]()
同理:![]()
所以![]()
21、解:设商场分配给百货、服装、家电营业额分别为x,y,z(万元),
x,y,z为整数,则
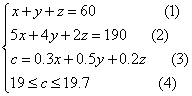
由(1)、(2)得: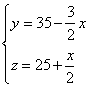
∴c=0.3x+0.5(35-1.5x)+0.2(25+0.5x)=22.5-0.35x
代入(4)得8≤x≤10
∵x,y,z为正整数,
∴x=8,y=23,z=29;或x=10,y=20,z=30
∴5x=40,4y=92,2z=58,或5x=50,4y=80,2z=60
答:分配给三个营业部的日营业额分别为8,23,29万元或10,20,30万元;三个部分别安排营业员40,92,58名或50,80,60名。
22、解:设斜边长为c,两直角边分别为a,b,则a+b+c=6
∴a+b=6-c (1)
两边平方得:a2+b2+2ab=36-12c+c2
∵a2+b2=c2,∴2ab=36-12c即ab=18-6c (2)
由(1)、(2)知:方程x2-(6-c)x+(18-6c)=0必有实根a,b
∴△=(6-c)2-4(18-6c)≥0,即c2+12c-36≥0
∴c≥![]() ≈2.4
≈2.4
又c<a+b=6-c, ∴c<3, ∴2.4≤c<3,∴7.2≤3c<9
而由(2)得3c=9-![]() 为整数,∴3c=8即
为整数,∴3c=8即![]()
把c值代入方程可得![]()
∴满足条件的三角形存在且唯一,![]()
23、![]()
![]()
![]()
![]()
3) 原公式的逆变换公式为
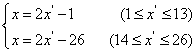
![]()
![]()
所以密文shxc的明文是love
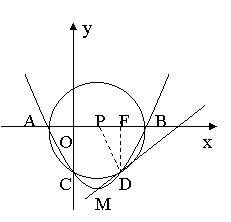 24、解:1)
24、解:1)![]()
![]()
![]()
∴所求抛物线解析式为![]()
2)![]()
∴顶点![]()
由图可知C、D两点关于直线![]() 对称
对称
∴可设D(m,-6),而D在抛物线上,
则![]()
解得:m=9或m=0(舍)
∴D(9,-6)
设过M、D两点 的直线解析式为y=kx+b
∴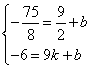 ,∴
,∴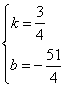
∴ 直线MD的解析式为![]()
3)作DF⊥AB于F,连接PD
直线MD与x轴的交点为E(17,0),而![]()
∴![]() DF=6,EF=8,
DF=6,EF=8,![]()
∴![]()
即![]() ∴
∴![]()
故直线MD与圆P相切