初中毕业班数学综合测试（一）
说明：本试卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷为选择题，满分为33分.第Ⅱ卷满分为117分，共150分.全卷共九大题，考试时间为120分钟，试题卷共6页，另有答题卷6页，共12页. 选择题按要求用铅笔将答题卡上对应题目的答案标号涂黑,填空题和解答题答案必须写在答题卷上;上交答题卡和答题卷.
第Ⅰ卷（选择题）
一、 选择题（本题共有11小题，每题3分，共33分）.
注意：每题只有一个符合题意的选项，不选、错选、 多选均不给分.
1. 据测算，我国每年因土地沙漠化造成的经济损失为547.5亿元，用科学记数法表示我国一年因土地沙漠化造成的经济损失为 （ * ）
（A）5.475×1010（元） （B）5.475×1011 （元）
（C）54.75×1010（元） （D）54.75×1011（元）
2. 下列等式中,成立的是 （ * ）
（A）(-2)0=0 （B）
（C）
（D）
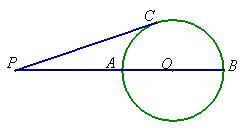
3. 如图，AB是⊙O的直径，点 P在 BA的延长线上，
PC是⊙O的切线 ，C为切点，PC＝
，PA＝2，
则⊙O的半径等于（ * ）
（A）1 （B） 2
（C）
（D）
（第3题）
4. 函数
自变量的取值范围是（ * ）
（A）x≥－2 （B）－2≤x＜1
（C）x＞1 （D）x≥－2且x≠1
5. 在Rt△ABC中，∠C＝90°，a：b＝3：4，运用计算器计算，∠A的度数是
（精确到1°） （ * ）
（A）30° （B）37° （C）38° （D）39°
6. 下列函数中，，当x＞0时，y随x 的增大而减小的是 （ * ）
（A）y= x （B）y=
（C）y=－ （D）y= x2
7. 若两个圆相外切，则两圆的圆心距（ * ）
（A）大于两圆半径的和 （B）等于两圆半径的和
（C）小于两圆半径的和 （D）与两圆半径的和的大小关系不确定
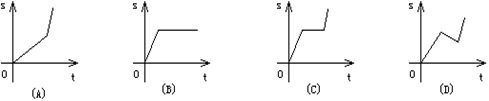
8. 某同学骑自行车上学，开始以正常速度匀速行驶。但行至中途因车出了毛病，只好停下修车，车修好后，因怕耽误上课他比修车前加快了骑车速度继续匀速行驶。下面是行驶路程S关于行驶时间t的函数图象（见图），那么符合这个同学行驶情况的图象大致是
（ * ）
9. 抛物线
(a≠0)，Q（2，－1）是该抛物线的顶点，则
的值等于 （ * ）
（A）-1 （B）-2 （C）2 （D）1
10. 为鼓励节约用电,某地对用户用电收费标准做如下规定:如果每月每户用电不超过100度,那么每度电价按1元收费;如果超过100度,那么超过的部分每度按2元收费.某户居民在一个月内用电180度,他这个月应缴纳电费（ * ）
（A）180元 （B）260元 （C）280元 （D）360元
11. ⊙O的半径为10，点P与O的距离为6，则过点P的弦AB的取值范围是 （ * ）
（A）6≤AB≤10 （B）3≤AB≤5
（C）12≤AB≤20 （D）16≤AB≤20
第Ⅱ卷（非选择题）
二. 填空题（本题共有6小题，每小题3分，共18分）
12. 已知∠α与∠β互余，且∠α=15°，则∠β的补角
为 度．
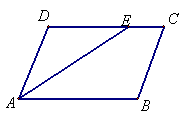
13. 如图，平行四边形ABCD中，AE平分∠DAB，
∠B=100°，则∠DAE等于 度.
（第13题）
14. 抛物线y＝x2＋x与直线y＝x的公共点的坐标是 ．
15. 已知⊙0的弦AB等于半径，C是⊙O上一点(不与点A,B重合)，则圆周角∠ACB的度数是 .
16. 某养鱼户去年在鱼塘中投放了一批鱼苗，现在为了解这批鱼的生长情况，从中捞取十五条鱼，测得其重量如下（单位：kg）:
1.2， 1.1， 0.9， 0.8，1.3， 1.2，1.3，1.0，1.0，1.2，1.5，1.3，1.7，0.9，1.0;
试计算这批鱼重量样本的方差是 ．(精确到0.0001)
17. 等边△ABC的各边与它的内切圆相切于
，
的各边与它的内切圆相切于
，……，以此类推.若△ABC的面积为1，则
的面积为
．
三. 作图题（8分），（说明：要求写出作法，只要求画出符合条件的一个圆和一个三角形.）
18. 已知：如图，A是直线l外的一点．
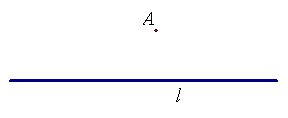求作：（1）一个⊙O，使它经过A点且与
直线l相切于B.
（2）一个直角△ABC使它内接于⊙O.
（第18题）
四. （本题共有2小题,每小题9分,共18分）
19. 解方程 
.
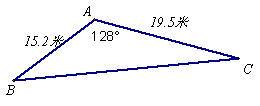
20. 我们学校在“美化校园”计划中将一块如图
所示的三角形
米，
米，
，空地上种植某种草皮以美化环境，
已知这种草皮每平方米92.5元，则购买这种草皮至少要多少元?（精确到1元）
（第20题）
五. （本题满分13分）
21. 写出一个形如关于x的一元二次方程
,使它的两个根中,一个根
大于1,另一个根
小于1；并求
的值。
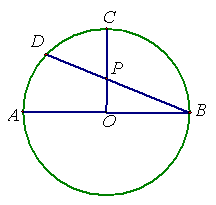
六. （本题满分13分）
22. 如图，已知AB是⊙O的直径，半径CO⊥AB于O，
P是CO上的一个动点，连结BP并延长交⊙O于点D，
如果⊙O 的半径为2，求BP·BD的值或其取值范围.
.
（第22题）
七. （本题满分15分）
23. 如图，一次函数的图象与x轴、y轴分别交于
A、B两点，与反比例函数的图象交于C、D两点．
如果A点坐标为（2，0），C、D分别在第一、三
象限，且
． 试求一次函数和反
比例函数的解析式．
（第23题）
八. （本题满分16分）
24. 已知在直角梯形ABCD中，∠A＝∠B＝90°,
BC= 2AD，ED⊥DC交AB于E，连结EC（AB＞AE）．
（1）△ADE与△EDC是否相似，若相似，证明你的结论；
若不相似，请说明理由；
（2）设
＝k，是否存在这样的k值，使得△ADE∽△BCE． （第24题）
若存在，证明你的结论并求出k的值；若不存在，说明理由．
九（本题满分16分）
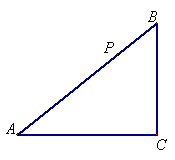
25. 如图，在△ABC中∠C =
.P为AB上一动点，
且点P不与点A和B重合，过点P作PE⊥AB交AC
边(或者CB边)于E点，点E不与点C重合，可将
△ABC分割成一个小三角形和一个四边形,若AB=5，
AC = 4；设AP的长为x，分割的四边形的周长为y，
求y与x之间的函数关系式,并求出x的取值范围． （第25题）
初中毕业班综合测试
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 总分 |
| 得分 |
|
|
|
|
|
|
|
|
|
|
数 学（一）答题卷
第Ⅱ卷（非选择题）
二. 填空题（本题共有6小题，每小题3分，共18分）
| 题号 | 12 | 13 | 14 | 15 | 16 | 17 |
| 答案 |
|
|
|
|
|
|
三. 作图题（8分），（说明：要求写出作法，只要求画出符合条件的一个圆一个三角形.）
18. 作法：
四. （本题共有2小题,每小题9分,共18分）
19.
20.
五. （本题满分13分）
21.
六. （本题满分13分）
22.
七. （本题满分15分）
23.
八. （本题满分16分）
24.
九（本题满分16分）
25.