初三第二学期数学期中测试试题
一、填空：（2’*25=50’）
1、抛物线
的对称轴是
，顶点坐标是 ，当
时，抛物线上的点都在轴的上方。
2、当
时，函数
是二次函数。
3、将函数向上平移
个单位，再向右平移1个单位，所得抛物线的解析式为
，此时顶点坐标为 ，对称轴为 。
4、抛物线
与
轴的交点坐标是
，与轴的交点坐标是
。
5、底边是边长为x的正方形，高是2的长方体，它的体积
，表面积为
。
6、已知抛物线
的顶点在x轴的上方，则m
。
7、二次函数
的图像经过四个象限，且定点在第三象限，则a，b，c及
的符号为a 0，b 0，c 0， 0。
8、在Rt△ABC中，∠ACB＝90°，AB＝8cm，BC的垂直平分线DE交AB于D，则CD=
cm．
9、在等腰梯形ABCD中，AB//CD，AC与中位线EG相交于F，DC＝8cm，AB=20cm，则EG=
cm，EF：FG=
。
10、在一个平面内，一个菱形绕他的中心至少旋转 °，才能与原菱形重合。
11、“两直线平行，内错角相等”的逆命题为 ，他是一个 命题。
12、用反证法证明“在一个三角形中，如果两条边不等，那么它们所对的角也不等”，则需假设
。
13、吴小刚在八年级第二学期的数学成绩分别为平时成绩85分，期中考试80分，期末成绩95分，如果按照平时、期中、期末的权重分别为15％、30％、55％，则吴小刚该学期的总评成绩为 分。
14、有一则药品广告声称“某某药品的疗效是75％以上。”你听了这则广告以后有何想法
。
二、选择题(3’*6=18)
1、 下列函数中，是二次函数的是：（ ）
①
②
③
④
⑤
⑥
⑦
⑧
A.3个 B.4个 C.5个 D.6个
2、下列函数中，y随x的增大而减小的是（ ）
A.
B.
C. 
D.
3、在同一坐标系内，函数
与
（
的大致图形是（
）
4、如图，在△ABC中，∠ACB＝90°，∠B＝30°，AD是角平分线，DE⊥AB于E，AD、CE交于G，则图中共有等腰三角形（ ）
A.1个 B.2个 C.3个 D.4个
5、如果顺次连接四边形各边中点所组成的四边形是菱形，那么原来的四
边形的对角线（ ）
A.互相平分 B.相等 C.互相垂直D.互相垂直平分
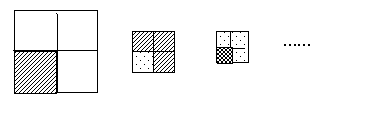
6、小王将一张正方形纸片撕成四张后，取其中一张载撕成四张，又取其四张中的一张在撕成四张……如此继续，在下面给出的四组数据中，哪一个是小王经过若干次撕纸后撕成的碎纸片数（ ）
A.2002 B.2003 C.2004 D.2006
三、计算题：(5’)
四、解答题：(57’)
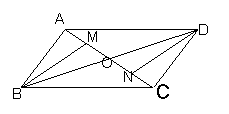
1. 如图，平行四边形ABCD的对角线AC与BD相交于O，M、N分别是OA、OC的中点。求证：BM=DN且BM//DN。(5’)
2. 王胜家所在的居委会通知居民可以根据自愿安装分时电表，但要缴纳成本及安装费100元．王胜的爸爸说安装费太贵了，王胜却认为使用分时电表更合算．你能利用下面给出的数据帮助王胜说服他的爸爸吗？(8’)
（1） 旧电表的收费标准：0.60元/度；
新电表的收费标准：0∶00～5∶00为0.30元/度，5∶00～24∶00为0.60元/度．
（2） 一般用电情况：0∶00～5∶00为5度/月，5∶00～24∶00为80度/月．1、7、8、12月（使用空调）用电情况：0∶00～5∶00为50度/月，5∶00～24∶00为200度/月．
3、 大妈参加了一种投资保障型家庭财产保险，她一次投资金2000元，投保3年，每年需教保险费12元（收益金中扣除），期满后，保险公司从收益金中扣除每年需交的保险费，连同保险投资金张大妈一共能领到2069元。试问：（1）张大妈投保3年期的收益率是多少？（收益金＝投资金×年收益率×保险年数）？（2）若张大妈把这2000元存入银行，存期三年，仅从经济角度考虑，请你为张大妈算一算，上述两种投资，那一种更合算？（利息＝本金×年利率×储存年数。三年期年利率是2.52％，利息税20％）？(8’)
4、 下面的统计图反映了某中国移动用户5月份手机的使用情况，该用户的通话对象分为三类：市内电话，本地中国移动用户，本地中国联通用户。
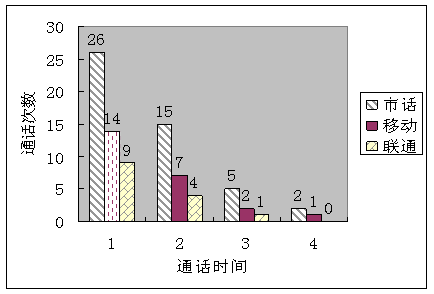
（1）该用户5月份通话总次数为 次。
（2）已知该用户手机的通话均按0.6元/分钟计算，求该用户5月份的话费（通话时间不满一分钟按一分钟计算。例如，某次实际通话费用为1分23秒，按通话时间2分钟计费，花费1.2元）；
（3） 当地中国移动公司推出了名为“越打越便宜”的优惠业务，优惠方式为：若与其他中国移动用户通话，第一分钟为0.4元，第二分钟为0.3元，第三分钟就降为每分钟0.2元，每月另收取基本费10元，其余通话计费方式不变，如果使用了该业务，则该用户5月份的话费会是多少？
5、 阅读并解答：
供应站应建在何处
[问题]如果一条流水线上依次排列的10台机床在工作，要设置一个零件供应站P，使这10台机床到供应站P的距离总和最小，这个零件供应站应该设在何处？
[分析]把问题退到最简单的情形
如图，如果流水线上只有2台机床时，很明显设在A1、A2之间的任何地方都行―――反正甲乙所走过的距离之和总是从A1到A2这一段路。
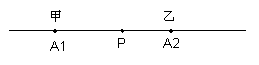
如图，如果在流水线上有3台机床时，不难推断，供应掌P设在中间一台机床A2处最合适。如果P放在A2处，甲、丙走过的距离和正好为A1到A3的距离，而如果放在别处，例如放在D处，那么甲、丙所走的距离和仍是A1到A3的距离，可是乙还得走从A3到D的这一段，这是多出来的。因此，P放在A2处为最佳选择。
类似分析可知，如果流水线上有4台机床，则P应在第2台和第3台之间任何地方，如果流水线上有5台机床，则P应设在 ；如果流水线上有10台机床，则零件供应站P应设在
。
阅读了以上材料，相信你一定能解答下面的问题：
某公司员工分别住在甲、乙、丙三个住宅区，甲区有10人，乙区有八人，丙区有13人，三个区在同一直线上，如图所示。该公司打算在此间设一个接送员工的汽车停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设置在（ ）
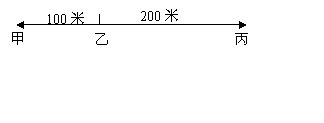A.甲区 B.乙区 C.丙区 D.乙丙两区之间
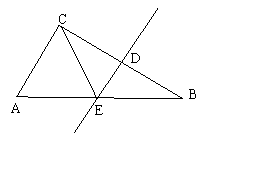
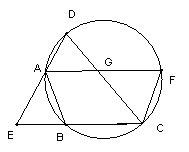
6、 四边形ABCD内接于圆，DA与CB的延长线交于点E，过点A作AF//BC交圆于点F，交CD于G。
（1） 求证：
;
（2） 若EB=FC，求证：△DEC为等腰三角形。
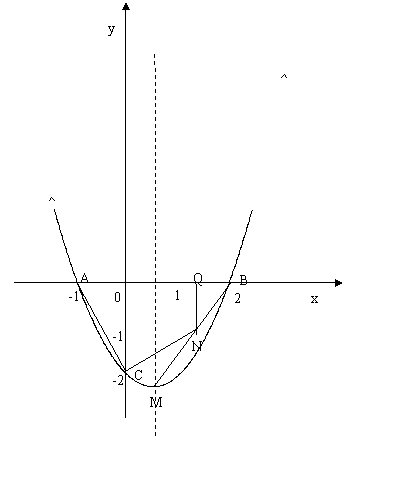
7、 知二次函数的图像如图所示。
（1） 求二次函数的解析式及顶点M的坐标；
（2） 若点N为线段BM上一点，过N作x轴的垂线，垂足为Q，当点N在线段BM上运动时（点N不与B、M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；
（3） 在对称轴的右侧的抛物线上是否存在点P使△PAC为直角三角形？若存在，求出P的坐标；若不存在，说明理由；
（4）
将△OAC补成矩形，使△OAC的顶点成为矩形一边上的两个顶点，另一个点落在矩形这一边的对边上，试直接写出矩形未知的顶点坐标（不需要计算过程）
