初三第一轮复习数学模拟试卷
（满分150分;考试时间：120分钟）
一、选择题：（本大题共7小题,每小题3分,共21分）（答案须填在答题卡）
每小题都有四个选项,其中有且只有一个选项是正确的.
1. 下列2个数互为相反数是
A．2与-2 B．2与0.5 C．3与1/3 D．4与±2
2. 下列事件中：确定事件是
A. 在同一年出生的360名学生中,至少有两人的生日是同一天.
B.从一副扑克牌中任意抽出一张牌,花色是红桃
C.任意选择电视的某一频道,正在播放动画片
D. 掷一枚六个面分别标有1～6的均匀骰子,骰子停止转动后偶数点或奇数点朝上
3.
在下列图形中,既是轴对称图形,又是中心对称图形的是
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
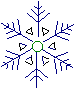A
B C D
4.满足不等式
的未知数
的整数解的个数是
A.2个 B.3个 C.4个 D.5个
5.计算
所得的结果是
A．1 B．2 C．3 D．4
6.小王利用计算机设计了一个计算程序,输入和输出的数据如下表：
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … |
|
|
|
|
| … |
那么,当输入数据是8时,输出的数据是
A.
B.
C.
D.
7.已知点
,
都在直线
上,则
与
的大小关系是
（A）
（B）
（C）
（D）不能比较
二、填空题：（本大题共10小题,每小题4分,共40分）（答案须填在答题卡）
8.按规律在横线填上一个数：1,－2,4,－8,_____;
9.电影院的8排10号用（8,10）表示,那么10排8号可用 表示;
10.因式分解
;
11.化简
;
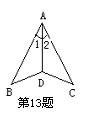
12.如图,已知扇形的圆心角为120°,扇形的面积为27πcm2,
则扇形的弧长= ;
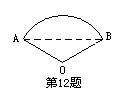
13. 如图,已知∠1=∠2,要使△ADB≌△ADC,还需添加一个
条件是 ;
14. 一个纸箱中有红、白2色的球共20粒,已知红球有8粒,则抽到白球的机会是 ;
15.在横线上填一个整数,使方程x2-x+( )=0在实数范围内有解,且解为无理数;
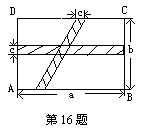
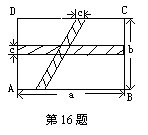
16. 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影
部分是平行四边形,依照图中标出的数据,则图中空白部分的
面积是 （用含a,b,c的代数式表示）;
17.某市为了鼓励居民节约用水,对自来水用户按如下标准收费：若每月每户用水不超过12吨,则按每吨x元收费;若超过12吨,则超过部分按每吨2x元收费.如果某户居民十月份交纳水费20x元,则该居民这个月实际用水__ _________吨.
三、解答题（共89分）
18.（本题满分8分）
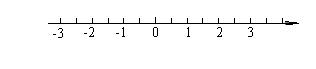解不等式组 
并把解集在数轴上表示出来.
19. （本题满分8分）
先化简
,再将x取一个适当的数,求出代数式的值.
20. （本题满分10分）
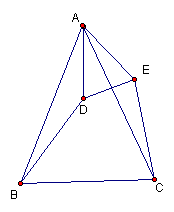
如图,△ABC和△ADE都是顶角为44°的等腰三角形,请在不添加辅助线的情况下找出图中的一对全等三角形,并给予证明.
21. （本题满分12分）
我国春节、“五一”、“十一”三个长假的假日经济的发展始终保持良好势头,假日经济的成长除了不断创新外,还有两条基本规律需要遵守,即提高服务、规范价格.下表是对长假期间价格与服务的感觉的民意调查
| 上升 | 基本没变 | 下降 | |
| 价格水平 | 64.5% | 26% | 9.5% |
| 服务水平 | 12.5% | 44% | 43.5% |
（1）调查显示,64.5%的消费者感觉长假期间价格水平 , %感觉基本没变化,感觉价格水平上涨的比感觉价格水平下降的多了 个百分点;
（2）对于长假期间的服务水平, %的消费者感觉有下降,感觉服务水平提升的比感觉服务水平降低的少了 个百分点;
（3）由以上分析,你认为妨碍假日经济更快成长的主要原因是
（4）针对长假期间严重的扎堆现象（如找不到好住处、遭遇恶意服务、买不到车船机票、景点商场站台拥挤无秩序等）,有人建议开放法定节日外的带薪长假,某报社计划进行一次民意调查,以了解市民对这一提议的赞同程度.请你代报社确定调查对象,并设计开展调查时要提问的问题.
22. （本题满分7分）
我市规定学校半径200米范围内不得开设网吧,老王找到一个店面C,从校门口A向前120米到路口B,再向右转走140米到达店面C.如果老王在店面C处开设网吧,是否会被取缔？请从数学的角度说明理由.
23. （本题满分10分）
（1）为制作光盘的简易包装袋,需测量光盘的直径,现有一副三角板（边长超过光盘的直径）、刻度尺、笔、科测验纸,请利用提供的材料设计一个测量光盘直径的方案（可附图说明）;
（2）小明同学只有一把刻度尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上（直尺与光盘、光盘与三角板均仅有一个接触点）,并量出AB=3.5cm,他用这个方法测出了光盘的直径.请你帮他说明理由.
24. （本题满分10分）
已知一次函数：
①
、 ② 
、 ③ 
、
④ 
、⑤ 
、 ⑥
（1） 如果（-1,-1）在函数的图象上,求
;
（2） 将以上6个函数分类（每类至少2个）,并说明分类的依据;
（3） 求直线与直线的交角的度数.
25. （本题满分12分）
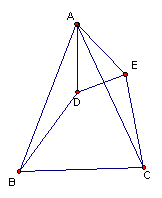
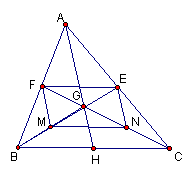已知：如图BE、CF、AH是ΔABC的中线,BE、CF、AH相交于G,
M、N分别是GB、GC的中点
（1）求证：四边形EFMN是平行四边形;
（2）①当
的值为 时,四边形EFMN是矩形;
②当
的值为 时,四边形EFMN是菱形;
（3）从第（2）小题的2个命题中,选择一题进行证明.完成第①题得4分,完成第②题得6分,多做不给分,请勿浪费时间.
26. （本题满分12分）
已知：
| x(h) | 0 | 3 | 6 | 9 | 12 |
| y(m) | 1.3 | 6.7 | 8.5 | 6.7 | 1.3 |
（1）请你以上表中的各对数据（x,y）作为点的坐标,在所给的坐标系中画出y关于x的函数图象（0≤x≤12）;
（2）选用一个函数来近似描述y与 x的函数关系,求出函数解析式;
（3）如果上表表示某港口某日从0时至12时的时间x(h)与水深y(m)的关系,已知一条货船的吃水深度（船底与水面的距离）为3.8米,安全条例规定至少要有1.5米的安全间隙（船底与洋底的距离）,在该日该船何时能进入港口？在港口能呆多久？
初三第一轮复习数学模拟试卷答案
一、选择题：每小题3分,共21分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 选项 | A | D | C | C | B | C | A |
二、填空题：每小题4分,共40分
8. 16； 9.（10，8）；
10.
11． 
；
12． 6πcm ； 13.AB=AC或∠B=∠C
14. 60%；
15.-1、-3、-4、-5、…….
16.ab-ac-bc+c2 17. 16吨.
三、解答题（共89分）
18.（本题满分8分）
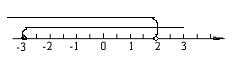
解(1) x≥-3……………………………………3分
解(2) x＜2……………………………………5分
结论：-3≤x＜2………………………………6分
……………………………………8分
19. （8分）=
…………………………………2分
=
…………………………………4分
=
…………………………………6分
x除-1外，其他均可代入
…………………………………8分
20. （本题满分10分）
解：△ABD和△ACE全等……………………2分
∵△ABC和△ADE都是顶角为44°的等腰三角形
∴AB=AC …………………………………3分
AD=AE …………………………………4分
∠BAC=∠DAE …………………………………6分
∴∠BAD=∠CAE…………………………………8分
∴△ABC≌△ADE…………………………………10分
21. （本题满分12分）
（1）价格水平上升，64.5%感觉基本没变化，多了55个百分点
（2）43.5%的消费者感觉服务水平有下降，少了31个百分点
（3）主要原因是价格水平上升、服务水平下降……………………………7分
（4）调查对象：（考虑年龄、工作性质、收入）……………………………9分
提出问题：是否同意开放法定节日外的带薪长假，等等……………………………12分
22. （本题满分7分）
会被取缔 …………………………1分
解1：AB=120，BC=140，∠ABC=90°
AC2=34000 …………………………4分
AC2小于40000
∴C点在学校半径200米范围内，会被取缔…………………………7分
解2：假设直线BC上有一点D，AD=200，…………………………2分
AB=120，AD=200，∠ABD=90°
BD=160，…………………………4分
BC小于160，C在线段BD上，
∴C点在学校半径200米范围内，会被取缔…………………………7分
23. （本题满分10分）
（1） 解1：利用90度的圆周角所对的弦是直径…………………………3分
解2：用笔在科测纸描出光盘的轮廓，对折，折痕为直径所在的直线…………3分
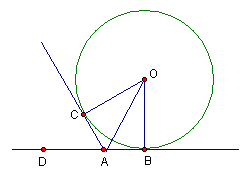（2）∵直尺与光盘、光盘与三角板均仅有一个接触点，∴AC切⊙O于C，AB切⊙O于B，且∠CAD=60°，………4分
∴∠OAB=∠OAC=
∠BAC=60°…………6分
∴∠OBA=90°…………………………7分
∵AB=3.5cm,tan∠OAB=
∴OB=ABtan60°=3.5………………………9分
∴直径为7cm…………………………10分
(其他解相应给分)
24. （本题满分10分）
（1） m=2 ……………………………………………2分
（2）
2类：①③④ 都过（0，0）
②⑤⑥ 都过（0，2） 3分，分类正确2分，理由1分
或3类：①②、③⑤、④⑥ 两两平行
………………………………………………5分
（3）设直线交y轴于A（0，2），交x轴于B（0，2）
直线交y轴于A（0，2），交x轴于C（0，-4）…………………8分
利用勾股定理，AB2=5，AC2=20，BC2=25 …………………9分
因为AB2+ AC2= BC2
所以两直线的交角成90度 …………………10分
25. （本题满分12分）
（1）证明：∵E、F分别为AC、AB的中点
∴EF平行且等于BC …………………1分
同理MN平行且等于BD，…………………2分
∴EF平行且等于MN …………………3分
∴四边形EFMN是平行四边形…………………4分
（2）1；
…………………6分
（3）解①：接（1）四边形EFMN是平行四边形
又AB=AC，H为BC中点，∴AH⊥BC…………………8分
得∠MFE为直角，…………………9分
∴四边形EFMN是矩形 …………………10分
解②：接（1）四边形EFMN是平行四边形
连结HN，证得HN∥BG，………………7分
EN∥AH………………8分
∴EN=GH…………………9分
又EN=0.5AG，∴EN=1.5AH…………………10分
MN=0.5BC …………………11分
当=时，MN=EN…………………12分
∴四边形EFMN是菱形
26. （本题满分12分）
（1）描点、连线…………………………………………3分
（2）
设解析式为
…………………………4分
解得a=-0.2…………………………6分
∴
………………………7分
（3）依题意，水深应超过5.3米………………………8分
当y=5.3时，求出x为2或10………………………10分
∴在该日该船2时能进入港口，呆在港口不能超过8小时。………………………12分