初三数学二模模拟试卷
2003.5.31
第一部分（满分100分）
一、填空题（每空2分，共26分）
1.的平方根是 ；设a*b＝2a＋b，则（m＋1）*（m－1）＝ ；
2. 点A（－3，2）关于y轴的对称点是 ；
函数y＝中，自变量x的取值范围是 ；
3. 若一组数据6，7，5，6，x，1的平均数是5，则这组数
据的众数是 ，方差
是 （结果保留一位小数）。
4. 如图，已知：AB为直径，∠ACD＝60°，
∠ADC＝70°，则∠APC＝ ；
5. 如图，一个圆环的面积为9π，大圆的弦AB切小
圆于C，则弦AB的长为 ；
6. 已知⊙O1的圆心坐标为（7，0），半径为1，⊙O2的圆心坐标
为（x，0），半径为2，若⊙O1与⊙O2相切，则⊙O2圆心坐标为 ；
7. 用一个半径为6cm的半圆围成一个圆锥，则该圆锥的锥角是 °，侧面积是
；
二、选择题（每小题3分，共18分）
8.若y＝,x＞0时，y随x的增大而减小，则y＝kx＋k的图象不经过（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.下列说法正确的是（ ）
A.2－3等于－8 B.零的相反数是它本身 C.是分数 D.实数的零次冥是1
10.若a－b＜0，则下列各式一定成立的是（ ）
A.a＞b B.ab＞0 C.＜0 D.－a＞－b
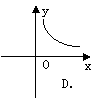
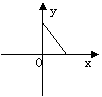
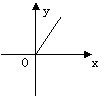
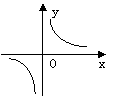11.某村的粮食总产量为a吨，该村粮食的人均产量为y，人口为x，则y与x的函数关系图象为（ ）
|
|
|
12.在①正多边形一定为轴对称图形，②等弧对等弦，③相等的圆心角所对的弧相等，④两圆最多有4条公切线，且它们都相等中，正确的命题有（ ）
A.1个 B.2个 C.3个 D.4个
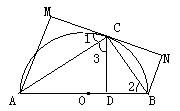
13.如图，AB是半圆O的直径，直线MN切半圆于C，CD⊥AB，
AM⊥MN，NB⊥MN，则下列结论中错误的是（ ）
A.∠1＝∠2＝∠3 B.AM·CN＝CM·BN
C.CM＝CD＝CN D.△ACM∽△ABC∽△CBN
三、解答题（其中14－18题每题6分，19－20题每题8分，计46分）
14.（＋1）0－｜sin60°－1｜－（）－1＋（－1）3
15.已知1≤x＜2，且5x－2y＝6，求y的整数解。
16.我市向西部某县赠送一批计算机，首批280台准备启运，经与某物运公司联系，得知用甲种汽车若干辆刚好装完；用乙种汽车不仅可少用四辆，而且有一辆车差20台计算机才装满，如果乙种车比甲种车每辆多装10台，求甲、乙两种汽车每辆各装计算机多少台？
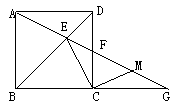17.已知：点E是正方形ABCD对角线BD上的一点，AE的延长线分别与CD、BC的延长线交于F与G，M为FG的中点。
|
18.如图，在菱形ABCD中，AE⊥BC于E点，EC＝1，sinB＝，求四边形AECD的周长。
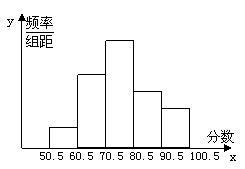19.某班同学参加法律知识竞赛，将竞赛所得成绩（得分取整数）进行整理后分成五组，并绘成频率分布直方图，五组频率之比为1:4:6:3:2，第三小组的频数为18，解答下列问题。
⑴该班共有多少名学生？
⑵60.5～70.5这一分数段的频数、频率分别为多少？
⑶这次竞赛成绩的中位数和众数能否确定在哪一组？
20.一居民小区搞绿化，要在一块矩形空地上建花坛，现征集设计方案，要求设计的花坛图象由圆和正方形组成（圆与正方形的个数不限），并使整个矩形场地成轴对称图形，请在所给矩形中画出你的设计方案。
 |
四、（本题满分10分）
21.已知：k为自然数，设α、β是x的方程kx2－2（k－3）x＋（k－3）＝0的两个不相等的实根，且一次函数y＝（k－2）x＋m与反比例函数y＝的图象都经过点（α＋1，β＋1），
且两图象相交于A、B两点，O为原点。
⑴求k的值； ⑵求一次函数和反比例函数的解析式； ⑶求△ABO的面积。
第二部分（满分50分）
五、选择题（每题3分，共15分）
22.若x2＋2x－2a中，有因式（x＋4），则a的值（ ）
A.8
B.－8
C.4 D.－4
23.设“■”、“▲”、“●”表示三个不同的物体，用天平
比较它们质量的大小，两次情况如图所示，那么这三个物
体按质量从大到小的顺序排列应为（ ）
A.■●▲ B.■▲● C.▲●■ D.▲■●
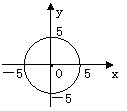
24.如图，P（x，y）是以坐标原点为圆心，5为半径的圆
周上的点，若x、y都是整数，则这样的点共有（ ）
A.4个 B.8个 C.12个 D.16个
25.某商品进货单价为30元，按40元一个销售，能卖40个；若销售单价每涨1元，销售量减少一个，要获得最大利润，此商品的最佳销售价应定为每个（ ）
A.50元 B.55元 C.45元 D.60元
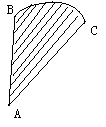
26.某工件形状如图所示，圆弧BC的度数为60°，AB＝6cm，
点B到点C的距离等于AB，∠BAC＝30°，则工件的面积等于（ ）
A.4π B.6π C.8π D.10π
六、（本题满分8分）
27.如果方程ax2＋bx＋c＝0（a≠0的两根和为S1，两根的平方和为S2，两根的立方和为S3，求证：aS3＋bS2＋cS1＝0
七、（本题满分8分）
28.某商场以每件30元的价格购进一种商品，试销中发现这种商品每天销售量m（件）与每天的销售价x元满足一次函数：m＝162－3x
⑴写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式。
⑵如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？
八、（本题满分8分）
29.如图，O是已知线段AB上一点，以线段OB为半径的⊙O交AB于C，以线段AO为直径的半圆交⊙O于D，过点B作AB的垂线与AD的延长线交于点E；
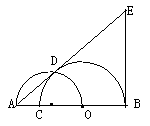⑴求证:AE切⊙O于D；
⑵若AC＝2，且AC、AD的长是关于x的方程x2－kx＋4＝0
的两根，求线段EB的长；
⑶点O是否在AB上存在一个位置使△DOC恰好等边三角形，若
存在，请求出点O位于线段AB何处；若不存在，请说明理由。
九、（本题满分11分）
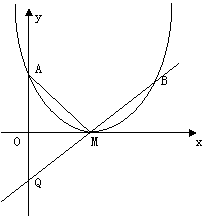
30.如图，抛物线y＝ax2＋bx＋c与x轴只有一个交点M，与y轴交于A点，且2ac＋b＝0，AM＝3，若直线y＝3ax＋k过M点与抛物线交于B点，与y轴交于Q点；
⑴分别求出二次函数和一次函数的解析式；
⑵以AB为直径作⊙O1，试判断该圆与两坐标轴的位置关系；
⑶过Q点作⊙O1的切线，切点为N，切线交过B点与y轴平行的直线于P，求QN·NP的值。
 |