九年级数学第一学期期末考试试卷
(本卷满分150分，考试时间：120分钟)
第一部分 选择题(共36分)
注意: 考生必须将所有答案填到答题纸上,答在试卷上无效。
一 、选择题（本大题共12小题，每小题3分，共36分 ）
1. 已知分式
的值为0，么x的取值是
A． 
B. 
.C
.
D. 以上均不对
2．稀土元素有独特的性能和广泛的应用，我国稀土资源的总储藏量约为1 050 000 000吨，是全世界稀土资源最丰富的国家．将1 050 000 000吨用科学记数法表示为
A、1．05×1010吨 B、 1．05×109吨
C、10．5×108吨 D、 0．105×1010吨
3．化简分式：
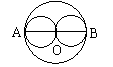
的正确结果是
A、
B、
C、
D、
4．一元二次方程
的一根为1,则
的值为
A、1或0 B、1 C、0 D、
5.抛物线
的顶点坐标是
A、
B、
C、
D、
6．下列调查的样本缺乏代表性的是 （ ）
A 为了解植物园一年中游客的人数，小名利用五一长假作了5天的进园人数调查
B 从养鸡场中随机抽取种鸡10只，来估计这批种鸡体重的平均值
C 为了解我市读者到市图书馆借阅图书的情况，从全年的借读人数中抽查了20天每天到图书馆借阅图书的人数
D 调查某电影院单排号的观众，以了解观众们对所看影片的评价情况
7．若一个圆锥的轴截面是等边三角形，其面积为
，则这个圆锥的侧面积是
（A）2π （B）
（C）4π
（D）以上都不对
8．如图，已知，MB=ND，∠MBA=∠NDC，下列哪个条件不能判定
△ABM≌△CDN的是
A. ∠M=∠N B. AB=CD
C. AM=CN D. AM∥CN
9．下列四个命题中错误的是
A. 两条对角线互相垂直且相等的四边形是正方形
B. 菱形的一条对角线平分一组对角
C. 顺次连结四边形的各边中点所得的四边形是平行四边形
D. 等腰梯形的两条对角线相等
10．将一张正方形的纸片按下图所示的方式三次折叠，
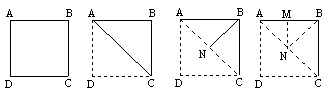折叠后再按图所示沿MN裁剪，则可得
A、多个等腰直角三角形 B、一个等腰直角三角形和一个正方形
C、四个相同的正方形
D、两个相同的正方形
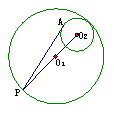
11． 如图，⊙
与⊙
内切，半径分别为3和1，的延长线交
于点P，作⊙的切线PA，切点为A，则PA的长为
A、
B、
C、
D、以上都不对
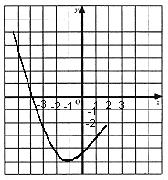
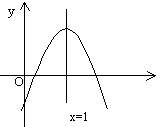12．二次函数
的图象如图所示，下列结论：
（1）
（3）
（4）
其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个
第二部分 非选择题（共114分）
二．填空题（本大题共8小题，每小题3分，共24分）
13．函数
的自变量
的取值范围是
；
14．已知抛物线
的顶点在轴上，则
=____________
15．两道单选题都含有A，B，C，D四个选择支，瞎猜这两道题，恰好全部猜对的概率是
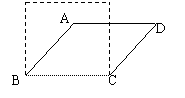
16、如图，若将四根木条钉成的矩形木框变形为平行四边形
ABCD的形状，使其面积为矩形面积的一半，则这个
平行四边形较小内角的值等于 。
17、一束光线从Y轴上点A（0，1）出发，经过X轴上的点C反射后经过点B（3，3）,则光线从A点到B点经过的路程长为
。
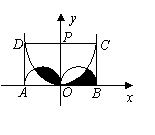
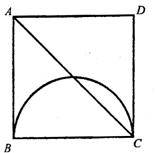
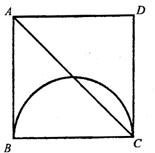
18．如图，矩形ABCD的长AB=4cm，宽AD=2cm.
O是AB的中点，OP⊥AB，两半圆的直径分别为AO
与OB.抛物线的顶点是O，关于OP对称且经过
C、D两点，则图中阴影部分的面积是 cm2.
19．已知没有画完的抛物线
的图象关于
对称，
有一个根是
，那么
这个方程的两根之和是 ；
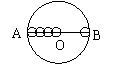
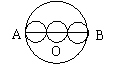
20．如图，AB是⊙O的直径，把线段AB分成几条相等的线段，以每条线段为直径分别画小圆，设AB＝，那么⊙O的周长为
,试计算：把AB分成两条相等的线段，每个小圆的周长
＝______；把AB分成三条相等的线段，每个小圆的周长
＝______；……；把AB分成
条相等的线段，每个小圆的周长
＝
．
（三）解答下列各题（共90分）
21.（本题8分）计算
22．（本题8分）先化简，再求值：
其中m＝
23.（本题8分）解方程
24．（本题10分）集市上有一个人在设摊“摸彩”，只见他手拿一个黑色的袋子，内装大小、形状、质量完全相同的白球20只，且每一个球上都写有号码（1－20号）和1只红球，规定：每次只摸一只球。摸前交1元钱且在1——20内写一个号码，摸到红球奖5元，摸到号码数与你写的号码相同奖10元。
(1) 你认为该游戏对“摸彩”者有利吗？说明你的理由。
(2) 若一个“摸彩”者多次摸奖后，他平均每次将获利或损失多少元
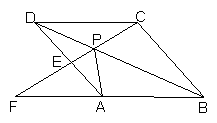25．（本题12分）如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F。
问：（1）图中⊿APD与哪个三角形全等？试证明
（2）⊿APE与哪个三角形相似？试证明
（3）猜想：线段AP、PE、PF之间存在什么关系？
说明理由。
26．（本题10分）图1是棱长为a的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…、第n层，第n层的小正方体的个数为s．解答下列问题：
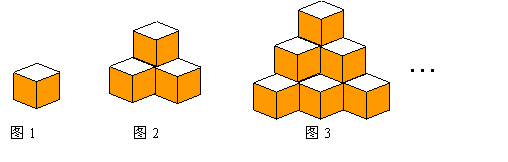
（1）按照要求填表：
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
（2）写出当n=10时，s = ．
（3）根据上表中的数据，把s作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点．
（4）请你猜一猜上述各点会在某一函数图象上吗？如果在某一函数图象上，求出该函数的解析式；如果不在某一函数图象上，说明理由．
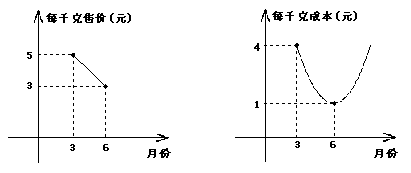
27.（本题10分）某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行销和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两方面的信息（如甲、乙两图）注：甲、乙两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本；甲图的图象是线段，乙图的图象是抛物线.请根据图象提供的信息说明，解决下列问题：⑴在3月份出售这种蔬菜，每千克的收益是多少？⑵哪个月出售这种蔬菜，每千克的收益最大？说明理由.（收益=售价-成本）
 |
28、(本题12分)⑴、如图：设正方形面积为S，它的两条对角线与一组对边所围成的两个三角形的面积分别为S1、S2，则三者之间存在的等量关系为_____ ____
_ __。
⑵、将⑴中的正方形改为矩形后，其余条件不变，则⑴中的等量关系是否成立？
____________________(填“是”或“不是”)。
⑶、将⑴中的正方形改为平行四边形后，依照⑴写出一个命题并判断真假(不要求证明)
_______________________________________________________________________________
⑷、设梯形ABCD的面积为S，AB∥DC，梯形的两条对角线与两底所围成的三角形面积分别为S1、S2，则之间有何等量关系，并证明你的结论。
______________________________________________________________________________⑸、根据⑴～⑷你可以归纳出结论：_________________________________________________
 | |||||||
 | |||||||
 |  | ||||||
29．（本题12分）已知，如图（1）正方形ABCD中，有一直径为BC的半圆，BC＝2cm。现有两点E，F，分别从点B，点A同时出发，点E沿线段BA以1cm/秒的速度向点A运动，点F沿折线A－D－C以2cm/秒的速度向点C运动，设点E离开点B的时间为t（秒）。
（１） 当t为何值时，线段EF与BC平行？
（２） 设1<t<2，当t为何值时，EF与半圆相切?
（３） 当1≤t<2时，设EF与AC相交于点P，问点E，F运动时，点P的位置是否发生变化？若发生变化，请说明理由；若不发生变化，请给予证明，并求AP∶PC的值。
(注：图（2）图（3）作解题备用)
九 年 级 数 学 答 题 纸 得分_______
一 、选择题（每小题3分，共36分 ）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二．填空题（每小题3分，共24分）
13._______________ 14.___________________ 15.______________
16._______________ 17.____________________ 18.________________
19._______________ 20.__________________
（三）解答下列各题（共90分）
21 (本题8分)
22(本题8分)
23(本题8分)
24(本题10分)
25(本题10分)