九年级中招模拟考数学卷
九年级数学试题
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 得分 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |||
注意事项：本试卷共8页，三大题，满分120分，考试时间100分钟。请用圆珠笔或钢笔直接答在试卷上。
| 得分 | 评卷人 |
|
|
一、选择题：（每题3分，共18分.）下列各题的四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内。
1. 下列多边形中，能够铺满地面的是（ ）
A、 正五边形 B、正六边形 C、 正七边形 D、正八边形
2. ．当你将一把扇形扇子逐渐打开时，容易发现打开部分的扇形面积随圆心角的变化而变化，那么下列函数中能正确描述这种变化的是( )
A．正比例函数 B．反比例函数 C．一次函数(b≠0) D．二次函数
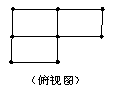
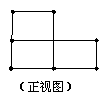3. 下列两个图是由几个相同的小长方体堆成的
物体视图，那么堆成这个物体的小长方体最多有（ ）个
A、5 B、6 C、4 D、3
4. 在一个地球仪的赤道上用铁丝打一个箍，现将铁丝箍半径增大1米，需增加ｍ米长的铁丝，假设地球的赤道上也有一个铁箍，同样半径增大1米，需增加ｎ米长的铁丝，则ｍ与ｎ的大小关系是（ ）
A、ｍ＞ｎ B、ｍ＜ｎ C、ｍ＝ｎ D、不能确定
5. “某市位处理污水，需要铺设一条长为4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时×××××。设原计划每天铺设管道x米，则可得方程
。”根据此情境，题中用“×××××”表示得缺失的条件，应补为（
）
A 每天比原计划多铺设10米，结果延期20天才完成任务
B 每天比原计划少铺设10米，结果延期20天才完成任务
C 每天比原计划多铺设10米，结果提前20天完成任务
D 每天比原计划少铺设10米，结果提前20天完成任务
6.
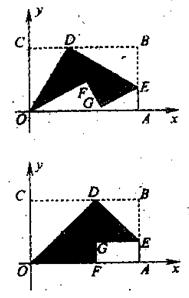
挪威数学家阿贝尔，年轻时就利用阶梯形，发现了一个重要的恒等式——阿贝尔公式：右图是一个简单的阶梯形，可用两种方法，每一种把图形分割成为两个矩形。利用它们之间的面积关系，可以得到：a1b1+a2b2=（
）
A a1(b1－b2)+(a1+a2)b1 B a2(b2－b1)+(a1+a2)b2
C a1(b1－b2)+(a1+a2)b2 D a2(b1－b2)+(a1+a2)b1
| 得分 | 评卷人 |
|
|
二、填空题（每小题3分，共27分）
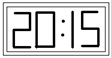7. 在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间应该是______.
8.在边长为3㎝、4㎝、5㎝的三角形白铁皮上剪下一个最大的圆，此圆的半径为___㎝.
9. 如下图是由边长为a和b的两个正方形组成，通过用不同的方法，计算下图中阴影部分的面积，可以验证的一个公式是 .
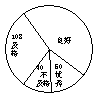
10. 九年级（1）班进行一次数学测验，成绩分为优秀、良好、及格、不及格四个等级．测验结果反映在扇形统计图上，如下图所示，则成绩良好的学生人数占全班人数的百分比是 %.
11. 如下图，正方形是由k个相同的矩形组成，上下各有2个水平放置的矩形，中间竖放若干个矩形，则k= .
12. 如下图，圆锥底面圆的直径为6cm，高为4cm，则它的全面积为 cm2 (结果保留π).
 | |||||
    | |||||
 | |||||
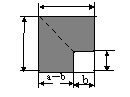第9题 第10题 第11题 第12题
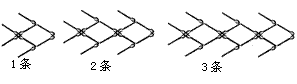
13. 如下图是小明用火柴搭的1条、2条、3条“金鱼”……，则搭n条“金鱼”需要火柴 根.
 |
……
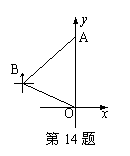
14. 如图，机器人从A点，沿着西南方向，行了个4单位，到达B点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为 （结果保留根号）．
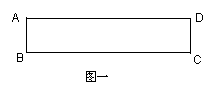
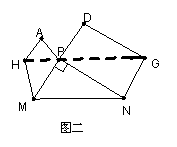
15. 把图一的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处（如图二）已知∠MPN=
，PM=3，PN=4，那么矩形纸片ABCD的面积为
。
三、解答题：（本大题有8小题，满分 75分）
| 得分 | 评卷人 |
|
|
16.（8分）
先化简代数式
，然后选取一个使原式有意义的a值代入求值.
| 得分 | 评卷人 |
|
|
17.(9分)
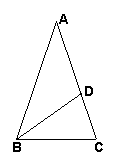如图，已知△ABC中，D是AC边上一点，∠A=36º，∠C=72º，∠ADB=108º。
求证：(1)AD=BD=BC；
(2)点D是线段AC的黄金分割点。
| 得分 | 评卷人 |
|
|
18.(9分)
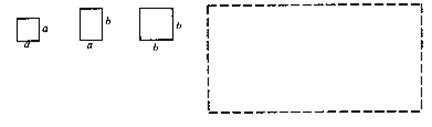
已知，如图，现有
、
的正方形纸片和
的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为
，并标出此矩形的长和宽。
| 得分 | 评卷人 |
|
|
19(9分)
某校初三年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面高
m，与篮圈中心的水平距离为7m，当球出手后水平距离为4m时到达最大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m。
（1）建立如图的平面直角坐标系，问此球能否准确投中？（4分）
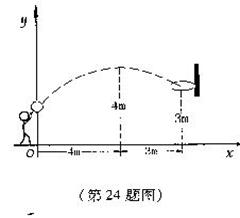（2）此时，若对方队员乙在甲前面1m处跳起盖帽拦截，已知乙的最大摸高为3.1m，那么他能否获得成功？ （5分）
| 得分 | 评卷人 |
|
|
20. (9分) 探索下列问题：
（1）在图1给出的四个正方形中，各画出一 条直线（依次是：水平方向的直线、竖直方
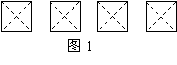向的直线、与水平方向成45°角的直线和
任意的直线），将每个正方形都分割成面积
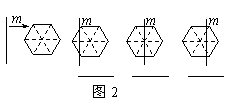相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，
在由左向右平移的过程中，将正六边形分成
左右两部分，其面积分别记为S1和S2.
①请你在图2中相应图形下方的横线上
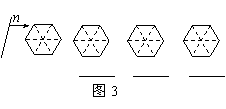分别填写S1与S2的数量关系式（用“<”，
“=”，“>”连接）；
②请你在图3中分别画出反映S1与S2
三种大小关系的直线n，并在相应图形下
方的横线上分别填写S1与S2的数量关系
式（用“<”，“=”，“>”连接）.
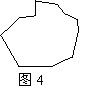（3）是否存在一条直线，将一个任意的平面图
形（如图4）分割成面积相等的两部
分，请简略说出理由.
| 得分 | 评卷人 |
|
|
21.（10分）
某校每学期都要对优秀的学生进行表扬，而每班采取民主投票的方式进行选举，然后把名单报到学校. 若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额，且各项均不能兼得. 现在学校有30个班级，平均每班50人.
（1）作为一名学生，你恰好能得到荣誉的机会有多大？
（2）作为一名学生，你恰好能当选三好生、模范生的机会有多大？
（3）在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中，哪些是解决上面两个问题所需要的？
（4）你可以用哪些方法来模拟实验？
| 得分 | 评卷人 |
|
|
22. （10分）
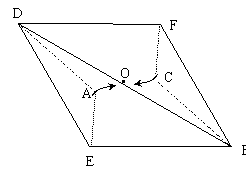
已知： ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．
⑴求证：四边形ABCD是矩形；
⑵在四边形ABCD中，求
的值．
| 得分 | 评卷人 |
|
|
23.（11分）如图一，平面直角坐标系中有一张矩形纸片OABC，O为坐标原点，A点坐标为(10，0)，C点坐标为(0，6)，D是BC边上的动点(与点B，C不重合)，现将△COD沿OD翻折，得到△FOD；再在AB边上选取适当的点E，将△BDE沿DE翻折，得到△GDE，并使直线DG、DF重合。
(1)如图二，若翻折后点F落在OA边上，求直线DE的函数关系式；
(2)设D(a，6)，E(10，b)，求b关于a的函数关系式，并求b的最小值；
(3)一般地，请你猜想直线DE与抛物线
的公共点的个数，在图二的情形中通过计算验证你的猜想；如果直线DE与抛物线始终有公共点，请在图一中作出这样的公共点。
