中考数学模拟试题（9）

中考数学模拟试题（9）

（时间120分钟　 满分150分）

一：选择题（每小题3分，共36分）

1．－的倒数是　　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

　（A）　　3　　　 （B）　　－3　　（C）　　　 （D）　－

2．下列运算正确的是　　　　　　　　 　　　　　　　　　　　　　　（　　）

　 （A） 3^-2= -9　　 （B） a²·a³=a⁵　 （C）a⁵+a⁵=2a¹⁰  （D）

3．下列图形中，对称轴最多的是　　　　　　　　　　　　　　　　　  （　　 ）

　　（A）　圆　　　 （B）　正方形　（C）　等腰三角形　（D）线段

4．在△ABC中∠C=90⁰，若∠B=2∠A则cotB等于　　　　　 　　　　 （　　 ）

　 （A） 　　　 （B） 　　（C）　　　　　　 （D）

5．关于x的一元二次方程(a-1)x²+x+a²-1=0的一个根为0，则a的值为　　（　　 ）

（A）　 1　　　 （B） －1　　　　（C） 1或－1　　　　 （D）

6．⊙0₁与⊙0₂内切，若⊙0₁的半径为2㎝，0₁0₂=1㎝　 则⊙0₂的半径为　（　  ）

（A）　 1㎝　　　 （B） 3㎝　　　　（C） 1㎝或3㎝　　　 （D）1.5㎝

7．相异两点A（3，5）B（x,y），若AB∥x轴，则下列结论正确的是　　 （ 　 ）

（A）x=3　　（B）y=3　　 （C） x=5　　　　 （D）y=5

8．正比例函数y=kx与反比例函数y=的图象相交于A，C两点，已知A点的坐标为（1，3），则点C的坐标为　　　　　　　　　　　　　　　　　　　　　  （　　）

　 （A）（1，-3）　　 （B） （-1，3）　　　（C） （-1，-3）　　（D）（-3，-1）

9．如果圆锥的底面半径为3㎝，母线长为4㎝，那么它的侧面积为　　　（　　）

（A） 24 ㎝²　　 （B） 12㎝²　　　（C）6 ㎝²　　　　（D）12 ㎝²

10．小王利用计算机设计了一个计算机程序，输入与输出数据如下表：

输入	…	1	2	3	4	5	…
输出	…		－		－		…

　 当输入值为8时，输出数据为　　　 　　　　　　　　　　　　　　（　　　）

　（A）　 　　 （B）　 －　　 （C）　　　　 （D）－

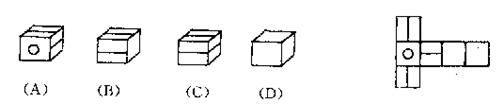
11右图代表未折叠正方体的展开图，将其折叠起来，变成正方体后，图形是　　　　　　　　　　　　　　　  是（　　）　　　　　　  　　　　　　　　　

　　

　　12．如图，点A、D、G、M在半圆O上，四边形ABOC，DEOF，HMNO均为矩形。设BC=a，EF=b，NH=c，则下列各式中正确的是　　　　　　　　　  （　 ）

　 （A） a>b>c　 （B） a=b=c　 （C）　c>a>b　 （D）b>c>a

二：填空题（每题4分，共32分）

13．在函数y=中自变量x的取值范围是____________

14．分解因式 ：x³－4x=___________________.

15．不等式组的解集为x≤－1，则k的值是______________.

16．若x=2^m, y=3+4^m，用含x的代数式表示y，则y=___________________.

17．某中学为了解全校的耗电情况，抽查了10天中全校每天的耗电量数据如下（单位：度）

度数	90	93	102	113	114	120
天数	1	1	2	3	1	2

则计算该校每天的平均用电量，并估计该校五月分的耗电量为_____________度

18．如图，点P为⊙0外一点，连OP交⊙0于点B，过点P作⊙0的切线PC，

切点为C，若PB=2，PC=4，则⊙0的半径为________

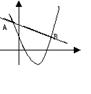19．如图已知二次函数y₁=ax²+bx+c(a≠0)与一次函数y₂=kx+m(k≠0)的图象

交于点A(－2，y_A),　　B（8，y_B）

则能使y₁>y₂成立的取值范围为_______________

20．我们学习过反比例函数。例如，当矩形面积s一定时，

长a是宽b的反比例函数，其函数关系式可以写为a=（s为常数，s≠0）。

　  请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式。

实例：_________________________________________________________________________________________________________________________________________________

函数关系式：__________________________________

三：解答题（82分）21．计算：（－）²+ － －（1－sin45⁰）⁰+　　 

 

22．有一块三角形的地，现要平均分四农户种植（即四等分三角形面积），请你在图上作出分法。（不写作法，保留作图痕迹）

23．“学校校办厂需制作一块广告牌，请师徒两名工人，已知师傅单独做需4天，徒弟单独做需6天，现由徒弟先做一天，再由两人合作完成，

（1）　　　　 前后共用几天完成了任务？

（2）　　　　 如果完工后共得报酬450元，现按各人完成任务的工作量计算报酬，该如何分配？

24．　若方程(2m-1)x²-2x+1=0有两个不相等实数根。

（1）求m范围；　　  （2）如果+=13, 求-值。

 

25、阅读下面题目的分析过程，再回答问题。

（3）若12分钟后只放热水，不进冷水，求y的表达式，并在图中把相应的图象补充完整．

设x,y为正实数，且x+y=4，求的最小值。

分析：（1）如图甲，作长为4的线段AB，过A、B两点在AB的同侧作AB的垂线AC、BD，使AC=1，BD=2.

（2）设P为AB上一个动点，PA=x，PB=y，由AB=4得x+y=4.连结PC、PD则PC=，PD=

（3）只要在AB上找到使PC+PD为最小的P点的位置，就可以计算出的最小值.

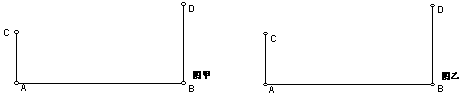
问题：（1）以上分析过程，体现的数学思想是_______________

　　 （2）在图乙中作出符合上述第三步的P点，并写出作法.

①____________________________________________

②____________________________________________

（3）当x+y=4时，求的最小值.

（4）用类似的方法，求出：当x+y=12时，的最小值.

是_________________

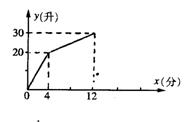26．海棠牌”电热水器，每单位时间内进出水的水量都是一定的，设从某一时刻开始4分钟内只进冷水，不出热水，在随后的8分钟内既进冷水又出热水，如果时间（分）与水量（升）之间的函数关系如图所示．

　 （1）每分钟进水多少？

　 （2）当时，与y有何关系？

27.我市某地一家农工商公司收获的一种蔬菜，共140吨，若在市场上直接销售，每吨利润为1000元，经粗加工后销售，每吨利润可达4500元，经细加工后销售，每吨利润可达6500元。

该公司加工厂的能力是：如果对蔬菜进行粗加工，每天可加工16吨；如果进行细加工，每天可加工6吨，但两种加工方式不能同时进行，受季节等条件限制，公司必须在15天内（含15天）将这批蔬菜全部销售或加工完毕。为此，公司研制了两种方案：

 方案一。尽可能多的对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接销售。

 方案二。将一部分蔬菜进行精加工，其余蔬菜进行粗加工。

（1）求出方案一所获利润W₁。

（2）求出方案二所获利润W₂（元）与精加工蔬菜数X（吨）之间的函数关系式。

（3）你认为应如何安排加工（或直接销售）使公司获利最多？最大利润是多少

28.一个圆形街心花园，有三个出口A、B、C，每个出口之间有一条长60米的道路，组成正三角形ABC，在中心点O处有一个亭子。为使亭子与原来的路相通，需修建三条小路OD、OE、OF，使另一出口D、E、F分别落在三角形ABC的三边上，且这三条路把三角形ABC分成三个全等的多边形，以备种植不同品种的花草。

（1）请你按以上要求设计两种不同的方案分别画在图1、图2上，并附简单说明；

（2）要使三条小路把三角形ABC分成三个全等的等腰梯形，应怎样设计？请把方案画在图3上，并求出此时三条小路的长度和；

（3）请你研究一种一般的方法，使得不论D在何处，都能准确的找出另外两个出口E、F的位置，请写出这个方法（图4供你探究用）

（4）你在图4中探究出的一般方法是否适用于正五边形？请结合图形进行说明。这种方法能推广到正n边形吗？