《函数及其图象》复习测练题
班级：________ 学号：________ 姓名：________ 成绩：________
一．选择题：(每小题3分，共18分)
1.已知：点A(0，1)、B(2，0)、C（0，0）、D(－1,0)、E(－3，0)，则在y轴上的点有（ ）
A．1个 B．2个 C．3个 D．4个
2. 在下列函数中，属正比例函数是（ ）
A．
B.
C.
D.
3. 经过点P(－1，2)的双曲线的函数关系式是（ ）
A. y =
B.
y =-2x C. y =－
D. y =－
4.如果k＜0，那么下列说法中正确的是（ ）
A.函数y = kx中，y随x的增大而增大
B.函数y =
的图象的两个分支分别位于第一、三象限
C.抛物线y = (x + k)2的对称轴是直线x = k
D.直线y = kx+k经过第二、三、四象限
5.抛物线
与y轴的交点坐标是（ ）
A.(－1，0) B.(0，-1) C.(0，1) D. (1，0)
6.函数y=kx+k与y=在同一坐标系是的大致图象是（
）
 |
二．填空题：(每小题4分，共32分)
1. 点M(4,-3)到x轴的距离为_______，它关于y轴的对称点的坐标为_______。
2. 函数
中自变量x的取值范围是_______。
3. 若每个同学都要购买4本练习本，且练习本的单价是0.2元，则总金额y(元)与学生个数x(个)的函数关系式是____________.
4. 一次函数y=-2x-3的图象不经过第_______象限。
5. 已知一次函数y=mx+(m+4)，它的图象经过点(1，2)，则其解析式是_____ __。
6. 若抛物线y=2x2－ax+m的对称轴是y轴，则a的值等于_______。
7.
如果函数
是一次函数，那么m的值等于_______。
8. 某种火箭烟花的飞行高度h（米）与发射后飞行的时间t（秒）之间的函数关系式是h＝－10 t2＋40 t，那么这种火箭烟花在发射______秒后又掉回到地面。
三．解答题(共32分)
1. 已知y+2与x成正比例，且x=8时，y=4，求当x=-2时，y的值。(5分)
2. 对于一次函数y=(m+4)x+2m-1，如果y随x增大而增大，且它的图象与y轴的交点在x轴下方，求m的取值范围。(6分)
3.
已知反比例函数
与一次函数y=－x＋2的图象交于A、B两点，若A点的坐标是(-2，4)，求点B的坐标。(6分)
4.
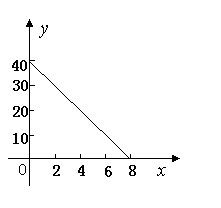如图是一辆汽车的剩油量y(升)与行驶时间x(小时)的图象，请根据图象回答下列问题：(共7分)
①、行驶前，汽车有_____升油。
②、汽车最多能行驶 小时，它每小时耗油____升。
③、行驶5小时后，汽车还有_____升油。
④、直接写出汽车剩油量y(升)与行驶时间x(小时)
的函数关系式，并指出x的取值范围。
5. 已知二次函数y＝ax2＋bx＋c的图象的顶点是(1，4)，且经过点(2，3)。求该二次函数的解析式。(7分)
四．综合解答题（每小题9分，共18分）
1.某商场销售一批衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取降价措施，经调查发现，若每件衬衫每降价1元，商场平均每天可以多售出2件．
(1).若每件降价x 元，每天盈利y 元，求y 与x 的关系式．
(2).每件衬衫降价多少元时，商场每天盈利最多？盈利多少元？
2.已知平面直角坐标系中的两点A(1，2)和B(0，3)，点C 在x轴上，且点C的横坐标是方程x2-2x-3=0的一个根。如果一个二次函数的图象经过 A、B、C 三点，求这个二次函数的关系式.