 初三数学月考试卷
初三数学月考试卷
出题人:萧小良
说明:全卷满分150分,时间120分钟
一、选择题(每小题4分,共40分。四个答案中只有一个是正确的)
1.一元二次方程x2+4x+3=0的两根是( )
A.x1=-1 ,x2=-3 B. x1=-1 ,x2=3
C.x1=1 ,x2=-3
D.
x1=1 , x2=3
2.已知3是关于x的方程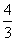 x2-2a+1=0的一个根,则2a等于( )
x2-2a+1=0的一个根,则2a等于( )
A.11 B.12 C.13 D.14
3.菱形的一个内角为60°,它所对的一条对角线长为4,则另一对角线的长为( )
A.8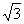 B.
4
B.
4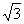 C.
2
C.
2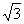 D.8
D.8
4.方程3(x +2)2 =1-2a无解,则a的范围为( )
A.a>1 B.a<1 C.a>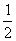 D.a<
D.a<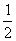

 5.有一等腰直角三角形纸片,以它的对称轴为折痕,将
5.有一等腰直角三角形纸片,以它的对称轴为折痕,将
 三角形对折,得到的三角形还是等腰直角三角形,依照
三角形对折,得到的三角形还是等腰直角三角形,依照
 上述方法将原等腰直角三角形折叠四次,所得小等腰直
上述方法将原等腰直角三角形折叠四次,所得小等腰直
 角三角形的周长是原等腰直角三角形周长的( )
角三角形的周长是原等腰直角三角形周长的( )
A.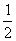 B.
B.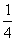 C.
C.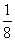 D.
D.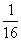
6.设方程 x2+x-1=0 的两个根分别为x1、x2,则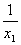 +
+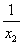 的值为( )
的值为( )
A.1 B.-1 C.
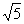
D.
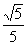


7.如图,在直角三角形ABC中,∠C=90°,∠BAC的

平分线AD交BC边于点D,CD=3,那么点D到直线

AB的距离是( )
A.1 B.2 C.3 D.4
8.已知方程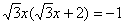 ,那么它的根的情况是( )
,那么它的根的情况是( )
A.没有实数根 B. 只有一个实数根
C.有两个相等的实数根 D.有两个不等的实数根
9. 菱形的一边和等腰直角三角形的一条直角边相等,菱形有一个内角等于
30°,则这两个图形的面积比为( )
A.1∶1 B.1∶2 C.1∶4
D.2∶1




10.(普通班做)如图,矩形ABCD中,AB=
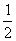
BC,

且DE=DC,则∠BCE=( )
A.15°
B.30°
C.45° D.60°





10.(重点班做)如图,正方形ABCD边长为1,F为
BC上一点,H为DC上一点,如果 FCH的周长
FCH的周长
为2,则∠HAF的度数为( )
A.15°
B.30°
C.45° D.60°

二、填空题(每小题4分,共20分)
11.直角三角形的两边为3、4,则周长为
。
12.方程3x2 -5x-2 = 0的两根之差的绝对值等于
13.既是轴对称图形又是中心对称图形的有
14.方程 2x2 +bx-3 = 0有一个根为2,则另一个根为

15.(普通班做)为了测量一个电线杆的高度,取一根2米长的竹竿放在阳光下,2米长的竹竿的影长为1米,并在同一时刻测得电线杆的影长为7.3米,则电线杆的高为
米。






15.(重点班做)如图,太阳在最低时光线与

水平线的夹角为30°,这时乙楼CD的影



子落在甲楼AB上的高EF为
米。
三、解答题(本题共50分)
16.用适当的方法解下列方程 (每小题5分,共10分)
(1) x2 -3x -18 = 0
(2) -2(x-3 )2 = x2-9
17.如图, ACB、
ACB、 ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F。请你在图中找出一对全等三角形,并写出证明它们全等的过程。(10分)
ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F。请你在图中找出一对全等三角形,并写出证明它们全等的过程。(10分)
18.(重点班做)我国大西北某县治理沙漠,绿化家乡是全县人民的共同愿望,到1998年底,全县沙漠的绿化率已达到30%,此后政府计划在近几年内,每年将当年初未被绿化的沙漠面积的m%栽上树进行绿化,到2000年底全县沙漠的绿化率已过43.3%,求m值。(10分)
(普通班做)党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001~2020年)要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x应为多少?(10分)
19.农民王伯伯有一口呈四边形的池塘,在它的四个角A,B,C,D处各有一棵大核桃树,王伯伯准备将池塘扩大一倍,又想保留核桃树不动,并要求扩建后的池塘成平行四边形形状,请问王伯伯能否实现这一设想?若能,请你设计并画出图形,再说明你的理由。 (10分)

 20.(普通班做)梯形上、下底的差为6,中位线的长为5,那么梯形的上底与下底的长分别是多少?(10分)
20.(普通班做)梯形上、下底的差为6,中位线的长为5,那么梯形的上底与下底的长分别是多少?(10分)
(重点班做)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm, BC=26cm. 一动点p从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P,Q分别从点A, 点C同时出发,当其中一点到达端点时,另一点也随之停止运动。设运动时间为t秒,则:(1) t为何值时,四边形PQCD为平行四边形?(2) t为何值时,四边形PQCD为等腰梯形?(10分)






四、证明题(共30分)
21.如图, ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(10分)
ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(10分)
(1)
求证:AE=CD
(2) 
 若AC=12, 求BD的长
若AC=12, 求BD的长
22. 如图,∠E=∠F=90°,∠B=∠C,AE=AF ,给出下列结论①∠1=∠2;②BE=CF;③CD=DN;④ΔACN≌ΔABM.其中正确的结论是什么?说明理由。(要找出所有正确的结论)(10分)




23.如图, ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F(10分)
ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F(10分)
(1)
求证:EO=FO;(普通班可以不做下两点)
(2)
当点O运动到何处时,四边形AECF是矩形?说明理由;
(3)
若AC边上存在点O,使四边形是正方形,∠B=60°,求AE∶BC的值。



五、 操作题(共10分)
24.如图,a、b分别代表铁路和公路。点M、N分别代表蔬菜和日杂货批发市场,现要建成一货物中转站P,使P到铁路和公路的距离相等,且P到两个批发市场的距离相等,请找出点P的位置,并写出作法。
a
·
b
·
























 25.请你画出这个几何体的三视图。
25.请你画出这个几何体的三视图。
 初三数学月考试卷
初三数学月考试卷 ![]() x2-2a+1=0的一个根,则2a等于( )
x2-2a+1=0的一个根,则2a等于( )![]() B.
4
B.
4![]() C.
2
C.
2![]() D.8
D.8 ![]() D.a<
D.a<![]()


![]() 5.有一等腰直角三角形纸片,以它的对称轴为折痕,将
5.有一等腰直角三角形纸片,以它的对称轴为折痕,将![]() 三角形对折,得到的三角形还是等腰直角三角形,依照
三角形对折,得到的三角形还是等腰直角三角形,依照![]()
![]()
![]() 上述方法将原等腰直角三角形折叠四次,所得小等腰直
上述方法将原等腰直角三角形折叠四次,所得小等腰直![]() 角三角形的周长是原等腰直角三角形周长的( )
角三角形的周长是原等腰直角三角形周长的( )![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() +
+![]() 的值为( )
的值为( )
![]() ,那么它的根的情况是( )
,那么它的根的情况是( ) ![]()
![]() FCH的周长
FCH的周长 15.(普通班做)为了测量一个电线杆的高度,取一根2米长的竹竿放在阳光下,2米长的竹竿的影长为1米,并在同一时刻测得电线杆的影长为7.3米,则电线杆的高为 米。
15.(普通班做)为了测量一个电线杆的高度,取一根2米长的竹竿放在阳光下,2米长的竹竿的影长为1米,并在同一时刻测得电线杆的影长为7.3米,则电线杆的高为 米。
![]() ACB、
ACB、![]() ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F。请你在图中找出一对全等三角形,并写出证明它们全等的过程。(10分)
ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F。请你在图中找出一对全等三角形,并写出证明它们全等的过程。(10分)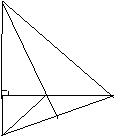

 20.(普通班做)梯形上、下底的差为6,中位线的长为5,那么梯形的上底与下底的长分别是多少?(10分)
20.(普通班做)梯形上、下底的差为6,中位线的长为5,那么梯形的上底与下底的长分别是多少?(10分)![]()
![]()
![]() ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(10分)
ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(10分)

![]() 若AC=12, 求BD的长
若AC=12, 求BD的长


![]() ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F(10分)
ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F(10分)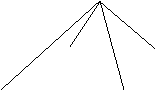
![]()
![]()
![]()

 a
a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 25.请你画出这个几何体的三视图。
25.请你画出这个几何体的三视图。