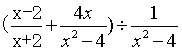初三数学中考模拟试卷
姓名___________得分___________
HI，亲爱的同学，你好！今天是展示你才能的时候了，只要你仔细审题、认真答题，把平常的水平发挥出来，你就会有出色的表现，放松一点，相信自己的实力！
一、细心选一选(10×2=20分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.化简
的结果是( )
A. 
B.－
C. 
D. 
2.如果分式
的值为零,那么x等于(
)
A.－1 B.1 C.－1或1 D.1或2
3.方程x2 = 2x的解是( )
A、x=2 B、x1=
，x2= 0 C、x1=2，x2=0 D、x = 0
4.用换元法解方程(x2＋x)2＋(x2＋x)＝6时，如果设x2＋x＝y，那么原方程可变形为( )
A、y2＋y－6＝0 B、y2－y－6＝0 C、y2－y＋6＝0 D、y2＋y＋6＝0
5.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整个挂图的面积是5 400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1 400=0 B.x2+65x－350=0
C.x2-130x-1 400=0 D.x2-64x-1 350=0
6.半径为1的圆中，圆心角为120°的扇形面积为 （ ）
（A）
（B）
（C）
（D） 
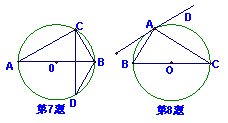
7.如图，已知AB是⊙O的直径，CD是弦且CD⊥AB，
BC＝6，AC＝8，则sin∠ABD的值是（ ）
（A）
（B）
（C）
（D）
8.如图，已知BC是⊙O的直径，AD切⊙O于A，
若∠C=40°，则∠DAC=（ ）
（A）50°（B）40° （C）25° （D）20°
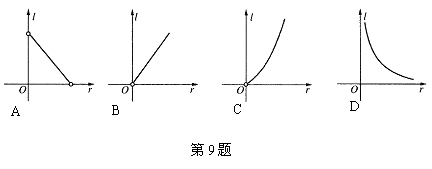
9.如果一个圆柱的侧面积为16，那么这个圆柱的高l与底面半径r之间函数关系的大致图象是( )
 |
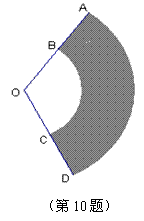
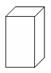
10.如图，将图中的阴影部分剪下来，围成一个几何体的侧面，使AB、DC重合，则所围成的几何体图形是( )
 |
 |
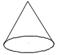
（A） （B）
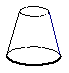（C） （D）
二、专心填一填(10×2=20分)
11.已知a+
=5,则
=________.
12.已知x=
+1,则代数式
的值为___________.
13.“在三角形中至少有一个角不大于60°”用反证法来证明时,第一步应假设:_______________________________________________
14. 一只不透明的布袋中有三种小球（除颜色以外没有任何区别），分别是2个红球，3个白球和5个黑球，每次只摸出一只小球，观察后均放回搅匀．在连续9次摸出的都是黑球的情况下，第10次摸出红球的概率是 ．
15.某超级市场失窃，大量的商品在夜间被罪犯用汽车运走。三个嫌疑犯被警察局传讯，警察局已经掌握了以下事实：(1)罪犯不在A、B、C三人之外；(2)C作案时总得有A作从犯；(3)B不会开车。在此案中能肯定的作案主犯是＿＿＿
16.如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=
，且DE=1则边BC的长为_____________。
|
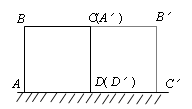
17.如图，一块边长为10cm的正方形木板ABCD，在水平桌面上绕点D按顺时针方向旋转到A′B′,C′D′的位置时，顶点B从开始到结束所经过的路径长为______________.
18.老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：甲：函数的图象经过第一象限；乙：函数的图象经过第三象限；丙：在每个象限内，y随x的增大而减小．请你根据他们的叙述构造满足上述性质的一函数 ________．
19.已知开口向上的抛物线y=a(x+2)(x－8)与x轴交于A,B两点,与y轴交于C点，若∠ACB=90°,则a=_______.
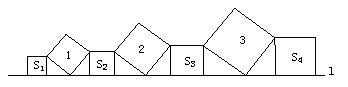
20.在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_____________。
|
21. (10分)有一道题“先化简，再求值：，
其中
。”
小玲做题时把“”错抄成了
“
”，但她的计算结果也是正确的，请你解释这是怎么回事？
22. (10分)已知关于x的一元二次方程x2－(k＋1) x－6=0的一个根是2，
求方程的另一根和k的值
|
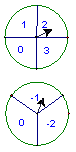
被分成4等份、3等份，并在每份内均标有数字，如图所示。
王扬和刘菲同学用这两个转盘做游戏，游戏规则如下：
①分别转动转盘A与B；
②两个转盘停止后，将两个指针所指份内的数字相加（如果
指针恰好停在等分线上，那么重转一次，直到指针指向某一
份为止）。③如果和为0，王扬获胜；否则刘非获胜。
（1） 用列表法（或树状图）求王扬获胜的概率；
（2） 你认为这个游戏对双方公平吗？请说明理由。
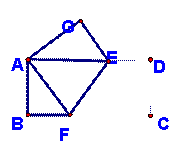
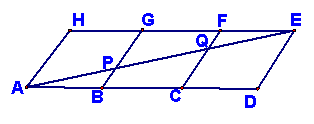
24. (10分)如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，
（1） 若AB=6，求线段BP的长；（6分）
（2） 观察图形，是否有三角形与ΔACQ全等？并证明你的结论，（4分）
|
|
26. (10分)已知线段AC=8，BD=6．
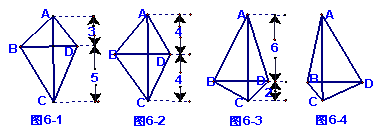（1）已知线段AC垂直于线段BD．设图6—1、图6—2和图6—3中的四边形ABCD的面积分别为S1，S2和S3，则S1=
，S2=
，S3=
；
（2）如图6—4，对于线段AC与线段BD垂直相交(垂足O不与点A，C，B，D重合)的任意情形，请你就四边形ABCD面积的大小提出猜想，并证明你的猜想；
（3）当线段BD与AC（或CA）的延长线垂直相交时，猜想顺次连接点A，B，C，D，A所围成的封闭图形的面积是多少？
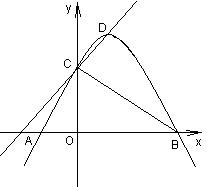
27.（10分） 如图，已知二次函数
的图像与x轴交于点A、点B（点B在X轴的正半轴上），与y轴交于点C，其顶点为D，直线DC的函数关系式为
，又tan∠OBC=1，
（1） 求a、k的值；（4分）
（2） 探究：在该二次函数的图像上是否存在点P（点P与点B、C补重合），使得ΔPBC是以BC为一条直角边的直角三角形？若存在，求出点P的坐标，若不存在，请你说明理由（6分）
解： 