初三数学中考模拟试题
一、 选择题(本题有12小题,共36分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
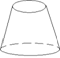
1.下列空间图形中是圆柱的为( )

![]()
![]()
(A) (B) (C) (D)
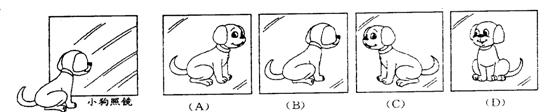 2.一只小狗正在平面镜前欣赏自己的全身像,此时,它所看到的全身像是( )
2.一只小狗正在平面镜前欣赏自己的全身像,此时,它所看到的全身像是( )
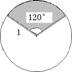 3.如图,半径为1的圆中,圆心角为120°的扇形面积为 ( )
3.如图,半径为1的圆中,圆心角为120°的扇形面积为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
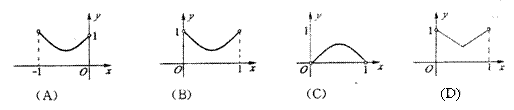
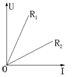 4.阻值为
4.阻值为![]() 和
和![]() 的两个电阻,其电压
的两个电阻,其电压![]() 关于电流强度
关于电流强度![]() 的函数图象如图,则( )
的函数图象如图,则( )
(A)![]() >
>![]() (B)
(B)![]() <
<![]() (C)
(C)![]() =
=![]() (D)以上均有可能
(D)以上均有可能
5.一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
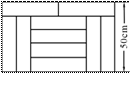 6.
如图,宽为50 cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为( )
6.
如图,宽为50 cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为( )
A. 400 cm2 B. 500 cm2
C. 600 cm2 D. 4000 cm2
7、计算![]() 的结果应是( )
的结果应是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
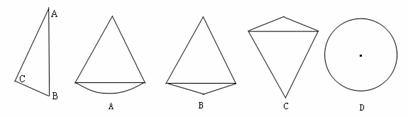 8、将左图所示放置的一个Rt△ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图形中的(
)
8、将左图所示放置的一个Rt△ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图形中的(
)
9、下列调查的样本具有代表性的是( )
A、调查一个班级里座位号为3的倍数的学生对新数学老师工作态度的评价;
B、在疗养院里调查我国老年人的健康情况;
C、在大学生中调查我国青年业余时间娱乐的主要方式;
 D、到别墅区去调查我国普通居民的生活水平;
D、到别墅区去调查我国普通居民的生活水平;
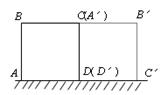
10、如图,一块边长为10cm的正方形木板ABCD,在
水平桌面上绕点D按顺时针方向旋转到A′B′
C′D′的位置时,顶点B从开始到结束所经过
的路径长为( )
(A)20cm (B)20![]() cm (C)10πcm (D)5
cm (C)10πcm (D)5![]() πcm
πcm

|
![]()
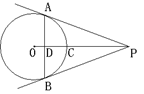 12.如图,PA
、PB是⊙O的切线,A、
B 为切点,OP交AB于点D,交⊙O于点C
, 在线段AB、PA、PB、PC、CD中,已知其中两条线段的长,但还无法计算出⊙O直径的两条线段是( )
12.如图,PA
、PB是⊙O的切线,A、
B 为切点,OP交AB于点D,交⊙O于点C
, 在线段AB、PA、PB、PC、CD中,已知其中两条线段的长,但还无法计算出⊙O直径的两条线段是( )
|
二、填空题(本题有8小题,共24分.)
 13.试写出图象位于第二象限与第四象限的一个反比例函数解析式
.
13.试写出图象位于第二象限与第四象限的一个反比例函数解析式
.
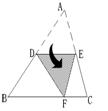
14.如图,D、E为△ABC两边AB、AC的中点,将△ABC沿线段DE折叠,
使点A落在点F处,若∠B=55°,则∠BDF= °.
15、装修工人拟用某种材料包装圆柱体的石柱侧面,现量得石柱底面周长为0.9m,柱高约为3m,那么至少要用该种材料_______________m2.
16.在平面内有线段AB和直线l,点A、B到直线l的距离分别是4cm、6cm.则线段AB的中点C到直线l的距离 .
17.已知下列等式:
① 13=12;
② 13+23=32;
③ 13+23+33=62;
④ 13+23+33+43=102 ;
…… ……
由此规律知,第⑤个等式是 .
18、生物学研究表明:某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6cm时,蛇长为45.5cm;当尾长为14cm时,蛇长为105.5cm,当一条蛇的尾长为10cm时,这条蛇的长度是__________cm。
 19.某种药品的说明书上,贴有如右所
19.某种药品的说明书上,贴有如右所
示的标签,一次服用这种药品的剂
 量范围是
量范围是 ![]() ~
~ ![]()
20.如图,把矩形ABCD沿EF折叠,使点C落在点
A处,点D落在点G处,若∠CFE=![]() ,且DE=1,
,且DE=1,
则边BC的长为_____________。
三、解答题(21~24每题9分,25~28每题10分,29题14分。)
21、计算:-12005-(1+0.5)×3-1÷(-2) 2+(cos60°-![]() )0
)0
22、已知实数a满足a2+2a-8=0,求![]() 的值.
的值.
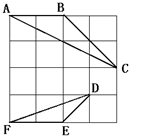 23、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC= °,BC=
;
23、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC= °,BC=
;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
 24、如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,则
BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)【参考数据:
24、如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,则
BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)【参考数据:![]() 】
】
25、如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
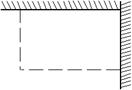 (1)设矩形的一边为
(1)设矩形的一边为![]() (m),面积为
(m),面积为![]() (m2),求
(m2),求![]() 关
关
于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?
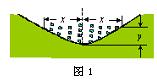 26、如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
26、如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
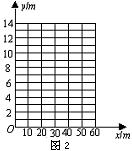 (1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:

②根据所填表中数据的规律,猜想出用x表示y 的二次函数的表达式为____________。
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?
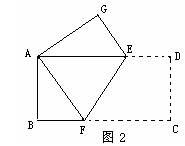
27、下面让我们来探究有关材料的利用率问题:工人师傅要充分利用一块边长为100㎝的正三角形簿铁皮材料(如图1)来制作一个圆锥体模型(制作时接头部分所用材料不考虑)。
(1)求这块三角形铁皮的面积(结果精确到0.01㎝2);
(2)假如要制作的圆锥是一个无底面的模型,且使三角形铁皮的利用率最高,请你在图2中画出裁剪方案的草图,并计算出铁皮的利用率(精确到1%);
(3)假如要用这块铁皮裁一块完整的圆形和一块完整的扇形,使之配套,恰好做成一个封闭圆锥模型,且使铁皮得到充分利用,请你设计一种裁剪方案,在图3中画出草图,并计算出铁皮的利用率(精确到1%)。
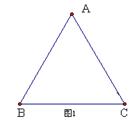 |  |  | |||
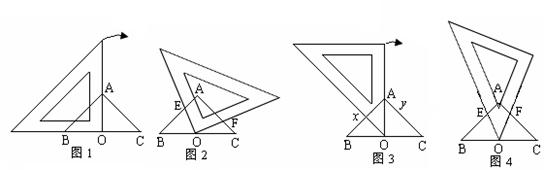 28、在△ABC中,AB=AC=2,∠A=90°,取一块含45°角的直角三角形尺,将直角顶点放在斜边BC边的中点O处,顺时针方向旋转(如图1);使90°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图2),设BE=
28、在△ABC中,AB=AC=2,∠A=90°,取一块含45°角的直角三角形尺,将直角顶点放在斜边BC边的中点O处,顺时针方向旋转(如图1);使90°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图2),设BE=![]() ,CF=
,CF=![]() 。
。
(1)求![]() 与
与![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(2)将三角尺绕O点旋转的过程中,△OEF是否能成为等腰直角三角形?若能,请证明你的结论;
(3)若将直角三角形尺45°角的顶点放在斜边BC边的中点O处,顺时针方向旋转(如图3),其它条件不变。
①试直接写出![]() 与
与![]() 的函数解析式,及
的函数解析式,及![]() 的取值范围;
的取值范围;
②将三角尺绕O点旋转(图4)的过程中,△OEF是否能成为等腰三角形?若能,求出△OEF为等腰三角形时![]() 的值;若不能,请说明理由。
的值;若不能,请说明理由。
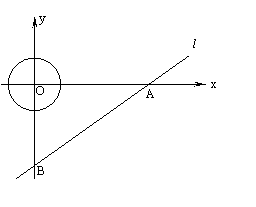
29、已知:如图所示,直线l的解析式为 y=![]() x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.
(1) 求A、B两点的坐标;
(2) 一个圆心在坐标原点、半径为1的圆,以0.4个单位/秒的速度向x轴正方向运动,问在什么时刻该圆与直线l相切;
(3) 在题(2)中,若在圆开始运动的同时,一动点P从B点出发,沿BA方向以0.5个单位/秒的速度运动,问在整个运动过程中,点P在动圆的圆面(即圆上和圆的内部)内一共运动了多长时间?
 |