课改地区
初中毕业、升学考试数学卷
《满分:120分 考试时间:120分钟》
一、填空题(每空2分，共32分)
1. (-3)2 的相反数是 ______
2. 4320″等于 ________ 度.
3. 对代数式
作合理的解释是 ________
4. 为大力支持少数民族地区的经济建设和社会繁荣，1998年以来，国家安排5个民族自治区的国债投资累计达1117.3亿元. 这个数据精确到百亿位，并用科学记数法表示为 ___________ 元，它有 ______ 个有效数字.
5. 一次函数y=(k+1)x+k-2的图像经过一、三、四象限，则k的取值范围是 ________
6. 已知点A(3，n)关于y轴对称的点的坐标为(-3，2)，那么n的值为 _______ ，点A关于原点对称的点的坐标是 ________
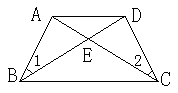7. 如图，已知∠1=∠2，要使△ABE≌△DCE, 还应添加的一个条件
是 ____________ ，
由此还可以得到的一
个关于三角形全等的
结论是 _______
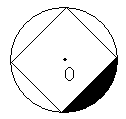
8. 如图，正方形内接于⊙O，
已知正方形的边长为
cm，
则图中的阴影部分的面积
是 _______ cm2(用π表示).
9. 下表是对某校10名女生
进行身高测量的数据表(单位: 厘米)， 但其中一个数据不慎丢失(用x表示).
| 身高(cm) | 156 | 162 | x | 165 | 157 |
| 身高(cm) | 168 | 165 | 163 | 170 | 159 |
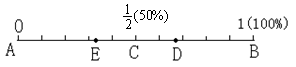从这10名女生中任意抽出一名，其身高不低于162cm的事件的可能性，可以用下图中的点 ______ 表示(在A、B、C、D、E五个字母中选择一个符合题意的)
10.
分解因式: 
________
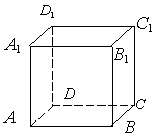
11. 如图，已知正方体的
棱长为2，则正方体表面
上从A点到C1点的最短
距离为 ________
12. 一化工厂生产某种
产品，产品出厂价为500
元/吨，其原材料成本(含设备损耗)为200元/吨，同时，生产1吨该产品需付环保处理费及各项支出共计100元.写出利润y(元)与产品销量x(吨)之间的函数关系式 _________ ，销售该产品 ________ 吨，才能获得10万元利润.
二、选择题(每小题3分，共24分，每小题给出的四个选项中，只有一个选项符合要求)
13. 如图，是一个由若干个相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体的个数是 ( )
 |  |  | |||
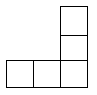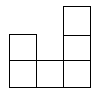主视图 左视图 俯视图
A.7个 B.8个 C.9个 D.10个
14. 方程组 
的解是 （
）
A. 
B. 
C. 
D.
15. 把不等式组
的解集表示在数轴上，正确的是
( )
 |  | ||
A. B.
 | |||
 | |||
C. D.
16. 某校10名学生四月份参加西部环境保护实践活动的时间(小时)分别为: 3，3，6，4，3，7，5，7，4，9，这组数据的众数和中位数分别为
A. 3和4.5 B. 9和7
C. 3和3 D. 3和5
17. 反比例函数 
与正比例函数y=2kx
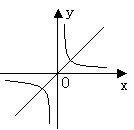
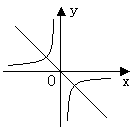在同一坐标系中的图像不可能是 （ ）
A. B.
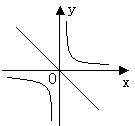
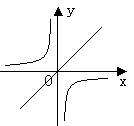
C. D.
18. 下列图形中既是轴对称图形又是中心对称图形的是 （ ）
A. B. C. D.
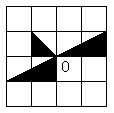19.
在图中，将左边方格纸
中的图形绕O点顺时针旋
转90°得到的图形是
（ ）
 |  | ||
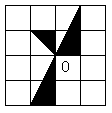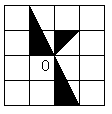A. B.
 |  | ||
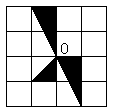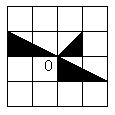C. D.
20. 均匀的正四面体的各面上依次标有1，2，3，4四个数字，同时抛掷两个这样的正四面体，着地的一面数字之和为5的概率是 ( )
A.
B.
C.
D.
三、解答题(本题共8小题，第21，22题每题7分，第23～26题每题8分，第27，28题每题9分，共64分)
21. 计算:
22. 作图题(本题有两个小题，第(1)题5分，第(2)题2分. 利用尺规，按下列要求作图，不写作法，但要保留作图痕迹)
(1) 在图中作出AB的中点M; 作出∠BCD的平分线CN; 延长CD到P，使DP=2CD.
(2) 如图，是一个破损的机器部件，它的残留边缘是圆弧，请作图找出圆弧所在圆的圆心.
23. 某市一所中学为了解学生每天的消费情况，随机抽取了该校30名学生进行调查，并将调查结果记录如下: 0～5元，有14人，占46.6%;
6元～10元，有6人，占 %;11元～15元，有5人，占16.7%; 16元～20元，有 人，占10%; 20元以上(不包括20元)，有2人，占6.7%
(1) 根据题意把上述 中所缺数据补充完整
(2) 请选择题中适当数据，设计一个反映设校学生每天消费情况的统计图
(3) 你从(2)的统计图中获得了什么信息? (只写一条)
24. 近年来， 国家为了加快贫困地区教育事业的发展步伐，进一步解决贫困地区学生上学难的问题，实行了“两免一补”政策，收到了良好效果.某地在校学生比原来增加了4217名，其中小学在校生增加了10%，初中在校生增加了23%，现在校中小学生共有32191名. 求该地原来在校中小学生各有多少人?
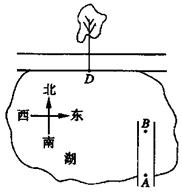
25. 如图，一人工湖的对岸有一条笔直的小路，湖上原有一座小桥与小路垂直相通，现小桥有一部分已断裂，另一部分完好. 站在完好的桥头A测得路边的小树D在它的北偏西30°，前进32米到断口B处，又测得小树D在它的北偏西45°，请计算小桥断裂部分的长(结果用根号表示).
 |
26. 某种化肥在县城里的甲、乙两个生产资料门市部均有销售，现了解到该种化肥在甲、乙两个门市部的标价均为600元/吨， 但都有一定的优惠政策，甲门市部是第一吨按标价收费，超出部分每吨优惠25%; 乙门市部每吨优惠20%出售.
(1) 写出甲门市部每次交易的销售额y1(元)与销量x(吨)之间的函数关系式及乙门市部每次交易的销售额y2(元)与销量x(吨)之间的函数关系式.
(2) 种粮大户张某想一次购买此种化肥4吨，李某想一次购买此种化肥8吨，他们到哪个门市部购买省钱，请给他们分别提出合理建议.
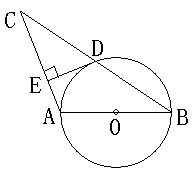
27. 如图，已知AB是⊙O的直径，⊙O过BC的
中点D，且DE⊥AC.
(1) 求证: DE是⊙O的切线;
(2) 若∠C=30°，CD=10cm，求⊙O的半径.
 |
28. 二次函数y=ax2+bx+c (a≠0) 的图像经过点A(3，0)，B(2，-3)，并且以x=1为对称轴.
(1) 求此函数的解析式;
(2) 作出二次函数的大致图像;
(3) 在对称轴x=1上是否存在一点P，使△PAB中的PA=PB，若存在，求出P点的坐标，若不存在，说明理由.