初中毕业班教学质量检查
数 学 试 题
一、填空题：（每小题3分，共36分）
1、―3的相反数是 。
2、分解因式：
。
3、泉州市委、市政府在2006年5月出台的《关于引进高层次人才的若干规定》中提出。中国科学院院士、中国国工程院院士带项目来我市工作的可获得800000元奖励，用科学记数法表示为 元。
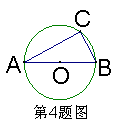
4、如图，AB为⊙O的直径，点C在⊙O上，∠B=50°，则∠A= 度。
5、初三年一班有7名同学参加参加学校举行的体育测试
（成绩单位：分），成绩分别是87，90，87，89，91，
88，87。则它们成绩的众数是 。
6、一元一次方程
的解是
。
7、在函数
中，自变量x的取值范围是
。
8、点P（3，2）关于原点对称的点的坐标为（ ）。
9、已知圆锥的底面半径为3cm，母线长为4cm，
则该圆锥的侧面展开图的面积为 cm2。
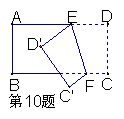
10、如图，把一个长方形纸片沿EF折叠后，点D、C分别落
在D′、C′的位置，若∠EFB=65°，则∠AE D′= 度。
11、样本2，2，3，5的方差等于 。
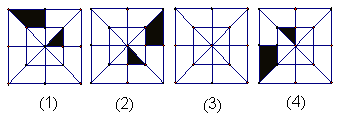
12、分析图①，②，④中阴影部分的变化规律，按此规律在图③中画出其中的阴影部分。
二、选择题：（每小题4分，共24分）
13、计算：
的结果是（ ）A、
B、
C、
D、
14、同时抛掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能事件的是（ ）
A、点数之和为10； B、点数之和小于5；
C、点数之和大于3且小于9； D、点数之和为14；
15、右边几何体的府视图是（ ）
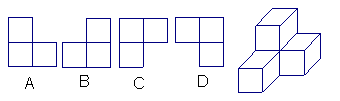
16、下列调查中，比较适合用普查而不适合抽样调查方式的是（ ）
A、调查一批显像管的使用寿命；B、调查“永春芦柑”的甜度和含水量；
C、调查我县居民的环保意识； D、调查你所在学校数学教师的年龄状况。
17、下列四个命题中，假命题的是（ ）
A、对角线互相平分的四边形是平行四边形；B、三点确定一个圆；
C、圆既是轴对称图形，又是中心对称图形；D、三角形的内角和等于180度。
18、三峡峡工程下闸蓄水期间，水库水位由106米升至135米用了10天的时间，高峡出平湖初现人间，假设水库水位匀速上升，那么图中，能正确反映这10天水位h（米）随时间t（天）变化的是（ ）
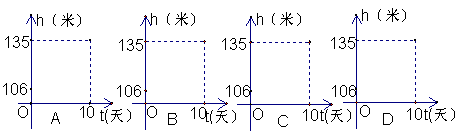
二、解答题：（共90分）
19、（8分）计算：
20、（8分）先化简下列代数式，再求值：
，其中
。
21、（8分）如图，在
ABCD中，AE⊥BD，CF⊥BD。垂足分别为E、F。
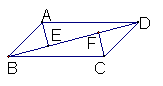求证：△ABE≌△CDF.
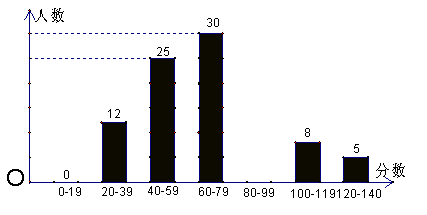22、（8分）阳光中学举行应用数学知识竞赛。已知竞赛成绩都是整数，试题满分为140分，现从参赛学生中随机抽取100名学生的成绩进行统计分析，得到如下图：（1）将统计图补充完整；（2）竞赛成绩的中位数落在 分数段内；
（3）若共有500名学生参加本次竞赛，请你用样本估计总体的统计思想，写出一条信 。
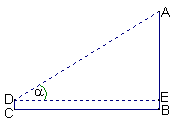
23、（8分）如图，在与旗杆AB相距20米的C处，用1.2米的测角仪CD测得旗杆顶端的仰角
，求旗杆AB的高（精确到0.1米）
24、（8分）A袋中有2个红球和1个白球，B袋中有1个红球和2个白球（这些球除颜色外没有其它区别），甲、乙两人分别从A、B袋中各摸出一个球。游戏规定，两个小球颜色相同时，甲获胜；两个小球颜色不同时，乙获胜。
（1）用列表法（或画树状图）求甲获胜的概率；
（2）你认为这个游戏公平吗？请简要说明理由。
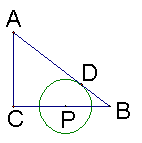
25、（8分）在Rt△ABC中，∠C=90°，AC=3，BC=4。
（1）求AB的长；（2）如图，已知P为BC的中点，以P为圆心的⊙P与AB相切于点D。若以C为圆心的⊙C与⊙P相切，求⊙C的半径。
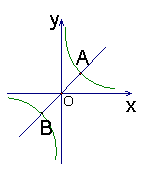
26、（8分）如图，正比例函数
的图象与反比例函数
的图象相交于A、B两点，且A的坐标为（1，1）。（1）求正比例函数的解析式；
（2）已知M，N是y轴上的点，若四边形AMBN是矩形，求M、N的坐标。
27（13分）一位水果销售商到果园购买荔枝和芒果，果园用两种规格不同的硬纸箱分别包装荔枝和芒果。
（1）设每箱芒果的销售利润为x元，且每箱荔枝的销售利润比每箱芒果多7元，则每箱荔枝的销售利润为 元（用含x的代数式表示）。
（2）在（1）的条件下，该销售商第一次进货荔枝26箱，芒果18箱，售完后共获利534元，求每箱荔枝、芒果的销售利润各是多少元；
（3）在（2）的条件下，销售商租用一辆车再次进货（已知这辆车完全装荔枝最多能装40箱，完全装芒果最多能装70箱），计划所购荔枝的箱数是芒果箱数的3倍少3箱，且售完后所获的利润不少于500元，销售商怎样进货获利最多？
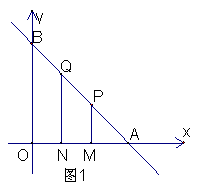
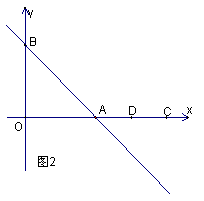
28、（13分）函数
与x轴交于点A，与y轴交于点B，动点M在x轴的正半轴上，N为OM的中点，过M、N分别作x轴的垂线，交直线于点P、Q，设N点的坐标为（x，0）。
（1）直接写出M点的坐标（ ， ）；
（2）如图1，若点M在线段OA上运动，用含x的代数式表示四边形MPNQ的面积；
（3）如图2，已知C（8，0），D为AC的中点，若点M在线段CD（含线段的端点）上运动，求线段MP、NQ与直线、x轴所围成的图形的面积的最大值。
四、附加题：（共10分）
友情提示：请同学们做完上面的考题后，再认真检查一遍，估计一下你的得分情况。如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题得分不计入全卷总分。
1、（5分）某地区夏季一周内每天的最高气温（单位：°C）分别是：35，33，31，34，31，37，32，求这组数据的极差。
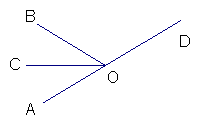
2、（5分）如图，已知O是直线CD上的点，OA平分∠BOC，∠AOC=35°，则∠BOD的度数。
