初三数学推荐考试试卷

初三数学推荐考试试卷

　　　　　　　　　　　　　　　　　　　

一、选择题：（每小题2分，共20分）

1.下列各式中，正确的是　　　　　　　　　　　　　　　　　　　　　　　  （　　 ）　　　　　　　　　　　　　　　　　

A.　 B.　 C.　 D.

2.若＜1是不等式的解集，则的取值为　　　　　　  （　　 ）

　A.a＞3　　　　  B.a＝3　　　　C.a＜3　　　　  D.a＝4

3.已知线段,求作线段,使　　　, 下列作法中正确的是　　　　　　　 （　　 ）

4.一个梯形ABCD的两腰AD和BC延长相交于E，若两底的长度分别是12和8，梯形ABCD的面积等于90，则△DCE的面积为　　　　　　　　　　　　　　　　　　  （　　 ）

　A.50　　　　　  B.64　　　　　  C.72　　　　　　  D.54

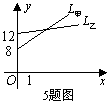
5.如图,、分别是甲、乙两弹簧的长cm与所挂物体质量kg

之间函数关系的图像，设甲弹簧每挂1kg物体伸长的长度为cm ，

乙弹簧每挂1kg物体伸长的长度为cm，则与的关系是（　　 ）

A.＞ 　 B.＝ 　 C.＜ 　　D.不能确定

6.一等腰直角三角形的内切圆与外接圆的半径之比为　　　　 （ 　　）

　　A.　　 B.　　　C.＋1　　　D.－1

7.下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　 （　 　）

A.为了检验一批零件的质量，从中抽取10件，在这个问题中，10是抽取的样本

B.如果、、…、的平均数是，那么样…

C.8、9、10、11、11这组数的众数是2

D.一组数据的标准差是这组数据的方差的平方

8.下列说法中，正确的个数有　　　　　　　　　　　　　　　　　　　　　 （　　 ）

(1)经过三点可以作一个圆　　　　　 

(2)两圆的半径分别为3 cm和4 cm，圆心距为 1 cm，则这两圆的位置关系是外切

(3) 相交两圆的公共弦垂直平分两圆的连心线　

(4) 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧

A.0个　　　　 B.1个　　　　  C.2个　　　　  D.3个

9. 不等式kx+b＞0的解集是x＞4，点（b，1）在双曲线上，则一次函数的图像不经过的象限是　　　　　　　　　　　　　　　 （　　 ）

A.第一象限　　B.第二象限 　 C.第三象限　　D.第四象限

10.小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不　　　　　

同的布料生产一批形状如图所示的风筝，点E，F，G，　　　　 

H分别是四边形ABCD各边的中点.其中阴影部分用甲布　

料，其余部分用乙布料（裁剪两种布料时，均不计余料）.

若生产这批风筝需要甲布料30匹，那么需要乙布料(　　　)

A．15匹　　　　　　　　  B．20匹　　

C．30匹　　　　　　　　  D．60匹

二、填空题：（每小题3分，共24分）

11.计算：＝　　　　　  .

12.分解因式：＝　　　　　　　　　　　　　　　　　　  .

13.某商场销售一批电视机，一月份每台毛利润是售出价的20％（毛利润＝售出价－买入价），二月份该商场将每台售出价调低10％（买入价不变），结果销售台数比一月份增加120％，那么二月份的毛利润总额与一月份毛利润总额的比是　　　　  .

14.如图,等边△ABC的边长为2cm，以BC为直径的半圆O分别交AB、AC于点E、F，那么由线段AE、AF及弧EF围成的弓形面积S＝　　　　　cm².

15.如图,在△ABC中，AD是BC边上的中线，F是AD上一点，且AF∶FD＝1∶5，连结CF并延长交AB于E，若AC＝15cm，则BE＝　　　　  cm.

　　　

14题图　　　　　　　　　  15题图　　　　　　　　　  17题图　　　　　

16.关于的方程的两实数根互为倒数，则k＝　　　　.

17.如图,已知AP平分∠BAC，过P点的切线交AC的延长线于D，如果AB＝3cm，AD＝6cm，那么AP＝　　　　 .

18.观察下面各组数：（3，4，5）、（5，12，13）、（7，24，25）、（9，40，41）、…，可发现：4=，12=，24=，…，若设某组数的第一个数为，则这组数为（，　　　　　  ，　　　　　　  ）．

三、解答题：（每小题10分，共40分）

19.解方程：

20.已知：如图,点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，

且EA⊥AF.

　求证：DE＝BF

21.如图，直线y=-2x+2与x轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D.

（1）求点A、B的坐标和AD的长；

（2）求过B、A、D三点的抛物线的解析式.

22.为了普及环保知识，增强环保意识，某中学组织了环保知识竞赛活动，

　　初中三各年级根据初赛成绩分别选出了10名同学参加决赛，这些选手的决赛成绩（满分为100分）如下表所示：

	决赛成绩（单位：分）
初一年级	80　 86　 88　 80　 88　 99　 80　 74　 91　 89
初二年级	85　 85　 87　 97　 85　 76　 88　 77　 87　 88
初三年级	82　 80　 78　 78　 81　 96　 97　 88　 89　 86

（1）请你填写下表：

	平均分	众数	中位数
初一年级	85.5		87
初二年级	85.5	85
初三年级			84

（2）请从以下两个不同的角度对三个年级的决赛成绩进行分析：

　　①从众数和平均数相结合看（分析哪个年级成绩好些）；

　　②从平均数和中位数相结合看（分析哪个年级成绩好些）.

（3）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强些？并说明理由.

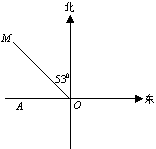23.某校A位于工地O的正西方向，且OA＝200m，一辆货车从O点出发，以每秒5米的速度沿北偏西53⁰方向行驶，已知货车的噪声污染半径为130m，试问学校是否在货车噪声污染范围内？若不在，请说明理由；若在，求出学校受噪声污染的时间有几秒？（已知sin53⁰＝0.80，sin37⁰＝0.60，tan37⁰＝0.75）

24.已知：二次函数的图象与轴交于点C.

（1）求证：二次函数的图象与轴必有交点；

（2）当二次函数的图象与轴正、负方向各有一个交点，分别为A（x₁，0）、

B（x₂，0），且AB =3时，求点C的坐标.

25.如图，H是⊙O的内接锐角△ABC的高线AD、BE的交点，过点A引⊙O的切线与BE的延长线相交于点P，若AB的长是关于x的方程x²-6x+36(cos²C-cosC+1)=0的实数根.

（1）求：∠C=_______度；AB的长等于_______（直接写出结果）

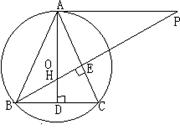（2）若BP=9，试判断△ABC的形状，并说明理由.

26.某家庭新购住房需要装修，如果甲、乙两个装饰公司合做，12天可以完成，需付装修

费1.04万元；如果甲公司先做9天，剩下的由乙公司来做，还需16天完成，共需付

装修费1.06万元．若只选一个装饰公司来完成装修任务，应选择哪个装饰公司？试说

明理由．

四、解答题：

27.如图1，梯形ABCD中，AD//BC，AD⊥DC，M为AB的中点.

（1）求证：MD=MC；

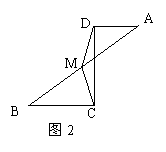（2）平移AB使AB与CD相交，且保持AD//BC与 AD⊥DC，M仍为AB的中点（如图2），试问（1）的结论是否仍然成立？请证明你的结论.

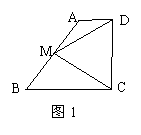
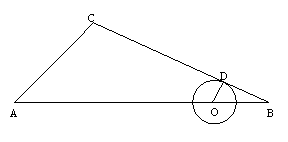
28．如图，四边形ABCD内接于以BC为直径的半圆，圆心为O，且AB＝AD，延长CB、DA

交于P，过C点作PD的垂线交PD的延长线于E，当PB＝BO，CD＝18时，

求：（1）⊙O的半径长；（2）DE的长

29.如图，在△ABC中，AB=17，AC=5，∠CAB=45°，点O在BA上移动，以O为圆心作⊙O，使⊙O与边BC相切，切点为D，设⊙O的半径为x，四边形AODC的面积为y．

　 ⑴ 求 y与x的函数关系式,并求x的取值范围；

　 ⑵当x为何值时，⊙O与BC、AC都相切？

　

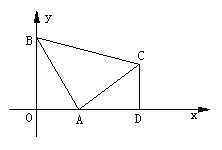
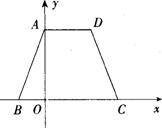
30. 已知：如图，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6），且AB＝.

（1）求点B的坐标；

（2）求经过A、B、D三点的抛物线的解析式；

（3）在（2）中所求的抛物线上是否存在一点P，使得?若存在，请求出该点坐标，若不存在，请说明理由.