初三数学专题复习大题归类（一）
注意：本卷共有7题。供初三毕业生复习用，可以选做。
二次函数综合类
1．抛物线y=1/8x2=3mx+18m2-m与x轴交于A（x1,0）和B（x2，0）两点（其中x1<x2），与y轴交于点C（0，b）。
y
1．
求m的取值范围；
2．
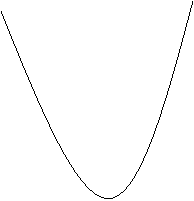若m>1/18，且OA+OB=3OC，
求：抛物线的解析式及A、B
和C的坐标；
3． 在（2）的条件下，点P、Q C
分别从A、O两点同时出发
并以相同的速度沿AB、OC
Q
向B、C运动，连接PQ交
BC于点M。设AP=k，问： A P B O x
是否存在k值，使以P、M、
B为顶点的三角形与△ABC
相似？若存在，请求出k的
值；若不存，在请说明理由。
（第1题图）
初中（2005）专题训练 共4页 第1页
2．已知二次函数y=x2 +ax+a-2。
（1） 证明：不论a取何值时，抛物线的顶点Q总在x轴下方；
（2） 设抛物线y=x2+ax+a-2与y轴交于点C，若过点C且平行于x轴的直线与该抛物线有两个不同的交点，并设另一个交点为D，问：△QCD能否为正三角形？若能请求出二次函数的解析式；
（3） 
在（2）的条件下，又设抛物线与x轴的交点之一为A，则能使△ACD的面积等于1/4的抛物线有几条？并证明你的结论。 y
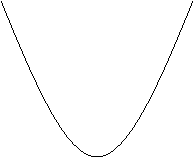
O N
x
M
C D
Q
（第2题图）
3．如图二次函数y=x2+（m-2）x-3m（m≥0）的图像与x轴交于A、B两点（A在B左边）
与y轴交于点C，顶点为D。S△ABC=6。
y
（1） 
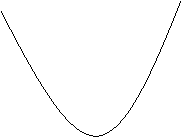求m的值；
（2） 求tg∠BDC的值；
（3） 
设直线CD交x轴于点E，那么
A
B
△BDE与△ABC是否相似？若是，
E
x
请证明；若不是，请说明理由。
B
D
（第3题图）
初中（2005）专题训练 共4页 第2页
图形构造类
4．如图，已知直角梯形ABCD中，∠A=∠B=90º，AD=3，BC=6，AB=m,m>3，且ED⊥CD，
交AB于点E。 A D
（1） 
求证：△DCE与△ADE相似；
（2） 
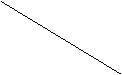当m为何值时，△DCE与△BCE相似？ E
B C
（第4题图）
5．正方形ABCD的边长是1，以A为圆心，AB长为半径作弧BD，动点M在弧BD上滑
动。过点M作弧BD的切线交DC、BC于点E、F，连接AF、AE交BD于点P、Q。
（1） 求∠EAF的度数；
（2） 
|
成一个直角三角形？若能，请
证明；若不能，请说明理由。 F
B A
（第5题图）
图形运动类
【说明：此类仅设两个大题，若要做详细练习，请参见“初中数学专题训练—图形运动”】
6．如图，在梯形ABCD中，E为AB上一点，DC=13，AD=BC=10，tanA=3/4。
（1） 求AB的长；
（2） 当点E离开点B距离为多少时， D C
以A、E、D为顶点的三角形与
以B、C、E为顶点的三角形相
似？
（3） 
如果P是边AB上的一点，且△ A
E
B
ADP与△DPC相似，求AP的长。 （第6题图）
7．如图，已知直角梯形ABCD中，AD∥BC，∠B=90º，AB=6，AD=8，BC=12，AB为
⊙O的直径，动点P从点A开始，沿AD边向点D以每秒1的速度运动，动点Q从点
C开始，沿CB边向点B以每秒3的速度运动，P、Q分别从A、C同时出发，当其中
一点到达端点时，另一点也随之停止运动。 A P
（1） 
当运动时间t为何值时，四边形
D
PQCD不是梯形？
（2） 当直线PQ与⊙O相切时，求：四
边形PQCD的面积。
B Q C
（第7题图）
初中（2005）专题训练 共4页 第4页