初三数学总复习（四）

初三数学总复习（四）

一、填空题（36分）

1．实数P在数轴上的位置如图，则　　　　　　　　　　　　　　　　＋　　　　　　＝　　

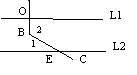
2．如图，直线l₁∥l₂，AB⊥l₁，垂足为O，BC与l₂相交于E，

若∠2＝48⁰，则∠1＝　　　

3．某数的平方为64，这个数的立方根为　　　　　　

4．小明的身高为1.6m，影长为2m同时古塔的影长为18m，则古塔的高为　　　　

5．不等式2x－1＜7的正整数解为　　　　　

6．如图：∠1＋∠2＋∠3＋∠4＝　　　　　　

7．用换元法解方程：x²＋　　＋2（　x＋　）－1＝　　　　

8．如图，AB是⊙O的直径，E为垂足，弦CD⊥AB于E，AB＝10，

CD＝8，则BE＝　　　　　

9．计算：　　sin45⁰－　cos60⁰＋tan30⁰＝　　　　　

10．已知关于x的不等式组　　　　　　　无解，则a的取值范围是　　　　　

11．函数y＝－kx（k≠0）与y＝－　的图象交于　A、B两点，过点A

作AC垂直于y轴垂足为C，则△BOC的面积为　　　　

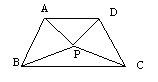
12．如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD则

∠PBC＝　　　　　

二、选择题（24分）

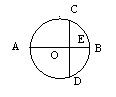
13．如图，在⊙O中，AB为直径，CD为弦，AE＝6，BE＝2，则CD＝（　　）

　A．4　　　　B．2　　　　C．　　　　D．4

14．如图，梯形ABCD，AD∥BC，∠B＝45⁰，∠C＝120⁰，

AB＝8，则CD的长是（　　）

　A．　　　　　B．4　　　　C．　　　　D．4

15．下列函数，图象一定经过原点的是（　　）

　A．y＝3x－2　　　　　　B．y＝

　B．y＝x²－3x＋1　　　　　　 D．y＝－　　x

16．如图，四边形ABCD内接于⊙O，则∠BOD＝（　　）

　A．150⁰　　 　　B．120⁰　　　　　C．170⁰　　　　　D．160⁰

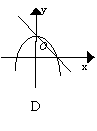
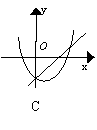
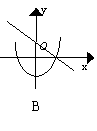
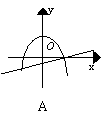17．下列各图中，是同一坐标系内二次函数y＝ax²＋（a＋c）x＋c与一交函数y＝ax＋c的大致图象是（　　）

18．下列各式计算正确的是（　　）

　A．a²·a⁵＝a¹⁰　　B．（a³）²＝a⁶　　C．（x－y）²＝x²－y²　　　D．a⁶－a⁴＝a²

19．下列命题中，①－4的平方根是－2；②近似数3.14有三个有效数字；③单项式3xy²与　　3x²y是同类项；④正方形是轴对称图形，又是中心对称图形，其中真命题的个数为（　　）

　A．1个　　　　　　 B．2个　　　　　C．3个　　　　D．4个

20．已知α²+α－1＝0，β²＋β－1＝0，且α≠β，则αβ＋α＋β的值为（　　）

　A．2　　　　　B．－2　　　　　C．－1　　　　　D．0

三、（每题5分，共15分）

21．已知Rt△ABC中斜边AB为9，直角边AC、BC是关于x的方程：x²＋（1－2m）x＋4（m－1）＝0的两根，求m。

　　

22．计算：

23．已知点I是△ABC的内心，射线AI交△ABC的外接圆于D，交BC于E。

求证：ID＝BD

四、（本题5分）

24．已知线段AB，求作线段AB的五等分点。（写作法，保留作图痕迹，写出结论）

五、（每题6分，共12分）

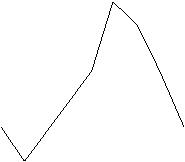
25．下图表示邵阳市2004年5月份某一天的气温随时间变化的情况，请观察此图回答下列问题：

（1）这天的最高气温是　　　　　度；

（2）这天共有　　　　个小时的气温在31度以上；

（3）这天在　　　　　　（时间）范围内温度在上升；

（4）请你预测一下，次日凌晨1点的气温大约是

多少度？答：　　　　　

26．如图，已知△ABC，∠ACB＝90⁰，AC＝BC，点E、F在AB上，∠ECF＝45⁰，（1）求证：　△ACF∽△BEC；（2）设△ABC的面积为S，求证：AF·BE＝2S

七、（本题8分）

27．已知一次函数y＝kx＋2的图像经过第一、二、三象限，且与x、y轴分别交于A、B两点，O是原点，若△AOB的面积为2，

（1）求一次函数的解析式；

（2）设点P（m，n）（其中n≥0）是一次函数y＝kx＋2图像上的点，过点P向以原点O为圆心，1为半径的⊙O引切线PC、PD，切点分别为C、D。当－2≤m≤0时，求四边形PCOD的面积S的取值范围

。
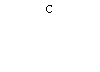