初三学业考试模拟测试数学试卷
（时间100分钟，满分120分）
| 题号 | 一 | 二 | 三 | 四 | 总分 | |||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | ||||||||||
一、填空题（本大题共14小题，每题3分，满分42分）
1、若一个数的平方根是
，则这个数是
。
2、当
=
时，分式
的值为0。
3、函数
的自变量的取值范围是
。
4、分解因式：
=
。
5、若
。
6、方程
的解是
。
7、已知二次函数
的图象向下平移3个单位后所得函数的解析式是
。
8、样本8、11、9、10、12的方差是 。
9、两个相似三角形的面积比为1∶9，则它们的周长比为 。
10、在△ABC中，BE是它的一条中线，G是△ABC的重心，若BE=3，则EG= 。
11、已知菱形的两条对角线长分别为8cm、10cm，则它的边长为 cm。
12、高为2m，坡度为30°的坡长为 m。
13、正五边形绕着它的中心至少旋转
度，能与它本
身重合。
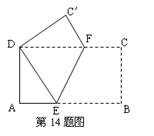
14、如图，在矩形
中，
将矩形折叠，使点B与点D重合，
落在
处，若
，则折痕
的长为
。
二、选择题（本大题共4小题，每题3分，满分12分）
（每题列出的四个答案中，只有一个正确的，把正确答案的代号填入括号内）
15、下列各数中，是无理数的是……………………………………………………（ ）
（A）3.14； （B）
；
（C）0； （D）
．
16、反比例函数
的图象经过点……………………………………………（
）
（A）（2，3）； （B）（1，6）；
（C）（9，
）； （D）（-2，-3）．
17、下列图形中，既是中心对称图形，又是轴对称图形的是……………………（ ）
（A）线段； （B）等腰三角形；
（C）平行四边形； （D）等腰梯形．
18、下列命题中，正确的是…………………………………………………………（ ）
（A）三点确定一个圆；
（B）平分弦的直径必垂直于这条弦；
（C）已知两圆的半径分别为
，圆心距为
，如果两圆外离，则
；
（D）圆心角相等，它们所对的弧也相等．
三、（本大题共3题，每题8分，满分24分）
19、解方程：
20、如图，在梯形中，
∥
，∠
=90°，
，
⑴ 求
的长；
⑵ 若∠
的平分线交于点
，连结
，求∠
的正切值。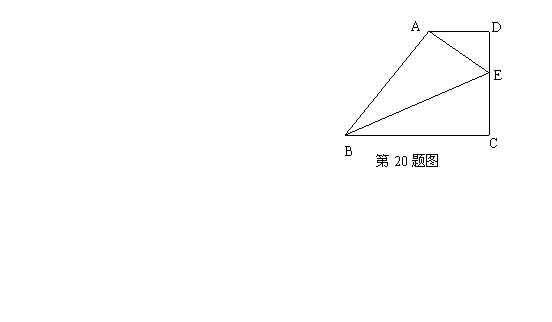
21、某电台“市民热线”抽查了某一周内接到热线电话，并进行分类统计，得到的统计信息如下表：
| 电话类型 | 房产城建 | 道路交通 | 环境保护 | 子女学习 | 其他方面 | 合计 |
| 电话次数 | 150 | 120 | ||||
| 占比例 | 25% | 20% |
| 25% | 100% |
根据上表所给的信息，回答下列问题：
（1）这一周“市民热线”接到的电话总数是 ；
（2）这一周“市民热线”接到关于子女学习方面的电话占本周总电话数的
（填写百分比）；
（3）据此估计“市民热线”一个月（按4.5周计算）接到的总电话数是 ；
（4）若将上表表示成扇形图，请你计算出有关环境保护方面电话的圆心角度数。
四、（本大题共4题，第22、23、24题每题10分，第25题12分，满分42分）
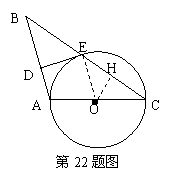
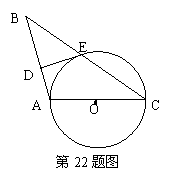22、如图，在等腰三角形ABC中，AB=AC，以AC为直径作圆O，与BC交于点E，过点E作ED⊥AB，垂足为点D，
(1) 求证：DE为⊙O的切线；
(2) 过O点作EC的垂线，垂足为H，
求证：
23、汽车产业的发展，有效促进我国现代化的建设，某汽车销售公司2004年共盈利1500万元，该公司预计2006年盈利2160万元，且计划从2004年到2006年，每年盈利的年增长率相同，问2005年该公司预计盈利为多少万元？
24、已知，关于的二次方程
的两个实数根为
.
（1）若方程的一个根是
，求
的值；
（2）若
，试求出
与的函数关系式以及的取值范围。
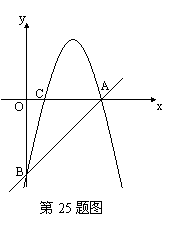
25、如图，一次函数
分别交轴、轴于
、
两点，二次函数
的图象经过
两点.
（1）求二次函数的解析式；
（2）设
是线段
上异于的两个动点，
。
①
若点
的横坐标为
，写出的坐标（用t的代数式表示）；
② 抛物线上是否存在点F，使点F与点D关于x轴对称，如果存在，请求出△AEF的面积；如果不存在，请说明理由。
 |
金山区2005年初三学业考试模拟测试数学答案
一、填空题（本大题14小题，每小题3分，满分42分）
1、4；2、
；3、
；4、
；5、5；6、
；7、
；8、2；9、
；10、1；11、
；12、4；13、72；14、4。
二、选择题（本大题共4小题，每题3分，满分12分）
15、D；16、C；17、A；18、C。
三、（本大题共3小题，每题8分，满分24分）
19、解：设：
， 原方程化为：
……………1分
，解得
，………………….2分
当
，解得
…………………………2分
当
，解得
………………………..2分
经检验，原方程的解为：，………………………….1分
20、（1）过点A作AF^BC垂足为F,由题意得FC=AD=2，AF=CD，………..1分
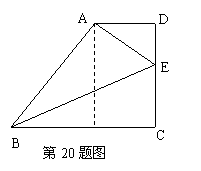∵BC=5，∴BF=3，………………………..1分
在Rt△AFB中解得AF=4, ∴CD=4…………………1分
（2）设EC=,由AB=BC，∠ABE=∠CBE，BE=BE，
得△ABE≌△CBE，
AE=EC=,∠AEB=∠CEB…………………….2分
|
，在Rt△ADE中，
，得
…………………..1分
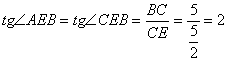…………..2分
21、（1）600………………2分，（2）10%................................2分，
（3）2700…………….2分，（4）72°…………………...2分.
四、（本大题共4题，第22、23、24题每题10分，第25题12分，满分42分）
22、证明：（1）连结OE，∵AB=AC，∴
......................1分
∵OC=OE，∴
……………..1分
∴
，∴ ∥
……..1分
∵
，∴
………..1分
∵ 是圆
的半径，
∴ 
为⊙的切线…………………….1分
（2）∵
，∴
.......1分
∵，
∴
∽
………………2分，∴
……………………………1分
∵
，∴…………………………………………….1分
23、解：设每年盈利的年增长率为………………………………1分
由题意得：
………………………….3分
解方程： 
，得
（负值舍取）…………..3分
…………………….2分
答：2005年该公司预计盈利1800万元。…………………………1分
24、解：（1）把代入得
………………………………1分
解得：
……..1分， ∵方程是二次方程，∴
，∴
...........1分
（2）
、
是方程的两个实数根，
…………………………….1分
=
…………..3分
∵方程有两个实数根，∴
，
...............2分
∴的取值范围是：
……………………………………………..1分
25、（1）∵一次函数
分别交轴、轴于
、两点，∴
…1分
∵在二次函数的图象上，∴解得
，
∴二次函数的解析式是：
……………….…2分
（2）①
或
.......................3分
② 存在. ∵抛物线上一点F与点D关于x轴对称，∴
，即
，解得
，∵不与重合，∴
，
∴存在点
与点D关于x轴对称。…………………………2分
当
时，
...........2分
当
时，
……………………2分
