初三教学情况调研测试数学试题

初三教学情况调研测试数学试题

题　号	一	二	三	四	五	六	合　计
得　分

　　　注意事项：1.全卷满分120分，考试时间120分钟，共6页，30道题．

　　　　　　　　2.考生在答题过程中，可以使用CZ1206型函数计算器。

一、填空题：（每小题2分，共20分）

1、－3的相反数是　　　　；－2的绝对值是　　　　 ；

2、方程²＝2的解是　　　　　　　 ；因式分解：³－＝　　　　　 ．

3、函数y＝的自变量的取值范围是　　　　 ．

4、抛物线＝－(＋2)²－3的对称轴为直线________；顶点坐标为____________.

5、写出一条经过第一、二、四象限，且过点(，)的直线解析式　　　　　   .

6、已知，则=_______.

7、一顶简易的圆锥形帐篷，帐篷收起来时伞面的长度有4米，撑开后帐篷高2米，则帐篷撑好后的底面直径是　　　　 米.

8、在Rt△ABC中，∠C＝90°，AC＝6，BC＝ 8，则其外接圆的半径为　　　　  .

9、圆心在轴上的两圆相交于A、B两点，已知A点的坐标为（－3，2），则B点的坐标是　　　　  .

10、用长4cm，宽3cm的邮票300枚不重不漏摆成一个正方形，这个正方形的边长等于______cm.

二、选择题：(每小题2分，共20分.在每小题给出的四个选项中，只有一个是正确的)

11、元月份某一天，北京市的最低气温为－6⁰C，常州市的最低气温为2⁰C，那么这一天常州市的气温比北京市的最低气温高 　　　　　　　　　　　　　　　　　　　　　　　　　　　【　　 】

　　(A)6⁰C　　　　　　 (B)4⁰C　　 　　　　(C)－8⁰C　　 　　　(D)8⁰C　

12、以下五家银行行标中，既是中心对称图形又是轴对称图形的有　　　　　　　　　　　 【　　 】

　 　 　　　　 

　　　 (A)1个　　　　　　　　　 (B)2个　　　　　　　　　 (C)3个　　　　　　　　　 (D)4个

13、用一个平面去截圆锥，截面图形不可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　【　　 】

14、在Rt△ABC的直角边AC边上有一动点P（点P与点A、C不重合），过点P作直线截△ABC，使截得的三角形与△ABC相似，满足条件的直线最多有　　　　　　　　　　　　　　　　　 【　　 】

　　(A)1条　　　 　　　(B)2条　　　 　　　(C)3条　　　　　　 (D)4条

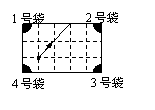15、如图是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入的球袋是　　　　　　　　　　【　　 】

　　(A)1 号袋　　 　　 (B)2 号袋　　　　　 

　　(C)3 号袋　　 　　 (D)4 号袋

16、一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为　　　　　　　　　　　　　　　　　　　　　　　　　 【　　 】

　　　 (A)6个　　　　　　　　　　　(B)8个　　　　　　　　　　　(C)12个　　　　　　　　　　(D)17个

17、生物学指出：生态系统中，每输入一个营养级的能量，大约只有10%的能量能够流动到下一个营养级，在H₁→H₂→H₃→H₄→H₅→H₆这条生物链中（H_n表示第n个营养级，n=1，2，……，6），要使H₆获得10千焦的能量，那么需要H₁提供的能量约为 　 【　　 】

　　（A）10⁴千焦　　　 （B）10⁵千焦　　　 （C）10⁶千焦　　　 （D）10⁷千焦

18、在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中，54.5～57.5这一组的频率是0.12，那么，估计总体数据落在54.5～57.5之间的约有　　　　　　　【　　 】

　　(A)6个　　　　　　 (B)12个　　 　　　 (C)60个　　　　　　(D)120个

19、若不等式组的解集是＞3，则m的取值范围是　　　　　　 【　　 】

　　(A)m>3　　  　　　　　 (B)m≥3　　　 　　(C)m≤3　　　　 　(D)m<3

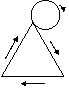20、如图，一个等边三角形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了　　　　　　　  【　　 】

　　　 (A)4圈　　　　　　　　　(B)3圈　　　 　　　　　

　　　 (C)5圈　　　　　　　　(D)3.5圈

三、解答题：（每小题5分，共10分）

21、计算：　　22、解方程：

四、（23题8分，24题4分，共12分）

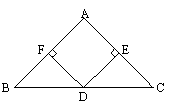
23、已知：如图，D是△ABC的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE.　求证：(1)△ABC是等腰三角形；

　　　　  (2)当∠A＝90°时，试判断四边形AFDE是怎样的四边形，证明你的结论.

24、在如图的12×24的方格纸中（每个小方格的边长都是1个单位）有一△ABC．现先把△ABC分别向右、向上平移8个单位和3个单位得到△A₁B₁C₁；再以点O为旋转中心把△A₁B₁C₁按顺时针方向旋转90º得到△A₂B₂C₂，请在所给的方格纸中作出△A₁B₁C₁和△A₂B₂C₂．

五、（25题10分，26题8分，27题10分，共28分）

25、一辆汽车要将一批10㎝厚的木板运往某建筑工地，进入工地到目的地前，遇有一段软地．聪明的司机协助搬运工将部分木板卸下铺在软地上，汽车顺利通过了．

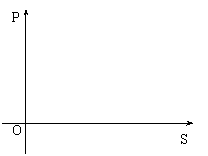⑴ 请你写出其中的道理：　　　　　　　　　　　　　　　　　　 ．如果卸下部分木板后汽车对地面的压力为3000N，若设铺在软地上木板的面积为S㎡，汽车对地面产生的压强为P（N/㎡），那么P与S的函数关系式是　　　　　　 ．

　　　 　 请在直角坐标系中，作出相应的函数图象．

⑵ 若铺在软地上的木板面积是30㎡，则汽车对地面的压强是　　　　　　 N/㎡．

⑶ 如果只要汽车对地面产生的压强不超过600N/㎡，汽车就能顺利通过，则铺在软地上的木板面积最少要　　　　　　 ㎡．　　

26、将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上.抽取一张，作为十位上的数字（不放回），再抽取一张作为个位上的数字.

⑴ 能组成那些两位数.

⑵ 这个两位数恰好是“32”的概率为多少.

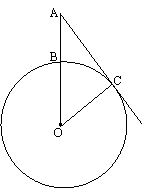27、如图，已知⊙O的半径为8cm，点A是半径OB延长线上一点，射线AC切⊙O于点C，弧BC的长为πcm，求线段AB的长（精确到0.01cm）.

六、（28题10分，29题8分，30题12分，共30分）

28、某班为了从甲、乙两位同学中选出班长，进行了一次演讲答辩与民主测评，A、B、C、D、E五位老师作为评委，对“演讲答辩”情况进行评价，全班50位同学参与了民主测评。结果如下表所示：

规定：演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定；

　　　民主测评得分＝“好”票数×2分＋“较好”票数×1分＋“一般”票数×0分

综合得分＝演讲答辩得分×(1－a)＋民主测评得分×（0.5≤≤0.8）

⑴ 当＝0.6时，甲的综合得分是多少？

⑵ 在什么范围内，甲的综合得分高？在什么范围内，乙的综合得分高？

29. 某学校9年级的一场篮球比赛中，队员甲正在投篮，已知球出手时离地面20/9m，与篮圈中心的水平距离为7m。当球出手后水平距离为4m时达到最大高度4m。设篮球运行轨迹为抛物线，篮圈距地面为3m.

⑴建立适当的平面直角坐标系，试判断此球能否投中。

⑵此时若对方队员乙在甲面前1m处跳起盖帽拦截。已知乙的最大摸高为3.1m，那么他拦截能否获得成功？

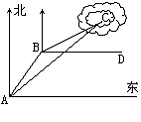
30. 一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？

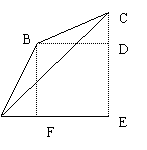
31. 如图，已知△ABC中，∠C＝900，∠B＝600，AC＝4，等边△DEF的一边在直角边AC上移动，当点E与点C重合时，点D恰好落在AB边上。

⑴求等边△DEF的边长。

⑵请你探索，在移动过程中，线段CE与图中的哪条线段始终保持相等，并说明理由。

⑶若设线段CE为x，在移动过程中，等边△DEF与Rt△ABC两图形重叠部分的面积为y。请你写出y与x的函数关系式。并写出自变量x的取值范围。

这是原试卷的最后一题：

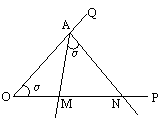
 如图：已知A为∠POQ的边OQ上一点，以A为顶点的∠MAN的两边分别交射线OP于M、N两点，且∠MAN＝∠POQ＝α（α为锐角），当∠MAN以点A为旋转中心，AM边从与AO重合的位置开始，按逆时针方向旋转（∠MAN保持不变）时，M、N两点在射线OP上同时以不同的速度向右平行移动，设OM＝x，ON＝y（y＞x≥0），△AOM的面积为s，若cosα=,OA=2。　

（1）　　当∠MAN旋转30⁰（即∠OAM＝30⁰）时，求点N移动的距离；　

（2）　　求证：

（3）求y与x之间的函数关系式及自变量x的取值范围；

（3）　　　 试写出s随x变化的函数关系式，并确定s的取值范围。

数学参考答案

一、（2′×10＝20′）

1、3；2－.　2、x1=0或x2=2.  3、x(x+1)(x-1).　4、x≤.　5、x=-2;(-2,-3).

5.y=-x+2等.　6、.　7、4.　8、5.　9、(-3,-2).  10、2.

二、（2′×10＝20′）

D　B  D　C　B  C　C　D  C　A

三、(5′×2＝10′)

21、解：原式＝1＋9＋3－9×―――1个对1分

＝10　―――5′

22、解：6－3（x+1）=x²-1 ------1′

　　　　x²+3x-4=0　 -----------2′

　　　  ∴x1=-4,x2=1　---------4′

经检验：x1=-4是原方程的根　　―――5′

四、（8′＋4′＝12′）

23、解：（1）∵BD＝CD，BF＝CE　　

∴Rt△BDF≌Rt△CDE　-----------2′

∴∠B=∠C　 ---------------3′

△ABC是等腰三角形　　――4′

　　　　（2）∵∠A＝90⁰，DE⊥AC，DF⊥AB

∴四边形AFDE是矩形　　――――2′

又∵Rt△BDF≌Rt△CDE　

∴DF＝DE　　―――――――――3′

∴四边形AFDE是正方形　　――――4′

24、画对1个2′

五、（8′＋6′＋10′＝24′）

25、压强原理　－1′;P＝　－2′；图像　－1′；100　－2′；5　－2′.

26、（1）树状图　――2′；两位数：12、13、21、23、31、32；　――2′

（2）P＝　――2′

27解：∵l==　---2′

∴n=50　 ------------3′

∴∠BOC=50⁰　---------4′

∵AC切O于C　　

∴OC⊥AC　　――――――6′

∴OA＝≈12.45 --------8′

∴AB=OA-OB=4.45(m)　 ---------10′

六、（10′＋8′＋6′＝24′）

28、解：设综合得分为T，演讲得分为T₁，民主测评得分为T₂

　　　（1）甲同学：T₁≈93.67, T₂=87　　―――1′

a=0.6时　T_甲≈90　―――――3′

（2）乙同学：T₁≈91.33, T₂=88

  T_乙＝91.33-3.33a  ------------------5′

又∵ T_甲=93.67-6.67a　--------------------6′

由T_甲> T_乙:a<0.7　----------------------8′

∴0.5≤a＜0.7时，甲的综合得分高　　―――9′

　0.7＜a≤0.8时，乙的综合得分高　　―――10′

29、解：（1）设y=a(x-4)²+4  ----1′

x=0时，y=

y=-　--------3′

y=-(x-4)²+4  ----4′

x=7时，y=---=3 

球能够投进　　　―――5′

　　　　（2）x＝1时，y=---=3<3.1

　　　　　 队员乙拦截成功　――――――6′　　 图像　2′

A

30　　　　　　　　　　 求出：BF＝5，AF＝5　　――2

　　　　　　　　　　　　设CD＝x

　　　　　　　　　　　  5+x=x+5 -------4′

　　　　　　　　　　　  x=5>4.8 ―――――――5′

不会有危险　―――――6′

七、（10′）

31、（1）边长为2　---3′

(2)CE=DG　---4′;证出：6′.

(3)y=-x²  ---9′; 0<x≤2. ---10′