初三升学模拟试题数学试卷
|
| 一 | 二 | 三 | 四 | 五 | 合计 | |||||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | |||||||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
| ||||
说明：全卷共120分，时间为90分钟。
一、选择题（每题3分，共15分）
1、下列运算正确的是 （ ）
A 
B 
C 
D 
2、若二次函数
的图像开口向下，则一次函数
的图像不经过（ ）
A 第一象限 B 第二象限 C 第三象限 D 第四象限
|
3、足球比赛的计分规则为：胜一场得3分，平一场得1分，负一场0分。一个队打14场负5场共得19分，那么这个队胜了 （ ）
A 3场 B 4场 C 5场 D 6场
4、如图1，在梯形ABCD中，EF是中位线，AD=6㎝，BC=10㎝，则四边形AEFD与四边形EFCB的面积之比 （ ）
A 3：4 B 4：5 C 7：9 D 5：9
5、已知，如图2，在△ABC中，AD⊥BC于D ，下列条件：①∠B+∠DAC=90°
②∠B=∠DAC ③
④
其中一定能够判定△ABC是直角三角形的共有 （ ）
A 3个 B 2个 C 1个 D 0个
|
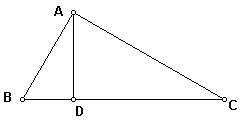
图1 图2
二、填空题（每题4分，共20分）
6、化简：
。
7、函数
中，自变量
的取值范围是
。
8、等边三角形ABC的边长是4，以AB边所在的直线为轴，AB边的中点为
原点，建立直角坐标系，则顶点C的坐标为 。
9、如果一个正方形的对角线长为4㎝，则此正方形的面积为 。
10、若扇形的面积为3
㎝
，弧长为2㎝，则其圆心角为 度。
三、解答下列各题（每题6分，共30分）
11、计算：
12、先化简，再求值：
，其中
13、解下列不等式组（要求利用数轴求出解集）
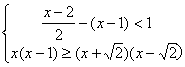
14、如图3，A、B、C三点表示三个村庄，为了解决村民子女就近入学的问题，计划
新建一所小学，要使学校到三个村庄的距离相等，请你在图中用尺规确定学校的位置。
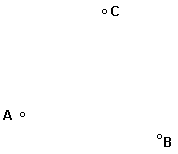
图3
15、解方程：
四、（每小题7分，共28分）
16、为了参加北京市申办2008年奥运会的活动，某班学生争取到制作240面彩
旗的任务，有10名学生因另有安排没能参加制作，因此这班的其余学生人均比
原计划多做4面彩旗才能完成任务，问这个班有多少名学生？
17、已知
，
是方程
的两个实根且满足
。求
的值。
18、已知一次函数
与反比例函数
的图像交于A、B两点，A点的纵
坐标与B点的横坐标分别是二次函数
的顶点的横坐标与纵坐标，求一
次函数的解析式。
| ||||
|
19、如图，⊙O是△ABC的外接圆，∠ACB的平分线CE交AB于点D，交⊙O于点
E，⊙O的切线EF交CB的延长线于点F。
求证：
|
五、（每小题9分，共27分）
20、公园里有甲、乙两群游客正在做团体游戏，两群游客的年龄如下（单位：岁）：
甲群：13，13，14，15，15，15，15，16，17，17
乙群：3，4，4，5，5，6，6，6，54，57
解答下列各题（直接填在横线上）：
（1）甲群游客的平均年龄是 岁，中位数是 岁，众数是 岁，其中能
较好反映甲群游客年龄特征的是 。
（2）乙群游客的平均年龄是 岁，中位数是 岁，众数是 岁，其中能
较好反映乙群游客年龄特征的是 。
（3）从甲群游客中抽出5位不同年龄的游客，他们的年龄方差为 。
21、比较下面的两个几何图形的异同。
（正三角形） （正六边形）
（1）两个几何图形的相同点有：
①
②
③
④
⑤
（2）它们的不同点有：
①
②
③
④
22、已知：如图，△ABC内接于⊙O，D是优弧AB上一个动点（不与A、B重合），DC交AB于E，DB的延长线交过C点的切线于点F，且AB∥CF，BC=4，∠ACB=120°。
（1）求AE+BE。
（2）设CE=，AE
BE
，求
与之间的函数关系式（不必写出自变量的取值范围）。
