初三数学第二次月考试卷
一、填空题：（每空2分，计34分）
1、下列方程：（1）
（2）
（3）
（4）
（5）
其中是一元二次方程的有（
）；是分式方程的有（
）（填序号）
2、在实数范围内分解因式：
（
）
3、解方程
时，设y=（ ）原方程化为（
）
4、若一元二次方程
没有实数根，则k的最小整数值是（
）
5、列车在途中因故停车5分钟，而后提速运行，每小时比原来多行5千米，前进30千米后就把耽误的时间追回来，问列车原来运行的速度是多少？若设列车原来运行的速度为x千米/时，则列出的方程为（ ）
6、经过已知点A、B可以作（ ）个圆，这些圆的圆心轨迹是（ ）
7、已知，
， sinA+cosB=
，则tanA=(
)
8、三角形（ ）叫三角形的外心，三角形的外心具有的性质是（ ）
9、△ABC中，∠C=90度 BC=3cm，AC=4cm，D为斜边AB的中点，以B为圆心，BC为半径作圆，那么点A、D、C与的⊙B位置关系是：点A在⊙B的（ ）,点D在⊙B的( ),点C在( )
10、如图，AB为⊙O的弦，C为AB上一点，
且∠OCA=∠AOC=72度，OA=2 那么
∠B=（ ）BC=（ ）
二、选择题：（每空3分，计30分）
11、下列命题是真命题的是（ ） A C B
（A）平分弦的直径垂直于弦 （B）垂直于弦的直线必过圆心
（C）三点可以确定一个圆 （D）直径是圆的弦
12、Rt△ABC中，斜边的中线长为7，则△ABC外接圆的直径是（ ）
（A）14 （B）7 （C）
（D）不能确定
13、在⊙O中弦AB的长为10cm，点O到AB的距离为
cm，则∠AOB的度数为（ ）
（A）150度 （B）120度 （C）90度 （D）60度
14、在半径为R的圆中，垂直平分半径的弦长为（ ）
（A）
（B）
（C）
（D）
15、已知⊙O的直径为26 cm，在圆心O的两侧有两条平行弦AB、CD，已知AB=24 cm，CD= 10cm 则AB、CD的距离为（ ）
（A）7 cm 或1cm （B）7cm或17 cm （C）7cm （D）17cm
16、下列说法中：①a=b的反面是a>b ②A>60度的反面是A<60度 ③点P在直线a上的反面是点P在直线a 外 ④点A在⊙O上的反面是点A在⊙O外， 其中不正确的有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
17、二次三项式：①
②
③
④
在实数范围内不能分解的有：（
）
（A）①④ （B）②③ （C）①③ （D）②④
18、若关于x的方程
有增根，m值为（
）
（A）4 （B）2 （C）±4 （D）±2
19、由方程组：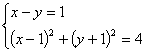
消去y化简后得到的方程是（
）
（A）
（B）
（C）
（D）
20、某化肥厂一月份生产尿素5000吨，后来改进操作技术，使第一季度共生产化肥17500吨，求二、三月份平均每月增长的百分率x，所得的方程为（ ）
（A）
（B）
（C）
（D）
初三数学第二次月考试卷
一、1、（ ）；（ ） 2、（ ） 3、（ ）；（ ）
4、（ ） 5、（ ） 6、（ ）；（ ） 7、（ ）
8、（ ）；（ ）9、（ ）；（ ）；（ ）
10、（ ）；（ ）
二、1、 2、 3、 4、 5、
6、 7、 8、 9、 10、
三、解答题：（21题10分，22、23各题6分，24、25各题7分，总计36分）
21、解下列方程或方程组：
（1）
（2）
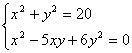
22、已知在⊙O中，半径R=2，弦AB=
AB=
求∠BAC的的度数（自己先画图，再写出计算过程）
23、已知如图，AB是⊙O的直径，CD是弦，AE⊥CD垂足为E，BF⊥CD垂足为F，求证：CE=DF
E
A C
D
F
B
24、某商场销售一批名牌产品，平均每天可以售出20件，每件盈利40元，为扩大销售，增加盈利，减少库存，商场决定采取适当的降价措施，经调查发现，如果每件产品每降价1元，平均每天可多出售2件，若商场平均每天要盈利1200元，问每件产品应降价多少元？
25、有两条公路OM、ON相交成30度角，沿公路OM方向有一所中学A，AO=160米，当拖拉机沿ON方向行驶时，其噪音将对周围100米范围产生影响，已知拖拉机每小时行18千米，那么拖拉机沿ON方向行驶时，是否会给中学带来影响？若不受影响，请说明理由，若受影响，请计算影响的时间。
N
O A M
26、附加题：
经调查研究，目前我国国民总产值每增加一个百分点，就可增加90万人的就业机会，若今后两年内要增加1500万人的就业机会，那么国民总产值在今后两年内平均每年增长率是多少？(
)
初三数学第二次月考答案及评分标准
一、填空题：（每空2分，共计34分）
1．①②； ④ 2、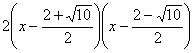
3、
；
4、2 5、
6、无数； 线段AB的垂直平分线 7、
8、外接圆的圆心； 到三角形三个顶点距离相等 9、外部， 内部； ⊙B上 10、
； 
二、选择题：（每题3分，共计30分）
DADCD CBDAD
三、解答题：（21题10分，22、23各题6分，24、25各题7分，总计36分）
21、（1）解： 去分母，得 
（1分）
整理， 得
（2分）
解， 得
，
（4分）
经检验：，都是原方程的解
（5分）
（2）、解： 由②得 
（1分）
原方程组可化为：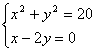
和 
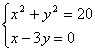（3分）
解，得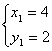 
; 
; 
; 
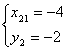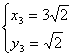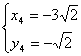; （5分）
22、解：情况（1） 如图（1）作
，
则
（2分）
又
半径
（3分）
（4分）
情况（2） 如图（2） 当AB、AC在圆心O同侧时，
(6分)
23、证明：作
于H 由垂径定理，得CH=DH
（2分）
又
AB为⊙O直径 
（4分）
即 CE=DF
（6分）
24、解：设每件产品降价
元， 依题意得 
（3分）
整理，得 
即
解，得 
（5分）
要尽快减少库存， 
不合题意（舍去） 
答：每件产品就降价20元。 （7分）
25、解：过点A作
于H
（1分）
在Rt△AOH中，OH=160米，∠AOH=
∴ 
（3分）
∴会给中学带来影响 （4分）
设ON上有B、C两点满足AB=AC=10m
在Rt△ABH中，
∴BC=2BH=120（m） （6分）
又∵速度 18千米/时=5米/秒
∴ 时间 
（秒）
（7分）
26、附加题：设平均每年增长率为x 
则： 
（4分）
即 
∴
负值舍去
∴
（6分）
答：平均每年增长率约为8% （7分）