初三数学第一学期期末复习试题卷

初三数学第一学期期末复习试题卷

考生须知：

1、本试卷分试题卷和答题卷两部分。满分120分，考试时间100分钟。

2、答题前，必须在答题卷密封区内填写试场号、座位号、班级、姓名。

3、所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应。

4、考试结束后，只需上交答题卷。

一、选择题（每题3分，共45分）

1、一名运动员百米跑的成绩为9.82秒，他的速度与下面比较接近的机动车是（　　　 ）

A、速度为40千米/时的拖拉机　　　　 B、速度为60千米/时的摩托车

C、速度为80千米/时的大卡车　　　　 D、速度为100千米/时的小轿车

2、一个居民小区的平面图如右图所示，其比例尺1：5000（单位：cm），则这个小区的围墙长为（　　 ）

A、200m　　　　　  B、400m

C、600m　　　　　  D、800m

3、为绿化环境，在山坡上植树，根据要求株距（相邻两树间的水平距离）应为3米，测得斜坡的坡角为21^ο，则相邻两树间的坡面距离应为　(　　　 )（精确到0.1米，参考数据。Sin21^ο≈0.36，cos21^ο≈0.93， tan21^ο≈0.38　cot21^ο≈2.61）

A、1.2米　　　　　 B、3.2米

C、2.8米　　　　　 D、3.5米

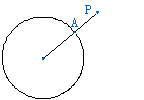
4、如图：将地球近似地看作一个半径为a的圆，在某一时刻“神舟五号”飞船P和地球表面最近距离是PA=b,则这时飞船p发出的电波到地球表面最远处要经过的路程长是（　 ）

A、2a+b　 　　　 B、　　　　  C、　　　　 D、

5、已知平行四边形一锐角的余弦值为，一组邻边的长分别为、2，则平行四边形的面积为（　　）

A　 　　　　　B　 　　　 C　　　　　　 D　　3

6、某公园中的儿童游乐场是两个相似三角形地块，相似比为2:3，面积的差为30m²，它们的面积和为（　　）

A、74 m²　　　　　　 B、76 m²　　　　　  C、78m²　　　　　  D、81m²

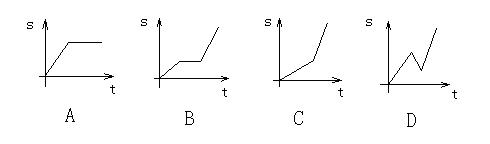
7、小明骑自行车上学，开始以正常速度匀速行驶，但行至途中自行车出了故障，只好停下来修车，车修好后。因怕耽误上课，他比修车前加快了骑车速度匀速行驶。下面是行驶路程 S（米）关于时间t（分）的函数图象。那么符合这个同学行驶情况的图象大致是（　　 ）

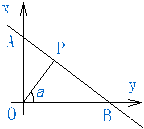8、如图：已知∠α的终边OP⊥AB,直线AB的表达式为

y=-χ+，则cosα=　(　　　　  )

A、　　　　B、　　　 C、　　　　D、

9、某公司员工分别住在A、B、C三个住宅区，A区有30人，B区有15人，C区有10人三个区在同一直线上，位置如图所示，该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小即使停靠点应该在（　　 ）

A、A区　　　　　　 B、 B区　　　　　　 C、 C区　　　　 D、A、B两区之间

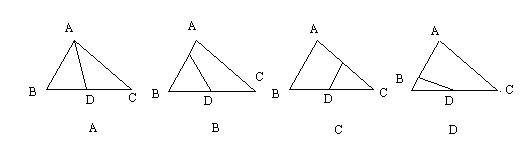
10、把三角形的纸片一刀剪成两片，使两片拼成一个平行四边形，下图中的哪一种剪法（D是BC的中点）是正确的（　　）

11、已知θ为锐角,且点（tanθ,cotθ）在第一象限的角平分线上，那么（cosθ－sinθ）²的值等于（　　）

A、0　　　　　　　 B、　　　　　  C、　　　　　　 D、

12、某化学反应2A+3B→2C，其中 A和C在反应中的质量关系如图，则当有15克 C生成时，消耗B的质量是（　　　）

A、5克　　B、7.5克　　C、10克　　D、12.5克

13、用一根长为20cm的铁丝折成一个扇形，当扇形的面积最大时，半径取何值。（　　）

A、3cm 　　　　B、10cm 　　　 C、5cm　　　D、2cm

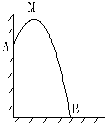
14、某幢建筑物，从10米高的窗口A用水管向外喷水，喷出的水流呈抛物线，（物线所在的平面与墙面垂直，如图）如果抛物线的最高点M离墙1米，离地面米，则水流落点B离墙的距离OB是（　　 ）

A、2米　　　　　  B、3米

C、4米　　　　　  D、5米

15、方程的根为、，设＜则（　　 ）

A、₁＜1＜₂　　　　 B、₁＜10＜₂　　

C、₁＜1000＜₂　　 D、₁＜2003＜₂

二、填空　（每题4分，共20分）

16、如图：一个小球由静止开始在一个斜坡上匀下滚动，通过仪器观察得到小球滚动的距离S（米）与时间t（秒）的数据如下：

时间t(秒)	1	2	3	4	……
距离 s（米）	2	8	18	32

那么s与t之间的函数关系式是_______________

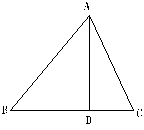
17、如图，已知△ABC中,AD是高,∠BAC=45°,BD=3，DC=2，则AD=______

18、有一抛物线经过点A（-1，0），B（m，0），C（1，n），旦m+n=-1，

mn= -12，那么此抛物线的解析式是_____________

19、观察下面一列数字的规律并填空：0，3，8，15，24……，

则它的第2002个数是______。

20、如图，已知边长为2的正三角形ABC沿直线滚动，

(1)当△ABC滚动一周到△A₁B₁C₁的位置，此时A点所运动的路程为______，约为______ ；（精确到0.1，π=3.14……）

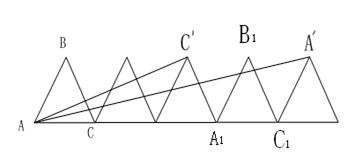(2)设△ABC滚动240°时，C点的位置为C^‘，△ABC滚动480°时，A点的位置为A^‘，请你利用三角函数中正切的两角和公式tan(α+β)=（tanα+tanβ）÷（1－tanα·tanβ）,求出∠CA C^‘+∠CA A^‘的度数为　　　　

 

三、解答题

21、（7分）计算：

22、（8分）解方程：

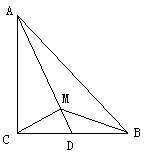
23、（8分） 如图，Rt△ABC中，∠ACB=90°，M是BC的中点，

CD⊥AM于点D，求证：AM·BD=BM·AB

24、（10分）已知关于的方程的两根a、b是Rt△ABC的两条直角边长（a≠b），且Rt△ABC的斜边长为13，求m的值。

25、（10分）已知命题：如果对一切实数，恒有＞0，（、为常数），

那么＜

（1）、证明这个命题。

（2）写出此命题的逆命题。

（3）判断此命题逆命题是否成立，若成立请证明，若不成立请举一反例说明。

26、（12分）如图，以△ABC的边AC为直径的半圆交AB于D，三边长a，b，c能使二次函数的顶点在轴上，且是方程的一个根。

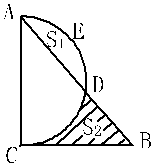（1）证明：∠ACB=90°；

（2）若设b=2，弓形面积S_弓形AED=S₁，阴影部分

面积为S₂，求（S₂－S₁）与的函数关系式；

（3）在（2）的条件下，当b为何值时，（S₂－S₁）最大？