数学中考试卷
一、精心选一选（本大题共10小题，每题3分，共30分. 在每题所给出的四个选项中，只有一项是符合题意的. 把所选项前的字母代号填在括号内. 相信你一定会选对！）
1、函数
中自变量x的取值范围是（ ）
A、
B、
C、
D、
2、某物体的三视图如下，那么该物体形状可能是（ ）
 |
A、长方体 B、圆锥体 C、立方体 D、圆柱体
3、下列图形中，既是轴对称，又是中心对称图形的是（ ）
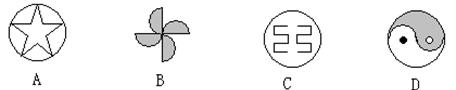
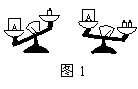4、如图1，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可表示为（ ）
 |  | ||
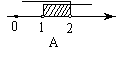
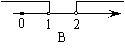
5、把分式方程
的两边同时乘以(x-2), 约去分母，得( )
A．1-(1-x)=1 B．1+(1-x)=1
C．1-(1-x)=x-2 D．1+(1-x)=x-2
6、在一副52张扑克牌中（没有大小王）任意抽取一张牌，抽出的这张牌是方块的机会是（ ）
A、
B、
C、
D、0
7．将函数
进行配方正确的结果应为（ ）
A 
B
C 
D
8、一个形式如圆锥的冰淇淋纸筒，其底面直径为
，母线长为
，围成这样的冰淇淋纸筒所需纸片的面积是
（ ）
A、 
B、 
C、 
D、 
9、某村的粮食总产量为a（a为常量）吨，设该村粮食的人均产量为y（吨），人口数为x，则y与x之间的函数图象应为图中的（ ）
 |  |  |  | ||||
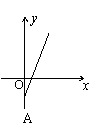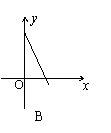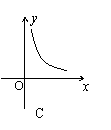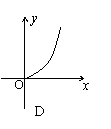10、在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁，每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存，已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例，为使选定的工厂仓库储存所有产品时总的运费最省，应选的工厂是（ ）
A、甲 B、乙 C、丙 D、丁
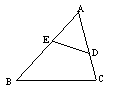二、细心填一填（本大题共有5小题，每空4分，共20分．）
11、分解因式：3x2－12y2= .
12．如图9，D、E分别是△ABC的边AC、AB上的点，请你添加一个条件，使△ADE与△ABC相似．你添加的条件是
．
13．如下图所示，摆第一个“小屋子”要5枚棋子，
摆第二个要11枚棋子，摆第三个要17枚棋子，则摆
第30个“小屋子”要 枚棋子
14、如图是2005年6月份的日历，如图中那样，用一个圈竖着圈住3个数．如果被圈的三个数的和为39，则这三个数中最大的一个为 ．
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 |
| 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
16
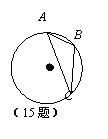15．如图，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30°，则⊙O的直径为__________cm.
三、认真答一答（本大题共10小题，满分100分. 只要你认真思考, 仔细运算, 一定会解答正确的!）
16、(本题满分8分)计算：解方程组：
17．(本题满分8分) （3）先将
化简，然后请自选一个你喜欢的x值，再求原式的值.
18．(本题满分8分) 在如图的方格纸中（每个小方格的边长都是1个单位）有一点O和△ABC.
（1）请以点O为位似中心，把△ABC缩小为原来的一半（不改变方向），得到△A′B′C′.
 |
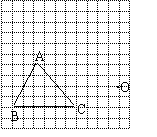（2）请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置.
19．(本题满分10分) 
（1）如图，在□ABCD中，对角线AC、BD相交于点O. 请找出图中的一对全等三角形，并给予证明.
20（本小题满分10分）
在某旅游景区上山的一条小路上，有一些断断续续的台阶.图11是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：
（1）两段台阶路有哪些相同点和不同点？
（2）哪段台阶路走起来更舒服？为什么？
（3）为方便游客行走，需要重新整修上山的小路.对于这两段台阶路，在台阶数不娈的情况下，请你提出合理的整修建议.
 |
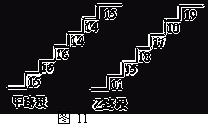21.（本题满分10分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克. 经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克.
（1）现该商场要保证每天盈利6000元，同时又要顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？
22．（本题满分10分）小明和小亮进行百米赛跑，小明比小亮跑得快，如果两人同时起跑，小明肯定赢，现在小明让小亮先跑若干米，两人的路程
（米）分别与小明追赶时间
（秒）的函数关系如图所示。
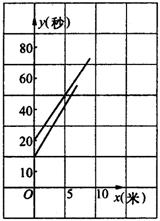⑴小明让小亮先跑了多少米？
⑵分别求出表示小明、小亮的路程与时间的函数关系式。
⑶谁将赢得这场比赛？请说明理由。
23．（12分）用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
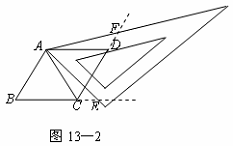
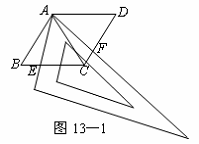（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.
24(本题满分12分)、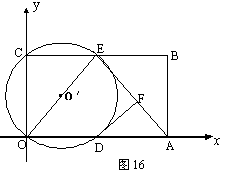
如图16，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交轴于D点，过点D作DF⊥AE于点F．
（1） (4分) 求OA、OC的长；
解：
（2） (4分) 求证：DF为⊙O′的切线；
证明：
（3） (4分) 小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．
解：
25(本题满分12分)、已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.
①当BC=1时，求矩形ABCD的周长；
②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由.