中考试题分类
《圆3》
三．解答题：
(成都): 24. （本小题满分8分）
如图9—1，一个圆球放置在V形架中.图9—2是它的平面示意图，CA和CB都是⊙O
的切线，切点分别是A，B.如果⊙O的半径为
cm，且AB=6cm，求∠ACB.
 |
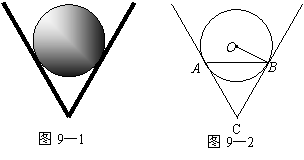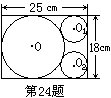
(锦州市) 24.某乡薄铁社厂的王师傅要在长为25cm，宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆.他先画出了如下的草图，但他在求小圆半径时遇到了困难，请你帮助王师傅计算出这两个小圆的半径.
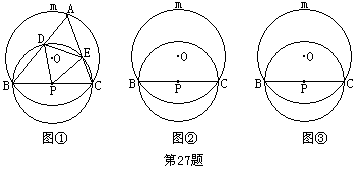
27.如图，⊙O与⊙P相交于B、C两点，BC是⊙P的直径，且把⊙O分成度数的比为1:2的两条弧，A是
上的动点(不与B、C重合)，连结AB、AC分别交⊙P于D、E两点.
(1)当△ABC是锐角三角形(图①)时，判断△PDE的形状，并证明你的结论；
(2)当△ABC是直角三角形、钝角三角形时，请你分别在图②、图③中画出相应的图形(不要求尺规作图)，并按图①标记字母；
(3)在你所画的图形中，(1)的结论是否成立？请就钝角的情况加以证明.
八、解答题(本题共14分)
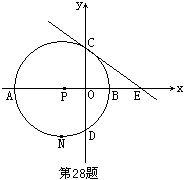
28.如图，点P是x轴上一点，以P为圆心的圆分别与x轴、y轴交于A、B、C、D四点，已知A(-3,0)、B(1,0)，过点C作⊙P的切线交x轴于点E.
(1)求直线CE的解析式；
(2)若点F是线段CE上一动点，点F的横坐标为m，问m在什么范围时，直线FB与⊙P相交？
(3)若直线FB与⊙P的另一个交点为N，当点N是
的中点时，求点F的坐标；
(4)在(3)的条件下，CN交x轴于点M，求CM·CN的值.
(泰州市) 12. 给出下列四个命题：如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；
(1) 若点A在直线y＝2x－3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；
(2) 半径为5的圆中，弦AB＝8，则圆周上到直线AB的距离为2的点共有四个；
(3)
若A（a，m）、B（a－1，n）（a>0）在反比例函数
的图象上，则m<n．
其中，正确命题的个数是
A．1个 B．2个 C．3个 D．4个
七、（本题12分）
28. 如图，B为线段AD上一点，△ABC和△BDE都是等边三角形，连结CE并延长交AD的延长线于F，△ABC的外接圆⊙O交CF于M.
⑴ 求证：BE是⊙O的切线；
⑵ 求证：AC2＝CM·CF；
⑶ 若CM＝
，MF＝
，求BD；
⑷ 若过点D作DG∥BE交EF于G，过G作
GH∥DE交DF于H，则易知△DGH是等边三角
形。设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3，试探究S1、S2、S3之间的等量关系，请直接写出其结论。
八、（本题12分）
29. 抛物线y＝ax2＋bx＋c (a<0)交x轴于A（－1，0）、B（3，0），交y轴于C，顶点为D，以BD为直径的⊙M恰好经过点C.
⑴ 求顶点D的坐标（用a的代数式表示）；
⑵ 求抛物线的解析式；
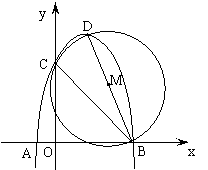⑶ 抛物线上是否存在点P，使△PBD为直角三角形？若存在，求出点P的坐标；若不存在，说明理由。
(吉林省) 五、解答题（第23题8分，第24题9分，共17分）
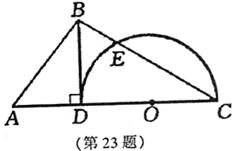
23．如图，在△ABC中，BD⊥AC于D，DC=2AD. 以DC为直径作半圆O，交BC于点E，
且BD=2BE=2.
（1）求半圆O的半径R；（4分）
|
(广东省)
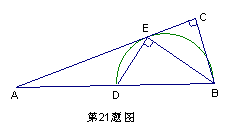
21. 如图，在Rt△ABC中，
,BE平分∠ABC交AC于点E，点D在AB上
.
（１）求证：AC是
的外接圆的切线；
（２）若
，求BC的长.
(深圳市)
21、直线y= -x+m与直线y=
x+2相交于y轴上的点C，与x轴分别交于点A、B。
（1）求A、B、C三点的坐标；（3分）
（2）经过上述A、B、C三点作⊙E，求∠ABC的度数，点E的坐标和⊙E的半径；（4分）
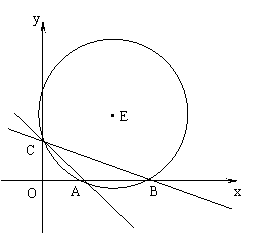（3）若点P是第一象限内的一动点，且点P与圆心E在直线AC的同一侧，直线PA、PC分别交⊙E于点M、N，设∠APC=θ，试求点M、N的距离（可用含θ的三角函数式表示）。（5分）
21、参考答案（1）（2，0），（2
，0），（0，2）
（2）30º；（
，）；2
（3）可自己先推证一个事实：
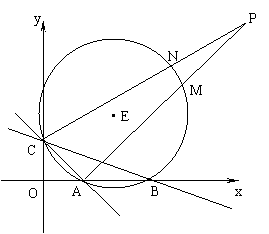如图所示：MN为⊙E中任一弦，它对的圆周角为∠B，AM为直径，则∠ANM为直角，则sinB=sinA=
即MN=AM·sinA （*）（其实就是正弦定理）
这是本题的解题的理论基础。
（I）当点P在⊙E外时，如图
连接AN，
则∠MAN=∠ANC-∠P=∠ABC-∠P
=30º-θ
由（*）得：MN=4sin(30º-θ)
（II）当P在⊙E内时
同理可得：MN=4sin(θ-30º)
其它情况研究方法相同。
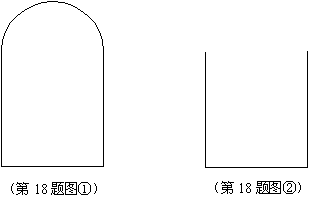
(佛山市) 18．图①为一个窗子的轮廓线，是由半圆和矩形相接而成，请你在图②中补作一个半圆，使它与图①完全相同（要求：用尺规作图，不写作法和证明，但保留作图痕迹）．
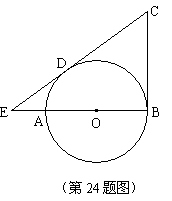
24．如图，AB是⊙O的直径，CD与⊙O切于D，CB⊥AB，延长CD、BA交于E。若EA=1，ED=2，求CD的长。
(福州市) 五、（满分10分）
25、已知：如图，AB是⊙O的一条弦，点C为
的中点，CD是⊙O的直径，过C点的直线
交AB所在直线于点E，交⊙O于点F。
（1）判定图中
与
的数量关系，并写出结论；
（2）将直线绕C点旋转（与CD不重合），在旋转过程中，E点、F点的位置也随之变化，请你在下面两个备用图中分别画出在不同位置时，使（1）的结论仍然成立的图形，标上相应字母，选其中一个图形给予证明。
(无锡市) 24.(本题满分6分)
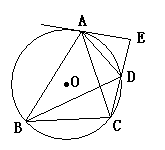
已知：如图，四边形ABCD内接于⊙O，过点A的切线与CD的延长线交于E，
且∠ADE＝∠BDC.
⑴求证：ΔABC为等腰三角形；
⑵若AE＝6，BC＝12，CD＝5，求AD的长.
 |
29.(本题满分10分)
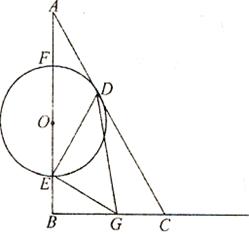
已知：如图，RtΔABC中，∠B＝90º，∠A＝30º，BC＝6cm.点O从A点出发，沿AB以每秒
cm的速度向B点方向运动，当点O运动了t秒(t>0)时，以O点为圆心的圆与边AC相切于点D，与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.
⑴若E与B不重合，问t为何值时，ΔBEG与ΔDEG相似？
⑵问：当t在什么范围内时，点G在线段BC上？当t在什么范围内时，点G在线段BC的延长线上？
⑶当点G在线段BC上(不包括端点B、C)时，求四边形CDEG的面积S(cm2)关于时间t(秒)的函数关系式，并问点O运动了几秒钟时，S取得最大值？最大值为多少？
 |
(南通市) 27、（本小题8分）
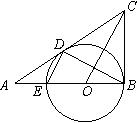
已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。
⑴从图中找出一对相似三角形（不添加任何字母和辅助线），并证明你的结论；
⑵若AD＝2，AE＝1，求CD的长。
(江苏省淮安市) 25．（本题满分10分）
已知：如图，在△ABC中，∠BAC的平分线AD交△ABC的外接圆⊙O于点D，交BC于点G。
（1）连结CD，若AG=4，DG=2，求CD的长；
（2）过点D作EF∥BC，分别交AB、AC的
延长线于点E、F。求证：EF与⊙O相切。
(常州市)
26．如图，点A、B、C、D在⊙O上，AB=AC，AD交BC于点E，AE=2，ED=4，求AB的长。
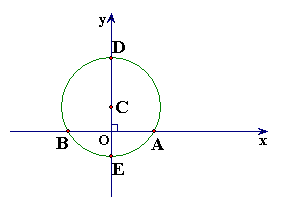
31．已知：如图，在平面直角坐标系中，点C在
轴上，以C为圆心，4cm为半径的圆与
轴相交于点A、B，与轴相交于D、E，且
。点P是⊙C上一动点（P点与A、B点不重合）。连结BP、AP。
（1）求∠BPA的度数；
（2）若过点P的⊙C的切线交轴于点G，是否存在点P，使△APB与以A、G、P为顶点的三角形相似？若存在，求出点P的坐标；若不存在，说明理由。