中考（数学）试题汇编方程部分
一、选择题：
1．（北京市东城区）关于x的方程
是一元二次方程，则（
）．
A．a＞0 B．a≠0 C．a＝1 D．a≥0
2．（北京市东城区）方程（x＋1）（x－2）＝0的根是（ ）．
A．x＝－1 B．x＝2 C．
D．
3．（北京市东城区）某型号的手机连续两次降价，每个售价由原来的1185元降到了580元．设平均每次降价的百分率为x，则列出方程正确的是（ ）．
A．
B．
C．
D．
4．（北京市石景山区）关于x的一元二次方程
的根的情况是（ ）
（A）有两个不相等的实数根 （B）有两个相等的实数根
（C）没有实数根 （D）无法确定
5．（北京市海淀区）一元二次方程x2－x＋2＝0的根的情况是（ ）
A．有两个相等的实数根 B．有两个不相等的实数根
C．无实数根 D．无法确定
6．（北京市海淀区）当使用换元法解方程
时，若设
，则原方程可变形为（ ）
A．y2＋2y＋3＝0 B．y2－2y＋3＝0
C．y2＋2y－3＝0 D．y2－2y－3＝0
7．（河北省）若x1，x2是一元二次方程2x2-3x+1=0的两个根，则
的值是
A．
B．
C．
D．
8．（湖南郴州市）方程
的左边配成完全平方后所得方程为（ ）
A.
B. 
C. 
D. 以上答案都不对
10．（浙江嘉兴市）若方程x2－4x＋m＝0有两个相等的实数根，则m的值是（ ）
（A）4 （B）－4 （C）
（D）
11．（南通市）一列列车自2004年全国铁路第5次大提速后，速度提高了26千米/时，现在该列车从甲站到乙站所用的时间比原来减少了1小时，已知甲、乙两站的路程是312千米，若设列车提速前的速度是x千米，则根据题意所列方程正确的是（ ）
A、
B、
C、
D、
12．（杭州市）方程
的正根的个数为（ ）
（A）0个 （B）1个 （C）2个 （D）3个
13．（浙江湖州市）已知一元二次方程x2 + 3x – 4 = 0的两个根为x1，x2，则x1·x2的值是（ ）
A. 4 B. -4 C. 3 D. –3
14．（浙江湖州市）方程组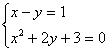
的解是（ ）
15．（常州市）用换元法解方程
时，设
，则原方程可化为（ ）
（A）
（B）
（C）
（D）
16．（常州市）关于
的一元二次方程
根的情况是（ ）
（A）有两个不相等实数根 （B）有两个相等实数根
（C）没有实数根 （D）根的情况无法判定
17．．（无锡市）若关于x的方程x2＋2x＋k＝0有两个相等的实数根，则k满足 ( )
A.k＞1 B.k≥1 C.k＝1 D.k＜1
18．（浙江金华市）方程（x2－3）2－5（3－x2）+2=0，如果设x2－3=y，那么原方程可变形为（ ）
A、y2－5y+2=0 B、y2+5y－2=0 C、y2－5y－2=0 D、y2+5y+2=0
19．（锦州市）设方程x2+x-2=0的两个根为α，β，那么(α-1)(β-1)的值等于( )
A.-4 B.-2 C.0 D.2
20．（锦州市）用换元法解方程
，若设
，则原方程可化为( )
A.y2-7y+6=0 B.y2+6y-7=0 C.6y2-7y+1=0 D.6y2+7y+1=0
21．．（无锡市）若关于x的方程x2＋2x＋k＝0有两个相等的实数根，则k满足( )
A.k＞1 B.k≥1 C.k＝1 D.k＜1
22．（宁波市）已知关于
的方程
有两个不相等的实根，那么
的最大整数
是（ ）
A．2 B．－1 C．0 D．1
23．（浙江富阳市）方程
的解是（ ）
A、
B、
C、
D、
24．（浙江富阳市）已知方程
的两根分别为
、
，则
的值是（ ）
A、
B、
C、
D、
25．（浙江富阳市）已知方程
有两个不相等的实数根，则
、
满足的关系式
是（ ）
A、
B、
C、
D、
26．（苏州市）西部山区某县响应国家“退耕还林”号召，将该县一部分耕地改还为林地。改还后，林地面积和耕地面积共有180km2, 耕地面积是林地面积的25%。设改还后耕地面积为x km2 ，林地面积为ykm2,则下列方程组中，正确的是 （ ）
A．
B．
C．
D．
27．（南京市）已知
是方程k x － y = 3的解，那么k的值是( )
A．2 B．－2 C．1 D．－1
28．（南京市）如果一元二次方程3x2―2x=0的两个根是x1、x 2，那么x1·x 2等于( )
A．2
B．0
C．
D．－
二、填空题：
1．（北京市朝阳区）已知方程
有两个相等的实数根，则m的值为________
2．（北京市东城区）已知2是方程
的一个根，则2a－1＝__________．
3．（河北省）用换元法解分式方程
时，如果设
，那么原方程可化为关于y的一元二次方程的一般形式是
.
4．（浙江嘉兴市）如果一个矩形的长和宽是一元二次方程x2－10x＋20＝0的两个根，那么这个矩形的周长是 。
5．（南通市）用换元法解方程
，若设
，则原方程可化为关于y的一元二次方程为
。
6．（常州市）已知一元二次方程
的两个根是
、
，则
= ，
=
，
=
。
7．（广东省）解方程
时．设
，则原方程化为y的整式方程
是_____________________
8．（无锡市）设x1、x2是方程x2－4x＋2＝0的两实数根，则x1＋x2＝ ，
x1·x2＝ .
9．（锦州市）若关于x的方程x2+5x+k=0有实数根，则k的取值范围是______.
10．（锦州市）方程组
的解是_____
.
11．（上海市）用换元法解
，可设
，则原方程可化为关于
的方程是______________．
12．（上海市）请设计一个二元二次方程组，使得这个二元二次方程组的解是
和 
试写出符合要求的方程组
13．（吉林省）已知m是方程
的一个根，则代数式
的值等于
.
三、解答题：
1．（北京市朝阳区）某校初三（2）班的师生到距离10千米的山区植树，出发1个半小时后，张锦同学骑自行车从学校按原路追赶队伍，结果他们同时到达植树地点．如果张锦同学骑车的速度比队伍步行的速度的2倍还多2千米．
（1）求骑车与步行的速度各是多少？
（2）如果张锦同学要提前10分钟到达植树地点，那么他骑车的速度应比原速度快
多少？
2．（北京市丰台区）用换元法解方程
3．（北京市丰台区）甲、乙两名工人接受相同数量的生产任务。开始时，乙比甲每天少做4件，乙比甲多用2天时间，这样甲、乙两人各剩120件；随后，乙改进了生产技术，每天比原来多做6件，而甲每天的工作量不变，结果两人完成全部生产任务所用时间相同。求原来甲、乙两人每天各做多少件？
4．（北京市东城区）解方程：
．
5．（北京市东城区）如果关于x的方程
没有实数根，试判断关于x的方程
的根的情况．
6．（北京市石景山区）用换元法解方程：
7．（北京市石景山区）某商场销售某种商品，第一个月将此商品的进价加价20%作为销售价，共获利6000元，第二个月商场搞促销活动，将商品的进价加价10%作为销售价，第二个月的销售量比第一个增加了100件，并且商场第二个月比第一个月多获利2000元，问此商品进价是多少元？商场第二个月共销售多少件？
8．（北京市海淀区）2004年4月我国铁路第5次大提速．假设K120次空调快速列车的平均速度提速后比提速前提高了44千米／时，提速前的列车时刻表如下表所示：
| 行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
| A地—B地 | K120 | 2：00 | 6：00 | 4小时 | 264千米 |
请你根据题目提供的信息填写提速后的列车时刻表，并写出计算过程．
| 行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
| A地—B地 | K120 | 2：00 | 264千米 |
9．（南通市）解方程组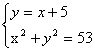
10．（南通市）已知关于x的一元二次方程
⑴请选取一个你喜爱的m的值，使方程有两个不相等的实数根，并说明它的正确性；
⑵设x1，x2是⑴中所得方程的两个根，求x1x2＋x1＋x2的值。
11．（杭州市）在ΔABC中，AB=AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F；设DE=
，DF=
，且实数，满足
，并有
；∠A使得方程
有两个相等的实数根
（1）试求实数，的值； （2）试求线段BC的长。
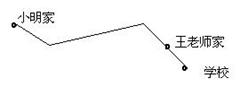
12．（重庆万州区）小明家、王老师家、学校在同一条路上，
小明家到王老师家的路程为3千米，王老师家到学校的路程
为0.5千米，由于小明的父母战斗在抗“非典”第一线，为
了使他能按时到校，王老师每天骑自行车接小明上学。已知
王老师骑自行车的速度是步行速度的3倍，每天比平时步行
上班多用了20分钟，问王老师的步行速度及骑自行车速度各
是多少千米/时？
13．（广东省）解方程组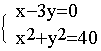
14．（广东省）某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，5月份的营业额达到633.6万元．求３月份到５月份营业额的平均月增长率．
15．（广东省）已知实数a、b分别满足
．求
的值.
16．（江西省）已知关于x的方程 x 2 – 2 ( m + 1 ) x + m 2 = 0
（1）当 m 取什么值时，原方程没有实数根；
（2）对 m 选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和。
17．（长春市）解方程组：
18．（长春市）小刚在商场发现他喜欢的随身听和书包单价之和是452元，并且随身听的单价比书包单价的4倍少8元.求小刚喜欢的随身听和书包的单价.
19．（泰州市）解方程：
20．（上海市）关于的一元二次方程
，其根的判别式的值为1，求
的值及该方程的根．
21．（上海市）为加强防汛工作，市工程队准备对苏州河一段长为2240米的河堤进行加固．由于采用新的加固模式，现在计划每天加固的长度比原计划增加了20米，因而完成此段加固工程所需天数将比原计划缩短2天．为进一步缩短该段加固工程的时间，如果要求每天加固224米，那么在现在计划的基础上，每天加固的长度还要再增加多少米？
22．（上海市）某公司要改制成股份公司，原来准备每人平均投资入股，正式统计时有10人表示不参加，因此其余每人要多分担1万元，到实际付款时，又有15人决定退出，这样最后余下的每人要再增加2万元，求统计入股之前有多少人准备入股？统计入股前每人应交多少万元？
23. （资阳市）已知关于x的方程 kx2-2 (k+1) x+k-1=0 有两个不相等的实数根，
(1) 求k的取值范围；
(2) 是否存在实数k，使此方程的两个实数根的倒数和等于0 ？若存在，求出k的值；若不存在，说明理由.
24．（苏州市）已知关于x的一元二次方程 ax2+x—a=0 ( a≠0 )
（1） 求证：对于任意非零实数a，该方程恒有两个异号的实数根;
（2） 设x1、 x2是该方程的两个根，若∣x1∣+ ∣x2∣=4，求a的值。
25．（扬州市）已知关于x的方程x2―(2k―3)x+k2+1=0。
①当k为何值时，此方程有实数根；
②若此方程的两实数根x1、x2满足： x1+ x2=3，求k的值。
26．（镇江市）已知关于x、y的方程组
有两组相同的实数解，求m的值。
27．（镇江市）已知，如图，Rt△ABC中，∠ACB=90º，AB=5，两直角边AC、BC的长是关于x的方程
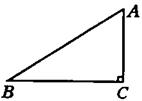x2―(m+5)x+6m=0的两个实数根。
①求m的值及AC、BC的长（BC>AC）；
②在线段BC的延长线上是否存在点D，使得以D、A、C为顶点的三角
形与△ABC相似？若存在，求出CD的长；若不存在，请说明理由。