中考模拟试题（一）
姓名： 成绩
一、填空题 （每题3分，共36分）
1、计算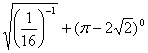
＝
。
2、如果
，那么m＝
。
3、把一个平角16等分，则每份为（用度、分、秒表示） 。
4、双曲线
的两个分支分别位于第 象限。
5、已知
，如果
，则
。
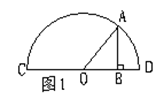
6、如图1，已知CD为半圆直径，AB垂直CD于B，设∠AOB＝α，则
= 。
7、已知当x＝2时，代数式
的值为6，那么当x＝－2时，代数式的值是 。
8、如图2，有一边长为
的正三角形，若要剪一张圆形纸片完全盖住这个图形，则这个圆形纸片的最小半径是 。
9、已知扇形的圆心角为150°，弧长为20π㎝，则这个扇形的半径为 cm。
10、已知二次函数
的图象与x轴交于
两点，则
。
11、已知
，则
。
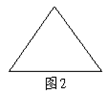
12、如图3，等腰直角△ABC的斜边AB所在的直线上有点E、F，且∠E+∠F＝45°，AE＝3，设AB＝x，BF＝y，则y关于x的函数关系式为 。
二、选择题 （每题3分，共24分）
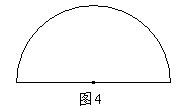13、对如图4所示的图形的三个说法：①是半图；②是弓形；③是扇形。其中正确的个数是（ ）
A、3
B、2
C、1
D、0
14、已知
，那么
的图象一定不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
15、若
，则函数
与
在同一平面直角坐标系中的图象大致是如图5中的（ ）
 |  |  | |||||
 | |||||||
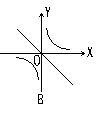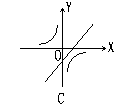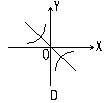16、为了考察一个养鸡场里鸡的生长情况，从中抽取8只鸡，称得它们的重量如下（单位：㎏） 2.9 3.1 3.0 3.1 3.2 3.3 2.8 3.4
在这个问题中
A、所抽取的8只鸡是总体的一个样本 B、养鸡场里所有鸡的总数是总体
C、样本容量是抽取的这8只鸡的重量 D、养鸡场里每只鸡的重量是个体
17、
表示直线，给出下列四个论断：（1）
∥
；（2）切⊙O于点A；（3）切⊙O于点B；（4）AB是⊙O的直径。若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为（ ）
A、1 B、2 C、3 D、4
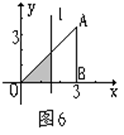
18、如图6，直角三角形AOB，AB⊥OB，且AB＝OB＝3。设直线
截此三角形所得的阴影部分的面积为S，则S与t之间的函数关系的图象为图7中的（ ）
 |  |  |  |  | |||||
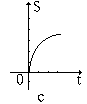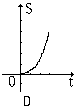19、给出五种图形：（1）矩形，（2）菱形，（3）等腰三角形（腰与底边不相等），（4）等边三角形，（5）平行四边形（不含矩形、菱形），其中可用两块能完全重合的含有30角的三角板拼成的所有图形是（ ）
A、（1）（2）（3） B、（2）（4）（5） C、（1）（3）（4）（5） D、（1）（2）（3）（4）（5）
20、在函数的图象上取点P，作PA垂直x轴于点A，作PB垂直y轴于点B，O为原点，且矩形OAPB的面积为2，则符合条件的P点共有（ ）
A、1个 B、2个 C、3个 D、4个
三、解答题（第21—24题，每题7分；第25—26题，每题10分；第27题12分，共60分）
21、计算题：
22、已知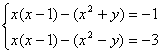
，求
的值。
23、解方程 
24、等腰三角形ABC的两腰AB、AC的长分别是方程
的两根，求k的值及底边BC的取值范围。
25、某地防汛部门为做好当年的防汛抗洪工作，根据本地往年汛期特点和当年气象信息分析，利用当地一水库的水量调节功能，制定当年的防汛计划：
从6月10日0时起，开启水库1号入水闸蓄水，每天经过1号水闸流入水库的水量为6万立方米；从6月15日0时起，打开水库的泄水闸泄水，每天从水库流出的水量为4万立方米；从6月20日0时起再开启水库2号入水闸，每天经过2号入水闸流入水库的水量为3万立方米；6月30日0时，入水闸和泄水闸全部关闭。根据测量，6月10日0时，该水库的蓄水量为96万立方米：
（1）设开启2号入水闸后的第x天的0时，水库的蓄水量为y万立方米，烈军属出y（万立方米）与x（天）之间的函数关系式（只要求写解析式）
（2）如果该水库的最大蓄水量为200万立方米，问该地防汛部门的当年汛期（6月30日0时）的防汛计划能否保证水库的安全（水库的蓄水量不超过水库的最大蓄水量）？请说明理由。
26、已知：如图8（1），PF是⊙O的切线，PE＝PF，A是⊙O上一点。直线AE、AP分别交于⊙O于点B、D，直线DE交⊙O于点C，联结BC。
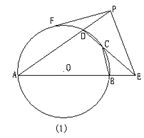
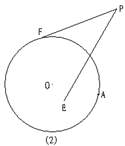
（1）求证：PE∥BC
（2）将PE绕点P顺时针旋转，使点E移到圆内，并在⊙O上另选一点A，如图8（2），其他条件不变，在图8（2）中画出完整的图形，此时PE与BC是否仍然平行？证明你的结论。
27、等腰梯形ABCD中，AD∥BC，AB＝DC，面积S=9，建立如图9所示的直角坐标系，已知A（1，0）、B（0，3）
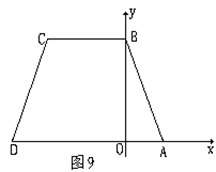
（1）求C、D两点的坐标；
（2）取点E（0，1），联结DE并延长交AB于点F，求证：DF⊥AB；
（3）将梯形
绕A点旋转180°到
，求对称轴平行于y轴，且经过A、
、
三点的抛物线解析式；
（4）是否存在这样的直线，满足以下条件：①平行于x轴，②与（3）中抛物有两交点，且这两交点和（3）中抛物线的顶点恰是一个等边三角形的三个顶点？若存在，求出这个等边三角形的面积，若不存在，请说明理由。