中考模拟数学试卷3
（考试时间100分钟 满分120分）
一 、选择题（每小题3分，共45分 每题中只有一个选项是正确的）
1.
计算
结果正确的是( )
A.
B.
C. 
D.
2. 如图表示了某个不等式的解集, 该解集所含的整数解的个数是( )
A. 4
B. 5
C. 6
D.7
3. 某项科学研究需要以30分钟为一个时间单位, 并记研究那天上午10时为0，10时以前记为负，10时以后记为正. 例如那天9:30记为－1，10:30记为1等等, 依此类推,那天上午7:30应记为( )
A. －3 B. －5 C. －2.30 D. －2.5
4. 两圆的半径分别是3和4, 圆心距是8, 则这两个圆的公切线有( )条
A. 1 B. 2 C. 3 D. 4
5. 两条不平行的直线被第三条直线所截,下列说法可能成立的是( )
A.同位角相等 B.内错角相等 C.同旁内角相等 D.同旁内角互补
6. 已知圆锥的底面半径是3, 高为4, 则这个圆锥侧面展开图的面积是( )
A. 12π B. 15π C. 20π D. 24π
7. 人民币1993年版的一角硬币正面图案中有一个正九边形, 如果设这个正九边形的半径为R, 那么它的边长是( )
A. Rsin20° B. Rsin40° C. 2Rsin20° D. 2Rsin40°
8. 如果最简二次根式
是同类二次根式, 那么使
有意义的x的取值范围是( )
A. x≤10 B. x≥0 C. x＜10 D. x＞0
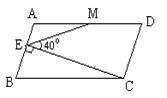
9. 如图，在□ABCD中，AD=2AB，M是AD的中点，CE⊥AB于点E，∠CEM=40°，则∠DME是（ ）
A. 150° B. 140° C. 135° D. 130°
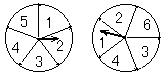
10. 如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时落在偶数上的概率是（ ）
A. 
B. 
C. 
D. 
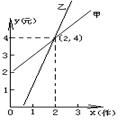
11． 如图是甲、乙两家商店销售同一种商品时，一次购买x (件)与需付款y (元)之间的函数图象, 下列说法：①购买两件时甲、乙两店售价相同； ②买1件时到乙店购买合算；③买3件时到甲店购买合算；④到乙店买1件约付款3元. 其中正确的说法是( )
A.①② B.②③④ C.②③ D.①②③
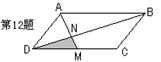12. 如图，在□ABCD中，如果点M为CD中点，AM与BD相交于点N，那么S△DMN∶S□ABCD为（ ）
A. 1∶12 B. 1∶9 C. 1∶8 D. 1∶6
13．如图，已知直角三角形ABC，CD是斜边AB上的高，那么下列各关系式：①
；②
；
③
；④
，其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
14．计算机利用的是二进制数，它共有两个数码0、1，将一个十进制数转化为二进制数，只需要把该数写成若干个2n数的和，依次写出1或0即可. 如十进制数19=16＋2＋1=1×24＋0×23＋0×22＋1×21＋1×20, 转化为二进制数就是10011, 所以19是二进制下的5位数. 问：2005是二进制下的几位数( )
A. 10 B. 11 C. 12 D. 13
15. 如果a、b、c为互不相等的实数, 且满足关系式
,
那么a的取值范围是( )
A. －1＜a＜5 B. a ＞－1 C. a＜－7 或a＞－1 D. a＜－1或a＞5
二、填空题(每小题4分,共20分)
16. 如图,已知∠ABC=30°,以O为圆心、2cm为半径作⊙O, 使圆心O在BC边上移动, 则当OB= cm时, ⊙O与AB相切.
17. 已知反比例函数
与一次函数
的图象的一个交点的纵坐标是－4, 则k的值是 ,
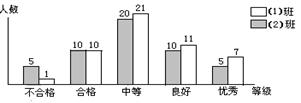
18. 下图反映了某校初二(1)、(2)两班各50名学生电脑操作水平等级测试的成绩,其中不合格、合格、中等、良好、优秀五个等级依次转化为50分、60分、70分、80分、90分,试结合图形计算: ①(1)班学生成绩众数是 分、中位数是 分; ②(2)班学生成绩的平均数是 分、方差是 .
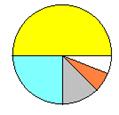
19. 如图是一张面积为1的圆形纸片，依次用不同色彩填涂圆面积的
，根据图形变化规律推断：当n为正整数时，
.
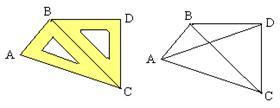
20. 将一副三角尺如图摆放一起,连接AD, 则∠ADB的余切值为 .
三、解答题(共55分, 每题都应有必要的解答过程)
21.(7分) 先将
化简, 然后自选一个合理的x值代入, 求出原式的值.
22.(8分) 自然数1到n的连乘积，用n！表示，这是我们还没有学过的新运算（高中称为阶乘），这种运算规定：1！=1 ，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，…
在这种规定下，请你解决下列问题：
（1） 
计算 5！=
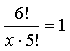
（2） 已知x为自然数 ，求出满足该等式的x：
（3） 分解因式 
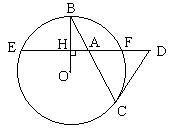
23.(8分) 如图已知OB是半径, 弦EF垂直OB于H, 点A是HF上的一点, BA和⊙O相交于另一点C, 过点C的切线和EF的延长线交于点D：(1)求证DA=DC; (2)当DF∶EF=1∶8, DF=
时, 求AB·AC的值.
24.(10分) 已知方程组
有两个不相等的实数解, (1)求k的取值范围; (2) 若方程组的两个实数解为
, 求出使得x1＋x1x2＋x2=1的k的值.
25. (10分) 据统计某外贸公司2003年、2004年的进出口贸易总额分别为3300万元和3760万元, 其中2004年的进口和出口贸易额分别比2003年增长20%和10%.
(1) 试确定2003年该公司的进口和出口贸易额分别是多少万元;
(2) 2005年该公司的目标是: 进出口贸易总额不低于4200万元, 其中出口贸易额所占比重不低于60%, 预计2005年的进口贸易额比2004年增长10%, 则为完成上述目标,2005年的出口贸易额比2004年至少应增加多少万元?
26.(12分) 如图,在直角坐标系中,以点P(1 ,－1)为圆心, 2为半径作圆, 交x轴于A、B两点, 抛物线
过点A、B, 且顶点C在⊙P上：
(1)
求⊙P上劣弧
的长;
(2) 求抛物线的解析式;
(3)
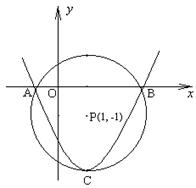在抛物线上是否存在一点D, 使线段OC与PD互相平分? 若存在, 求出点D的坐标; 若不存在,请说明理由.
考一模数学评分意见
一、选择题（本题有15个小题，每小题3分，共45分）
ABBDC BCAAC DADBB
二、填空题（本题有5个小题，每小题4分，共45分）
16. 4 17. －8 18. 70、70；70、120 19. 
20. 
三、解答题（共55分）
21.（7分）化简得x－2 ------4分 合理的值代入正确---3分。（取x=0或－1无意义，后3分不得）
22.（8分）（1）计算5！=120 -----2分 （只写出5×4×3×2×1 ---得1分）
（2）x=6 --------2分；
（3）（x－100）（x+99） ------4分；（如结论不对，过程有
=100×99可得2分）
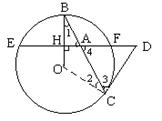23.（8分） （1）连结OC，则有∠1=∠2 ----1分， 又CD是切线，∴OC⊥CD, -----1分
而∠4与∠1互余，∠3与∠2互余，∴∠3=∠4，∴DA=DC -----2分
（2）∵DF=
,∴EF=8 -------1分，
又∵CD2=DF·DE=
=18 , ∴CD=3=AD -------1分
∴AF=3－=2 ,AE=6 --------1分
∴AB·AC=AE·AF=24 --------1分
24.（10分） （1）将②代入①整理 得 
（*） ----------------2分
∵方程组有两个不相等的实数解，即（*）式有两个不相等的根，∴△＞0
由△=
，
-------------------2分
又因为（*）式有两个不相等的根，k≠0 ∴
且k≠0 -------------------1分
（2）∵方程组有两个不相等的实数解，∴
是（*）式的两个根，
∴有
，
-------------2分，
由题意得 
+
=1
---------1分， k=－3 或 k=1 -------1分
∵ ，∴k=1舍去， k=－3 为所求。----------1分
25.（10分）设2003年进口贸易额为x万元、出口贸易额为y万元
则：
----------2分
------2分
∴ 2003年进口贸易额为1300万元、出口贸易额为2000万元
（2）设2005年的出口贸易额比2004年至少增加z万元
由2004年的进口贸易额是：1300（1+20%）=1560万元 ---------------1分
2004年的出口贸易额是：2000（1+10%）=2200万元 ----------------1分
则：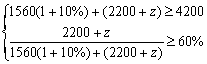
--------2分 解得
---------1分
所以z≥374 ，即2005年的出口贸易额比2004年至少增加374万元。 ---------1分
26.（12分） （1）作 PM⊥x轴，M为垂足, ∵MP=1,半径BP=2
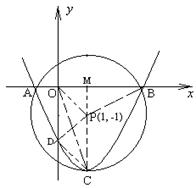∴∠MPB=60°
------------1分
∴∠APB=120° -----------1分
∴
·2=
------------1分
（2）由图可知C（1，－3），设抛物线顶点式
------------1分
点B(1+
, 0) 代入解得a=1 -------1分
∴
---------2分
（另解：写出两点A、B坐标，得两根式 
， -------2分，
结果
--------2分）
（3）假设存在点D使OC与PD互相平分，则四边形OPCD是□， --------1分
∴PC∥OD且PC=OD，∵PC∥y轴，∴D必在y轴上 -------1分
又∵PC=2，∴OD=2，即D（0，－2）， - -------1分
又D（0，－2）满足，∴ D在抛物线上---------------1分
所以存在D（0，－2）使线段OC与PD互相平分。 --------------1分
第一次中考模拟
数学 答题卷
一、选择题（本题有15个小题，每小题3分，共45分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
二、填空题(本题有5个小题，每小题4分，共20分)
16.
；
17. ；
18.① 分 、 分 ； ② 分 、 ；
19. ； 20. .
三、解答题(本大题共55分，应写出必要的解题过程)
21．（7分）先将化简, 然后自选一个合理的x值代入, 求出原式的值.
22.（8分）
(1)
(2)
(3)
23.（8分）
24.(10分) 已知方程组 有两个不相等的实数解： (1)求k的取值范围;
(2) 若方程组的两个实数解为, 求出使得x1＋x1x2＋x2=1的k的值.
25. (10分) 据统计某外贸公司2003年、2004年的进出口贸易总额分别为3300万元和3760万元, 其中2004年的进口和出口贸易额分别比2003年增长20%和10%.
(3) 试确定2003年该公司的进口和出口贸易额分别是多少万元;
(4) 2005年该公司的目标是: 进出口贸易总额不低于4200万元, 其中出口贸易额所占比重不低于60%, 预计2005年的进口贸易额比2004年增长10%, 则为完成上述目标,2005年的出口贸易额比2004年至少应增加多少万元?
26.(12分) 如图,在直角坐标系中,以点P(1 ,－1)为圆心, 2为半径作圆, 交x轴于A、B两点, 抛物线 过点A、B, 且顶点C在⊙P上：
(4)
求⊙P上劣弧的长;
(5) 求抛物线的解析式;
(6) 在抛物线上是否存在一点D, 使线段OC与PD互相平分? 若存在, 求出点D的坐标; 若不存在,请说明理由.