中考数学模拟试卷（10）
一、选择题（本大题共12小题，每小题3分，共36分． ）
1、在
中，有理数的个数是 （ ）
（A）2 （B）3 （C）4 （D）5
2、下列各式中，计算正确的是（ ）
A、
B、
C、
D、
3、方程
的根的情况是（ ）
A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定
4、函数
的自变量
的取值范围是（ ）
A、
且
B、
且
C、
且 D、
且
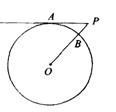5、如图，P为⊙○外一点，PA为⊙○的切线，OP交⊙○于B，设PA=，⊙○的半经为
，PB=2，则与的函数关系式为（ ）
A、
B、
C、
D、
6、某幼儿园准备用三种不同的多边形木板镶嵌地面，现有边长相同的正三角形和正八边形，还要边长相同的（ ）
A、正二十四边形 B、正十二边形 C、正八边形 D、正六边形
7、水果店用1000元购进一批草霉，当天售出，获利10％，过几天后又以上次售出价的
90％购进同样的草霉，由于大气变化卖不出去，一天后将这批草霉按第二次购进价的
九折（即90％）降价售出．这样、这家水果店在这两次交易中（ ）
（A）赢亏平衡 （B）赢利1元 （C）赢利9元 （D）亏本1.1元
8、若点
都是反比例函数
图象上的点，且x1<0<x2<x3，则下列各式中正确的是（ ）
（A）
（B）
（C）
（D）
9、下列命题：
（1）同圆的内接正四边形面积比内接正六边形的面积大.
（2）两圆半经分别为4和9，当两圆外切时它们的外公切线长为12.
（3）当两圆半经分别为2和3，且圆心距为5时，两圆共有3条公切线..
（4）600的圆心角所对的弧长等于圆周的
，其中正确的个数为（ ）.
A、l个 11、2个 C、 3个 D、4
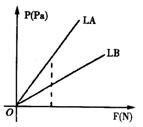
10、两个受力面积分别为为常数
为常数）的物体A、B，它们所受压强
与压力F（N） 的函数图象是射线
，如图，则（ ）
A SA>SB B SA<SB C SA=SB D SA与SB的大小无法确定
11、已知AB是⊙O的直径，AC、AD是弦，且AB=2，
，AD＝l，则圆周角
CAD
的度数是（ ）
A、
或
B、
C、
D、
或
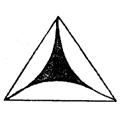
12、如图所示，某产品的商标由三个半径都等于R的半圆两两外切得到的图形的一部分，则切点间的弧所围成的阴影部分的面积是（ ）
（A）
（B）
（C）
（D）
二、填空题（本大题共8小题，每小题4分，共32分．把答案填在题中横线上．）
13、纳米是0.米，流感病毒的直径是90纳米，用科学记数法表示是______米．
14、从英语字母或汉字中，举四例既是轴对称又是中心对称的例子______.
15、用一张面积是S的矩形纸片，将对边重合围成圆柱，能得到一高一矮两个圆柱，它们的侧面积分别为
，那么
的数量关系是______。
16、
中，
，其周长值等于面积的值，则此三角形的内切圆面积为_______.
17、如图，已知AB是⊙O的直径，PC切⊙O于点C，
，则
等于____度.
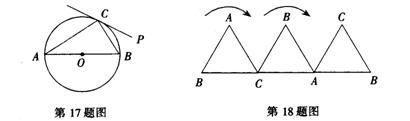
18、将形状为等边三角形的硬纸片沿水平线翻滚（如图所示），如果等边三角形的边长为1那么点B从开始位置到结束所走过的路径长度为＿cm（用含
的式子表示）．
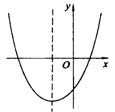
19、二次函数
的图象如右图所示，则点（
），在第_____象限.
20、观察下列分母有理化的计算：
；
；
……，从计算结果中找出规律，并利用这一规律计算：
…
＝ 。
三、解答题（本大题共8小题，共82分．解答应写出文字说明、证明过程或演骤）
21、（本小题满分8分）
计算：
-cos30
22、如图，将矩形ABCD（AB＜AD）沿BD折叠后，点C落在点E处，且BE交AD于点F.
（1） 若AB=4，BC=8，求DF的长
 |
（2）若DA平分∠EDB，求
的值
23(10分)、金星中学某班前年暑假将勤工俭学挣得的班费2000元按一年定期存入银行，去年暑假到后取出1000元寄往灾区，将剩下的1000元和利息继续按一年定期存人银行，待今年毕业后全部捐给母校，若今年到期后取得人民币（本息和）1155元，问银行一年定期存款的年利率（假定年利率不变）是多少？
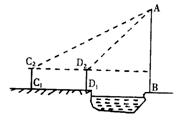24（10分）、如图，湖对岸有一电视塔AB，为测量它的高度，在
处用测角仪测得塔尖A的仰角为
，沿着塔的方向前进40米，到
处测得塔尖A的仰角为，已知测角仪高
米，求电视塔的高（不取近似值）．
25、 已知：方程
的解是
；
方程
的解是
；
方程
的解是
；
方程
的解是
；
问题：观察上述方程及其解，再猜想出方程
的解，并写出检验.
26．一次时装表演会预算中票价定为每张100元，容纳观众人数不超过2000人，毛利润y（百元）关于观众人数x（百人）之间的函数图像如图10-3所示，当观众人数超过1000人时，表演会组织者需向保险公司缴纳定额平安保险费5000元（不列入成本费用），请解答下列问题：
（1） 求当观众人数不超过1000人时，毛利润y关于观众人数x有函数解析式和成本费用S（百元）关于观众人数x的函数解析式.
（2）
若要使这次表演会获得36000元的毛利润，那么需售出多少张门票？需支付成本费用多少元？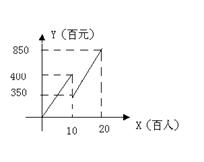
27、已知：如图1，∠ACG=90°，AC=2，点B为CG边上的一个动点，连结AB，将△ACB沿AB 边所在的直线翻折得到△ADB，过点D作DF垂直CG于点F.
（1）
当BC=
时，判断直线FD与以AB为直径的⊙O的位置关系，并加以证明
（2）
如图2，点B在CG上向点C运动，直线FD与以AB为直径的⊙O交于D、H两点，连结AH，当∠CAB=∠BAD=∠DAH时，求BC的长.
28、（本小题满分14分）
在直角坐标系xoy中，O为坐标原点，A，B，C，三点的坐标分别为A（5，0），B（0，4），C（-1，0）.点M和点N在x轴上（点M在点N的左边），点N在原点的右边，作MP垂直BN，垂足为P（点P在线段BN上，且点P与点B不重合），直线MP与y轴相交于点G，MG=BN.
（1） 求经过A，B，C三点的抛物线的解析式；
（2） 求点M的坐标；
（3） 设ON=t，△MOG的面积为s，求s与t的函数关系式，并写出自变量t的取值范围；
（4） 过点B直线BK平行于x轴，在直线BK上是否存在点R，使△ORA为等腰三角形，若存在，请直接写出点R的坐标；若不存在，请说明理由.