中考数学模拟试卷（三）
（时间：120分钟 满分：150分）（课改实验区）
班级________姓名___________号数________成绩_________等级__________
一、填空题（本题有12小题，每题3分，共36分）
1、2005的相反数是____________。
2、分解因式：4x2
1＝________.
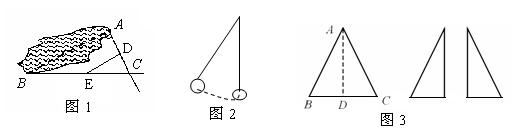
3、如图1，为了求出湖两岸A、B两点之间的距离，观测者测得DE=40m，且点D、E分别是线段AC、BC的中点，则A、B两点之间的距离为 _____m。
4、抛物线y=2(x-1)2+3的对称轴为 。
5、请你写出正视图、俯视图、左视图都相同的几何体的名称是____________(写出一种即可)
6、已知：⊙O1与⊙O2的半径分别为2cm和3cm，圆心距O1O2=5cm，则⊙O1与⊙O2的位置关系为______________。
7、抛掷一枚标有1、2、3、4的正四面体骰子，写出这个实验中的一个必然事件是 .
8、当k____________时，函数y=kx-1，y随x的增大而减少。
9、对甲、乙两台机床生产的零件进行抽样测量，其平均数、方差计算如下：机床甲：
甲=10，
甲=0.02； 机床乙：乙=10，乙=0.06由此可知：_________(填“甲”或“乙”)机床性能好。
10、为了更好识别每个学生所在的年级、班级，学校给每个学生制作胸卡并编号。其中前两位表示该生入学的时间，如现在的初一年是2004年入学的编为“04”；第3位用“1、2、3、…”表示所在班级；末两位代表座位号。那么现在初二年7班15号的小华同学的编码是________________。
11、如图2，某落地钟钟摆的摆长为0.6米,来回摆动的最大夹角为23º，钟摆在摆动的过程中,钟摆的运动路线为___________米(结果精确到0.01米)。
12、如图3，已知BC为等腰三角形纸片ABC的底边，AD⊥BC，AD=BC. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不全等的四边形的个数是______________。
二、选择题(本题有6小题，每题4分，共24分，每小题只有一个正确的答案．请把正确答案的字母代号填在括号内)
13、 的值为（ ）
A、±2 B、-2
C、+2 D、
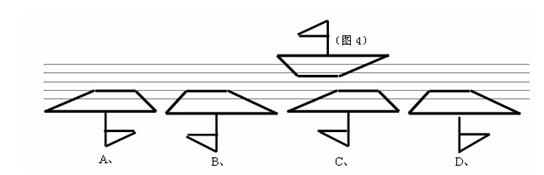14、如图1，是一只停泊在平静水面上的小船，它的“倒影”应是下列四幅图中的（ ）
15、为了能有效地使用电力资源，我市供电部门最近进行居民峰谷用电试点,每天8:00至21:00用电每千瓦时0.55元（“峰电”价），21:00至次日8:00每千瓦时0.30元(“谷电”价)。王老师家使用“峰谷”电后,五月份用电量为300千瓦时,付电费115元,则王老师家该月使用“峰电”（ ）。
A、100千瓦时 B、140千瓦时 C、160千瓦时 D、200千瓦时
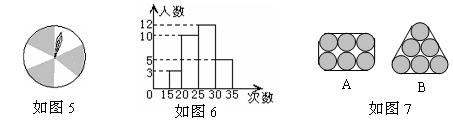
16、如图5所示的转盘，指针落在阴影部分的概率为（ ）
A、
B、 
C、
D、
17、为了了解本校九年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图6所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25~30次的频率是（ ）
A、0.1 B、0.2 C、0.3 D、0.4
18、如图7是分别按A、B两种方法用钢丝绳捆扎6 根圆形钢管的截面图，设AB所需钢丝绳的长度分别为a、b（不计接头部分），则a 、b 的大小关系为（ ）。
A、a＜b B、a＝b C、a＞b D、无法判断
三、解答题（本大题共8小题，满分70分，解答应写出文字说明、证明过程或推演步骤.）
19、(8分)
先化简下面的代数式,再求值：(x+1)2－2(x+2)， 其中
20、(8分) 已知：如图，点D、E在△ABC的边BC上，AB=AC,BD=EC.
求证：AD=AE
21、（8分）一布袋中有红、黄、白三种颜色的球各一个，它们除颜色外其它都一样.小亮从布袋中摸出一个球记录颜色后放回去摇匀，再摸出一个球.
（1）请你利用列举法（列表或画树状图）分析两次摸球所有可能出现的结果。
（2）求出小亮两次都能摸到白球的概率.
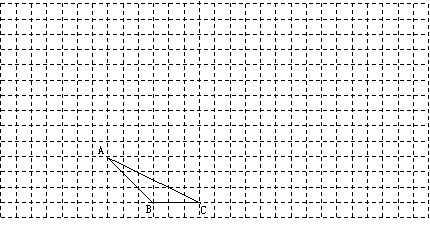
22、(满分8分)(1)请在如图所示的方格纸中，将△ABC向上平移3格，再向右平移6格，得△A1B1C1，再将△A1B1C1绕点B1按顺时针方向旋转90°，得△A2B1C2.
(2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度)，在你所建立的直角坐标系中，点C、C1、C2的坐标分别为：点C( )、点C1( )、点C2( )、
 |
23、(8分)某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例记录学期总评成绩，90分以上为优秀。甲、乙、丙三人的各项成绩如表（单位：分）。
请问：谁的学期总评成绩达到优秀？
| 纸笔测试 | 实践能力 | 成长记录 | |
| 甲 | 90 | 81 | 95 |
| 乙 | 88 | 90 | 95 |
| 丙 | 90 | 88 | 90 |
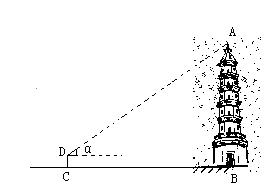24、(满分8分)泉州东西塔的“西塔”是中国现存最高的仿木结构楼阁式石塔，是全国重点文物建筑群的重要组成部分。在一次数学实践活动中，为了测量这座“西塔”的高度，小东在离塔底70米的C处(C与塔底B在同一水平线上)，用高1.4米的测角仪CD测得塔项A的仰角α=32°(如图)，求这座“千年塔”的高度AB(结果精确到0.01米).
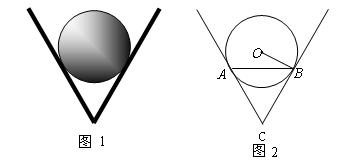25、(满分8分)如图1，一个圆球放置在V形架中.图2是它的平面示意图，CA和CB都是⊙O的切线，切点分别是A，B.如果⊙O的半径为
cm，且AB=6cm，求∠ACB.
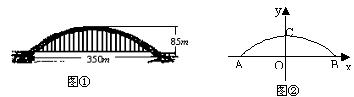
26、(满分8分)目前国内最大跨径的钢管混凝土拱桥——永和大桥，是南宁市又一标志性建筑，其拱形图形为抛物线的一部分（如图①），在正常情况下，位于水面上的桥拱跨度为350米，拱高为85米。
(1)在所给的直角坐标系中（如图②），假设抛物线的表达式为
，请你根据上述数据求出
、
的值，并写出抛物线的表达式（不要求写自变量的取值范围，、的值保留两个有效数字）。
(2)七月份汛期将要来临，当邕江水位上涨后，位于水面上的桥拱跨度将会减小，当水位上涨4
时，位于水面上的桥拱跨度有多大？（结果保留整数）
27、(13分)光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台，现将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区。两地区与该农机租赁公司商定的每天的租赁价格见下表：
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地区 | 1800元 | 1600元 |
| B地区 | 1600元 | 1200元 |
(1)设派往A地区χ台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y(元)，求y与χ间的函数关系式，并写出χ的取值范围；
(2)若使农机租赁公司这50台联合收割机，一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来；
(3)如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提出一条合理建议。
28、(13分)如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0），（3，4）。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥AC，交AC于P，连结MP。已知动点运动了x秒。
（1）P点的坐标为（____________， ____________）；（用含x的代数式表示）
（2）试求 ⊿MPA面积的最大值，并求此时x的值。
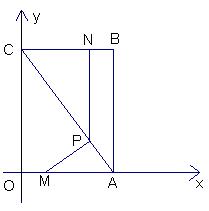（3）请你探索：当x为何值时，⊿MPA是一个等腰三角形？
你发现了几种情况？写出你的研究成果。