初中毕业会考暨高中阶段招生考试数学试卷

初中毕业会考暨高中阶段招生考试数学试卷

（课改区：市中区、威远县、隆昌县）

会考卷（100分）

一、选择题（每小题3分，共36分）

1．的相反数是（　　）

A．　　  B．3　　　 C．　　　　D．

2、方程x（x+1）=3（x+1）的解的情况是（　　）

　 A．x=-1　　　 B。x=3　　 C。　 D。以上答案都不对

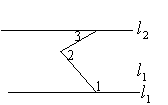
3、如图（1）所示，∥，∠1=120°，∠2=100°，则∠3=（　　 ）

  A．20°　　B。40°　　 C。50°　 D。60°

4．5个红球、4个白球放入一个不透明的盒子里，从中摸出6个球，恰好红球与白球都摸到，这件事情（　　）

A．不可能发生　　 B．可能发生　　 C．很可能发生　　 D．必然发生

5．在平面镜里看到其对面墙上电子钟示数如图所示：

那么实际时间是（　　）

A．21:05　　　 B．21:50　　  C．20:15　　　 D．20:51

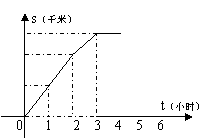6．某人骑车外出，所行的路程s（千米）与时间t（小时）的函数关系如图所示：

现有下列说法：

①第3小时中的速度比第1小时中的速度快；

②第3小时中的速度比第1小时中的速度慢；

③第3小时后已停止前进；

④第3小时后保持匀速前进。

其中说法正确的是（　　）

A．②③　  B．①④　　C．①③　　D．②④

7、一组数据按从小到大的顺序排列为1，2，3，x，6，9，这组数据的中位数是5，那么这组数据的众数为（　 ）

 A．4　　B。5　 C。5。5　　 D。6

8、如图（4），AC是⊙O的直径，∠BAC=20°，P是弧AB的中点，则∠PAB=（　 ）

A．35°　　B。40°　　 C。60°　 D。70°

9．右表给出的是本月份的日历表，

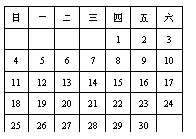任意圈出一横行或一竖列相邻的三个数，

这三个数的和不可能是（　　）

A．24　　　 B．43　　　

C．57　　　 D．69

10．有一长、宽、高分别为5cm、4cm、3cm的木箱，

在它里面放入一根细木条（木条的粗细、形变忽略不计）

要求木条不能露出木箱。请你算一算，能放入的细木条的最大长度是（　　）

A．　　　 B．　　　 C．　　　 D．

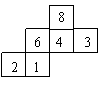
11．一个均匀的立方体各面上分别标有数字1，2，3，4，6，8，其表面展开图是如图所示，抛掷这个立方体，则朝上一面的数字恰好等于朝下一面上的数字的2倍的概率是（　　）

A．　　　　B．　　　　C．　　　　 D．

12、在如图（6）所示的梯形ABCD中，AB∥DC，AB=5，DC=11，①中A₁B₁是连结两腰中点的线段，易知A₁B₁=8，②中A₁B₁、A₂B₂是连结两腰三等分点且平行于底边的线段，可求出A₁B₁+A₂B₂的值……，照此规律下去，③中A₁B₁、A₂B₂，…A₁₀B₁₀是连结两腰十一等分点且平行于底边的线段，则A₁B₁+A₂B₂+…+ A₁₀B₁₀的值为（　 ）

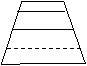
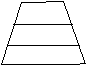
 A．50　　　　B．80　　　　C．96　　　　 D．100

二、填空题（每小题3分，共15分）

13．在2006年度“中国超级女生”的评选活动中，预计观众使用手机、小灵通或登陆网站参与评选投票将达到2350万人次，用科学计数法表示为___________人次。

14．若a+b=1, a－b=2006, 则。

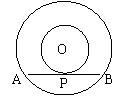
15、如图（7），在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为___________

16．某超市在“六一”期间开展有奖销售活动，凡购满100元商品的顾客可得奖券1张。本次活动共发放奖券1000张，经过摇奖产生一等奖1名，奖金400元；二等奖2名，奖金各200元；三等奖10名，奖金各50元。某人在这次活动中购满100元的商品，他中三等奖的概率是_______________。

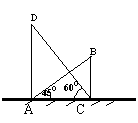
17．某学校的教学大楼和行政办公大楼相对而立，如图所示：

两楼间的距离AC=10cm,某学生在教学大楼底A处测得

行政办公大楼顶B处的仰角为45^O，

随后他又到行政办公大楼C处测得教学大楼顶D处的仰角为60^O，那么教学大楼比行政办公楼高_________m，

（精确到0.1,参考数据：）。

二、解答题：

18．（6分）计算：

19．（7分）化简求值：，其中，。

20．（8分）如图：正方形ABCD的对角线AC与BD相交于点O，且BE=CF，求证：

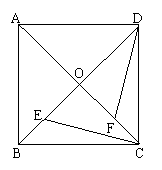①∠OEC=∠OFD。②CE=DF

21．（8分）某学校要印制一批宣传材料，甲印务公司提出收制版费900元，另外每份材料收印刷费0.5元；乙印务公司提出不收制版费，每份材料收印刷费0.8元。

（1）分别写出两家印务公司的收费y（元）与印制材料份数（份）之间的函数关系式。

（2）若学校预计要印5000份以内的宣传材料，请问学校应选择哪家印务公司更合算？

22．（10分）某校对九年学生进行“综合素质”评价，评价的结果分为A（优）B（良）C（合格）D（不合格）四个等级。现从中随机抽测了若干名学生的“综合素质”等级作为样本进行数据处理，并作出如下统计图。已知图中从左到右四个长方形的高的比为14:9:6:1。评价结果为D等级的有2人。请你回答以下问题：

（1）共抽测了多少人？

（2）样本中B等级的频率是多少？D等级的频率是多少？（精确到1%）

（3）若该校九年级的毕业生共390人，“综合素质”等级为A或B的学生才能报考重点高中。请你估计该校大约有多少名学生可以报考重点高中？

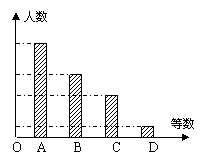（4）请你对该校九年级学生“综合素质”的整体情况作出简要评价。

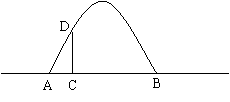
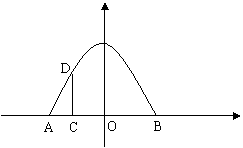23．（10分）如图所示，某建筑物有一抛物线形的大门，小强想知道这道门的高度。他先测出门的宽度AB=8m，然后用一根长为4m的小竹竿CD竖直地接触地面和门的内壁，并测得AC=1m。小强画出了如图的草图，请你帮他算一算门的高度OE（精确到0。1m）。

加试卷

一、填空题（每小题4分，共20分）

1．已知，则。

2、已知圆心在y轴上的两圆相交于A（2x+y，-2）和B（4，x+2y）两点，那么x+y=_________

3．甲、乙两人按如下规则做游戏：桌面上的七只铅笔，每次可取一支或二支，由甲先取，最后取完铅笔者获胜。如果甲获胜的概率为1，则甲第一次应取走铅笔_______支；如果桌上铅笔多于七支，仍由甲先取，若乙获胜的概率为1，则桌上至少要有铅笔__________支。

4、已知菱形ABCD上每一点的坐标都满足，则菱形ABCD的面积是_______

5．杨经理要从B市到D市去联系业务，准备乘飞机前往。某航空公司经营A、B、C、D四个城市之间的客运业务，其部分机票价格如下：A市到B市2000元，A市至C市1600元，A市至D市2500元，B市至C市1200元，C市至D市900元。已知机票价格与两城市之间的距离成正比，这四个城市中位于同一直线上的是____________三个城市，杨经理由B市直飞D市的机票价格是____________元。

二、解答题（每小题10分，共30分）

6．如图：四边形ABCD中，E、F、G、H分别为各边的中点，顺次连结E、F、G、H，把四边形EFGH称为中点四边形。连结AC、BD，容易证明：中点四边形EFGH一定是平行四边形。

（1）如果改变原四边形ABCD的形状，那么中点四边形的形状也随之改变，通过探索可以发现：当四边形ABCD的对角线满足AC=BD时，四边形EFGH为菱形；

当四边形ABCD的对角线满足_______________时，四边形EFGH为矩形；

当四边形ABCD的对角线满足________________时，四边形EFGH为正方形。

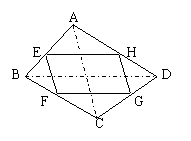（2）探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系，请写出你发现的结论，并加以证明。

（3）如果四边形ABCD的面积为2，那么中点四边形EFGH的面积是多少？

生产A种产品件数	生产B种产品件数	用工时间（分）
1	1	35
3	2	85

7．某工厂工人的工作时间为每月25天，每天8小时，该厂生产A、B两种产品。每位工人每月有基本工资400元，工人每生产一件A种产品，可得报酬0.75元，每生产一件B种产品，可得报酬1.40元。下表记录了工人小李的工作情况：

（1）小李每生产一件A和B种产品，分别需要多少时间？

（2）求小李每月工资额的范围。

8．阅读并解答下面问题：

（1）如图所示，直线l的两侧有A、B两点，在l上求作一点P，使AP+BP的值最小（要求尺规作图，保留作图痕迹，不写画法和证明）

（2）如图A、B两个化工厂位于一段直线形河堤的同侧，A工厂至河堤的距离AC为1km，B工厂到河堤的距离BD为2km，经测量河堤上C、D两地间的距离为6km.现准备在河堤边修建一个污水处理厂，为使A、B两厂到污水处理厂的排污管道最短，污水处理厂应建在距C地多远的地方？

（3）通过以上解答，充分展开联想，运用数形结合思想，请你尝试解决下面问题：若，当为何值时，的值最小，并求出这个最小值。