机密 ★ 启用前
初中第五学期末教学质量测试
数 学（非实验区）
本试卷分为试题卷和答题卷两部分，其中试题卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）组成，共4页；答题卷共4页.满分100分.考试结束后将答题卡和答题卷一并交回.
第Ⅰ卷(选择题, 共30分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,不能答在试题卷上.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出填涂在答题卡上.
1.下列关于x的方程,有两个不相等的实数根是
A.x²-6x+9=0 B. x²+5x+7=0
C.2x²-4x+1=0 D.-3x²-6x-5=0
2.考查下列命题:
(1)和已知线段两个端点距离相等的点的轨迹是这条线段的中线;
(2)经过不在同一直线的4个(或4个以上)的点都能作圆;
(3)圆的对称轴是直径;
(4)平分弦(不是直径)的直径垂直于弦;
(5)如果两条弧相等,那么它们所对的弦、弦心距、圆心角和圆周角都相等.
其中正确的有
A.4个 B.3个 C.2个 D.1个
3.在Rt△ACB中,∠C为直角,CD⊥AB于点D,cos∠B=4:5,则tan∠ACD=
A.3:4 B.4:3 C.4:5 D.5:4
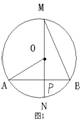
4.如图1,⊙O的直径MN⊥AB于点P,∠BMN=30º,则∠AON=
A.15º B.30º
C.45º D.60º
5.若方程
有增根，则m的值为
A.-2或0 B.2或0
C.1或
D. -1或
6.某电视机产品经过两次降价后(每次降价的百分率都为20%),每台的价格降至1600元;春节期间,由于市场景气,该品又经过两次提价(每次提价的百分率都为25%),那么两次提价后该品每台的价格与两次降价前相比
A.有所上涨 B.有所下降 C.不涨不降 D.无法确定
7.已知点P（a，3）与点M（2，β）经过直线y=4x+b，且a与反比例函数
的比例系数k相等，此反比例函数又经过点N（tan60º,-cos30º）,则点M（2，β）关于y轴对称的点的坐标为
A．(-2,17) B.(-2,13) C.(-2,11) D.(-2,-11-
)
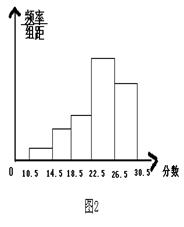8.某校为了了解学生的身体素质情况,对初三（1）班的
50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目的满分为10分.如图2,是将该班学生所得的三项成绩(成绩均为整数)进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12, 0.46.下列说法:①学生的成绩≥27分的共有15人;②学生的成绩的众数在第四小组(22.5-26.5)内;③学生的成绩的中位数在第四小组(22.5-26.5)内.其中正确的说法是
A.①② B.①③ C.②③ D.①②③
9.数据8,10,12,9,11的平均数和标准差分别是
A.10和
B.10和2 C.50和 D.50和2
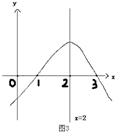
10．已知二次函数y=ax²+bx+c的图象如图3示，对称轴为 x=2，则下列说法错误的是
A．a+b+c=0 B.b²-4ac>0
C. 16a+4b+c>0 D. abc>0
第Ⅱ卷(非选择题,共70分)
注意事项:
1． 用钢笔或圆珠笔将答案直接写在答题卷上.
2． 答卷前将答题卷的密封线内项目填写清楚.
二、填空题:本大题共8小题,每小题3分,共24分.把答案填在题中横上.
11.将2x²-3xy-4y²分解因式为 ;
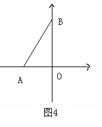
12.如图4,在直角坐标系中,点A、B的坐标分别是(m,0)和(0,n),且m,n(m<n)为x²-14x+48=0的两根,则Rt△AOB内心的坐标为____________;
13.将抛物线y=2x²-8x+5先向上平移8个单位,再向右平移
7个单位得到的抛物线为 ;
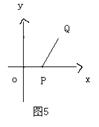
14.如图5,点P的坐标为(1,0), ∠QPO=120º,函数y=kx+b
的图象经过P,Q两点,则此函数的解析式为_____________;
15.若tana,cota是方程kx²-10x-4=0的两根,且sina+cosa=k,则sina·cosa= _______;
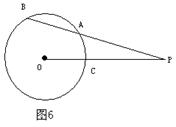
16.如图6,P为⊙O外一点,割线PAB交⊙O于A、B,若PO=10,
且PA²=36-PA·AB,则⊙O的半径为___________;
17.直线y=-x+2与双曲线y=-
的交点不在________象限
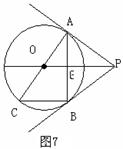
18.如图7,PA,PB是⊙O的切线,A,B是切点,AC是⊙O的直径,
OP与AB相交于点E,AC为4,PE为3,那么BC的长是___;
三、解答题:本大题共6小题,共46分.解答应写出文字说明、证明过程或演算步骤.
19.(本题满分8分)已知关于x的方程x²+(8-4m)x+4m²=0.
(1)若方程有两个相等的实数根，求m的值，并解这时的方程；
(2)是否存在正数m，使方程的两个实数根的平方和等于136？
若存在，请给出满足条件的m的值；若不存在，请说明理由.
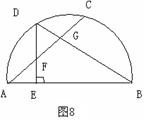
20.(本题满分7分)如图8,已知AB是半圆的直径,AC是一条弦,D是弧AC的中点,DE⊥AB于E,交AC于F,DB交AC于G,试猜想点F在AG上的位置,并给出证明.
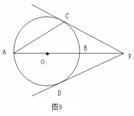21.(本题满分7分)如图9,AB是⊙O的直径,P在AB的延长线上,PD与⊙O相切于D,C在⊙O上,PC=PD.
(1)求证:PC是⊙O的切线;
(2)连接AC,若AC=PC,PB=1,求⊙O的半径.
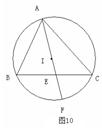
22.(本题满分8分)如图10,点I是△ABC的内心,AI交BC于E,交△ABC的外接圆于点F.
求证: (1) IF=BF=CF.
(2) IF²=AF·EF.
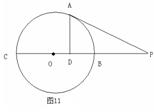23.(本题满分8分)如图11,已知PA和⊙O相切于A,PO交⊙O于B、C两点,AD⊥PO,D为垂足,求证:OB·CP=CD·OP.
24.(本题满分8分)心理学家通过实验发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分，且0≤x ≤30）之间成二次函数关系，y值越大，表示接受能力越强，已知
在一次实验中，对某学生此能力的三次调查结果如下表：
| x | 0 | 10 | 20 |
| y | 43 | 59 | 55 |
(1)求y与x的函数关系式；
(2)在第几分钟时，学生的接受能力最强，最强的接受能力为多少；
(3)x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？