中考数学试题2课改实验区）
考试时间120分钟，试题满分150分
一、选择题（每小题3分，共24分）
1．下列物体中，主视图为图1的是（ ）
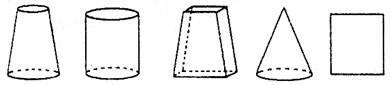
Ａ． Ｂ． Ｃ． Ｄ． 图1
2．下列计算中，正确的是（ ）
A．
B．
C．
D．
3．图2是几种汽车的标志，其中是轴对称图形的有（ ）
A．1个 B．2个 C．3个 D．4个
4．数据1，6，3，9，8的极差是（ ）
A．1 B．5 C．6 D．8
5．把不等式组
的解集表示在数轴上，正确的是（ ）
 |
6．下列事件：（1）阴天会下雨；（2）随机掷一枚均匀的硬币，正面朝上；（3）12名同学中，有两人的出生月份相同；（4）2008年奥运会在北京举行．其中不确定事件有（ ）
A．1个 B．2个 C．3个 D．4个
7．估算
的值（ ）
A．在5和6之间 B．在6和7之间
C．在7和8之间 D．在8和9之间
8．已知点
为
的内心，
，则
的度数是（ ）
A．
B．
C．
D．
二、填空题（每小题3分，共24分）
9．2006年是我国公民义务植树运动开展25周年，25年来我市累计植树株，这个数字可以用科学记数法表示为 株．
10．分解因式：
．
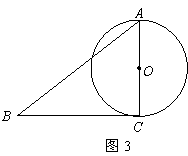
11．如图3，已知的一边
与以
为直径的
相切于点
，若
，则
= ．
12．如果反比例函数
的图象位于第二、四象限内，那么满足条件的正整数
的值是 ．
13．已知等腰三角形
中，
为边上一点，连接
，若
和
都是等腰三角形，则
的度数是 ．
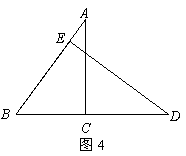
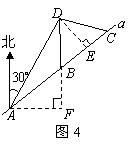
14．如图4，已知
，
，则
．
15．观察下列等式：
，
，
，
，
，
，
，……．通过观察，用你所发现的规律确定
的个位数字是 ．
16．如图5，已知在中，直径
，正方形
的四个顶点分别在半径
，
以及上，并且
，则
的长为 ．
三、（第17小题6分，第18、19小题各8分，第20小题10分，共32分）
17．
计算：
．
18．先化简，再求值：
，其中
．
19．如图6，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．如图6中的称为格点．
 |
（1）如果
两点的坐标分别是
和
，请你在方格纸中建立平面直角坐标系，并直接写出点
，点的坐标；
（2）请根据你所学过的平移、旋转或轴对称等知识，说明图6中“格点四边形图案”是如何通过“格点图案”变换得到的．
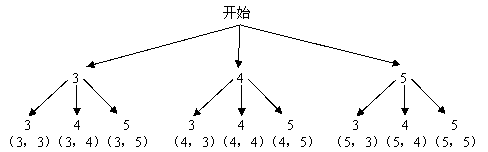
20．一个不透明的袋子中装有三个完全相同的小球，分别标有数字3，4，5．从袋子中随机取出一个小球，用小球上的数字作为十位上的数字，然后放回，再取出一个小球，用小球上的数字作为个位上的数字，这样组成一个两位数．试问：按这种方法能组成哪些两位数？十位上的数字与个位上的数字之和为9的两位数的概率是多少？用列表法或画树状图法加以说明．
四、（每小题10分，共20分）
21．某工程队在我市实施棚户区改造过程中承包了一项拆迁工程，原计划每天拆迁
，因为准备工作不足，第一天少拆迁了20%．从第二天开始，该工程队加快了拆迁速度，第三天拆迁了
．
求：（1）该工程队第一天拆迁的面积；
（2）若该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数相同，求这个百分数．
22．学校鼓励学生参加社会实践，小萌所在班级的研究性学习小组在假期对她们所在城市的一家晚报的读者进行了一次问卷调查，以便了解读者对该种报纸四个版面的喜欢情况．她们调查了男女读者各500名，要求每个读者选出自己最喜欢的一个版面，并将得到的数据绘制了下面尚未完成的统计图．
 |
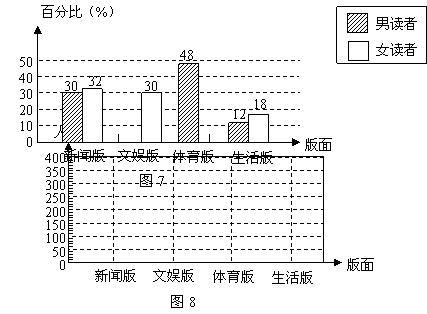（1）请直接将图7所示的统计图补充完整；
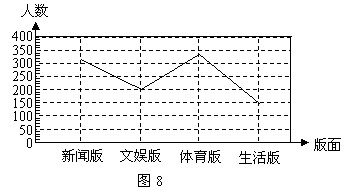
（2）请分别计算出喜欢各版面的总人数，并根据计算结果利用图8画出折线统计图；
（3）请你根据上述统计情况，对该报社提出一条合理化建议．
五、（12分）
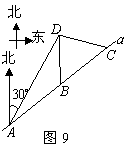
23．如图9，某市郊外景区内一条笔直的公路
经过三个景点
．景区管委会又开发了风景优美的景点
．经测量景点位于景点
的北偏东
方向
处，位于景点的正北方向，还位于景点的北偏西方向上．已知
．
（1）景区管委会准备由景点向公路修建一条距离最短的公路，不考虑其他因素，求出这条公路的长．（结果精确到0.1km）
（2）求景点与景点之间的距离．（结果精确到1km）
（参考数据：
，
，
，
，
，
，
．）
六、（12分）
24．某企业信息部进行市场调研发现：
信息一：如果单独投资种产品，则所获利润
（万元）与投资金额
（万元）之间存在正比例函数关系：
，并且当投资5万元时，可获利润2万元．
信息二：如果单独投资种产品，则所获利润
（万元）与投资金额（万元）之间存在二次函数关系：
，并且当投资2万元时，可获利润2.4万元；当投资4万元时，可获利润3.2万元．
（1）请分别求出上述的正比例函数表达式与二次函数表达式；
（2）如果企业同时对
两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？
七、（12分）
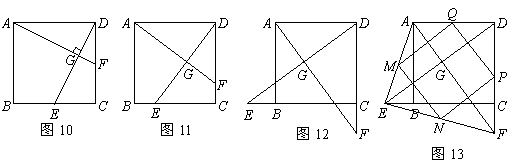
25．如图10，在正方形中，点
分别为边
的中点，
相交于点
，则可得结论：①
；②
．（不需要证明）
（1）如图11，若点不是正方形的边的中点，但满足
，则上面的结论①，②是否仍然成立？（请直接回答“成立”或“不成立”）
（2）如图12，若点分别在正方形的边
的延长线和
的延长线上，且，此时上面的结论1，2是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由．
（3）如图13，在（2）的基础上，连接
和
，若点
分别为
的中点，请判断四边形
是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程．
 |
八、（14分）
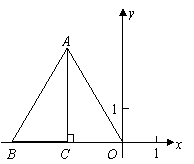
26．如图14，在平面直角坐标系中，两个全等的直角三角形的直角顶点及一条直角边重合，点在第二象限内，点，点在轴的负半轴上，
．
（1）求点的坐标；
（2）如图15，将
绕点按顺时针方向旋转到
的位置，其中
交直线
于点
，
分别交直线
于点
，则除
外，还有哪几对全等的三角形，请直接写出答案；（不再另外添加辅助线）
（3）在（2）的基础上，将绕点按顺时针方向继续旋转，当
的面积为
时，求直线
的函数表达式．
 |  | ||
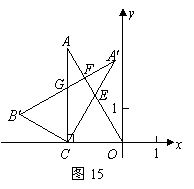中考数学试题2课改实验区）参考答案
一、选择题（每小题3分，共24分）
1．B 2．D 3．B 4．D 5．A 6．C 7．C 8．C
二、填空题（每小题3分，共24分）
9．
10．
11．
12．
13．
或
14．
15．
16．5
三、（第17小题6分，第18，19小题各8分，第20小题10分，共32分）
17．解：原式
．
18．解：原式
．
当时，原式
．
19．（1）如图1
，
．
（2）把“格点图案”向右平移10个单位长度，再向上平移5个单位长度，以点
为旋转中心，按顺时针方向旋转
，即得到“格点四边形图案”．
20．解：方法一
|
 | 3 | 4 | 5 | ||||
| 3 | （3，3） | （3，4） | （3，5） | ||||
| 4 | （4，3） | （4，4） | （4，5） | ||||
| 5 | （5，3） | （5，4） | （5，5） |
方法二
因此，能组成的两位数有：33，34，35，43，44，45，53，54，55．
组成的两位数有9个．
其中，十位上数字与个位上数字之和为9的两位数有两个，
（十位上数字与个位上数字之和为9的两位数）
．
四、（每小题10分，共20分）
21．解：（1）
，
所以，该工程队第一天折迁的面积为
．
（2）设该工程队第二天，第三天每天的拆迁面积比前一天增长的百分数是，
则
．解得
（舍）
所以，该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是20%．
22．（1）答案见图2，共计2分
 |
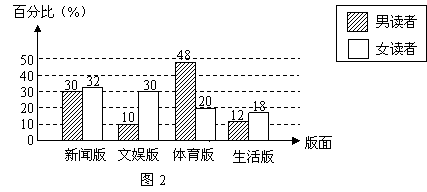（2）新闻版：
（人）
文娱版：
（人）
体育版：
（人）
生活版：
（人）
绘制的折线的统计图如图3：
 |
（3）积极向上、有意义即可．
五、（12分）
23．解：（1）如图4，过点作
于点，
过点作
，交
的延长线于点
．
在
中，
，
．
．
在
中，
．
．
．
在
中，
，
，
．
．
景点向公路修建的这条公路的长约是3.1km．
（2）由题意可知
，
由（1）可知
，所以
，
，
在
中，
，
．
景点与景点之间的距离约为4km．
六、（12分）
24．解：（1）当
时，
，
，当
时，
；当
时，
．
解得
．
（2）设投资种商品万元，则投资种商品
万元，获得利润
万元，根据题意可得
当投资种商品3万元时，可以获得最大利润5.8万元，所以投资种商品7万元，种商品3万元，这样投资可以获得最大利润5.8万元．
七、（12分）
25．解：（1）成立；（2）成立．
四边形是正方形，
,
．
又
，
．
．
又
，
．
，
．
（3）正方形．
证明：
，
，
同理
，
．
四边形是平行四边形．
又
，
．
又
，
．
平行四边形是菱形．
．
又
，
．
，
菱形是正方形．
八、（14分）
26．解：（1）在
中，，
．
点的坐标为
．
（2）
，
，
．
（3）如图5，过点
作
于点
．
，
．
在
中，
，
，
．
点的坐标为
．
设直线
的函数表达式为
，则
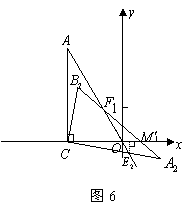
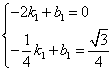解得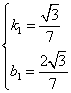
．
同理，如图6所示，点
的坐标为
．
设直线
的函数表达式为
，则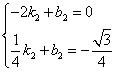
解得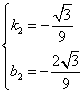
，
．
|