初三数学第一学期教学质量调查问卷
初 三 级 数 学
说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分共130分,考试时间80分钟.
第Ⅰ卷（选择题 共30分）
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.
的值等于（ ）
A.
. B.
.
C.
.
D.
.
2.若
是锐角，且
，则
的度数是（ ）
A.
. B.
.
C.
. D.
.
3. 函数
的自变量
的取值范围是（ ）
A.
. B.
.
C.
. D.
.
4.点
在（ ）
A.第一象限. B.第二象限. C.第三象限. D.第四象限.
5.已知⊙O的半径为
，圆心O到直线
的距离为
，直线
和⊙O相离时，下面式子正确的是（ ）
A.
. B.
. C.
. D.
.
6.方程
的根的情况是（ ）
A.有一个实数根. B.有两个相等的实数根.
C.没有实数根. D.有两个不相等的实数根.
7.用配方法将二次三项式
变形的结果是（ ）
A.
.
B.
.
C.
.
D.
.
8.一次函数
的图象不经过的象限是（ ）
A.第一象限. B.第二象限.
C.第三象限. D.第四象限.
9.如图，A、B、C三点都在⊙O上，点D是AB延长线上一点，∠AOC
，则∠CBD的度数是（ ）
A.
. B.
.
C.
. D.
.
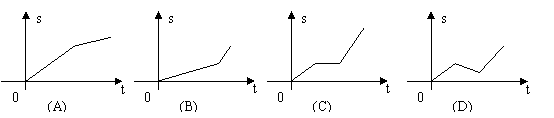
10.李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下来修车，车修好后，因怕耽误上学时间，于是就加快了车速，如图所给出的四个函数示意图象中（
为距离，
为时间），符合以上情况的是（
）．
第Ⅱ卷（非选择题 共100分）
学校： 班别： 姓名： 学号：
| 题目 | 二 | 三 | 四 | 五 | 六 | 总 分 | |||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |||
| 分数 | |||||||||||||
二、填空题(本大题共5小题,每小题3分,共15分.把答案填在题中横线上)
11.方程
的解是
.
12.经过线段AB的两个端点A、B的圆的圆心轨迹是 .
13.一条弦把圆分为2：3的两部分，那么这条弦所对的圆周角的度数是 .
14.如图，已知AB为⊙O的直径，且AB⊥CD，垂足为M，CD=8，AM=2，则OM= .
15.李老师在课堂上给出一个二元方程
，让同学们找出它的解.小刘写出的解是
小张写出的解是
请你找出与小刘、小张的解都不同的一组解
.
三、解答题(每小题6分，共30分).
16.计算：
.
17.解方程组：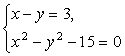
18.下图是某地一天的温度随时间变化的图象，观察图象，回答下列问题：
（1）最高温度与最低温度相差多少度？
（2）指出气温在什么时段上升，什么时段下降？
 |
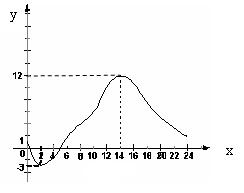19.制作铁皮桶，需要在一块三角形余料上截取一个面积最大的圆，请你画出该圆.(尺规作图，不写作法、证明和讨论,但要保留作图痕迹).
20.已知，如图，AB、CD、EF是⊙O的三条弦，且AB∥CD∥EF.求证：△ACE≌△BDF.
四、解答题(第21、22题每题8分，第23、24题每题9分，共34分)
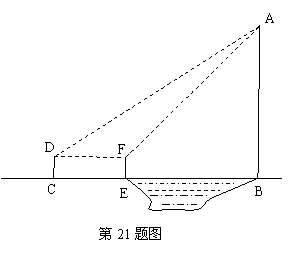21.如图，河对岸有高层建筑物AB，为测其高，在C处，由点D用测量仪则得顶端A的仰角为
，向高层建筑物前进50米，到达E处，由点F测得顶点A的仰角为
,已知测量仪高CD=EF=1.2米，求高层建筑物AB的高.(
，
)
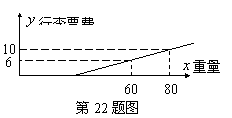22.某地长途汽车客运公司规定旅客可随身携带一定重量的行李，若超过规定，则需要购买行李票，行李票费
（元）是行李重量
（千克）的一次函数，其图象如图所示，求：
（1）与间的函数关系式；
（2）旅客最多可免费携带行李的千克数.
23.小明是一位刻苦学习、勤于思考、勇于创造的同学．一天，他在解方程时，突然产生了这样的想法：
这个方程在实数范围内无解，如果存在一个数
使
，那么方程可以变为
，则
，从而是方程的两个根．小明还发现具有如下性质：
请你观察上述等式，根据发现的规律填空：
，
，
．（
为自然数）．
24.已知，如图，AD是△ABC的边BC上的高，AE是△ABC的外接圆直径.
求证：（1）△ADB∽△ACE； （2）AB·AC=AD·AE.
五、解答题（25题10分，26题11分，共21分）
25.已知：关于的方程
的两个实数根的倒数和等于3，关于的方程
有实数根，且
为正整数.求代数式
的值.
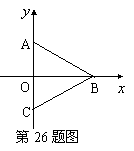26.如图,△ABC的边AC在
轴上，AC的中点为原点O,顶点B的坐标为（3，0），直线AB的解析式为
.
（1）求的值；
（2）已知点M是△ABC内切圆的圆心，求M点的坐标；
（3）以O为圆心的圆与直线AB、CB都相切，试求⊙O的半径.