初三数学模拟试卷(一)
一、选择题: 本大题共12小题；每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．
的相反数是 【 】
A．
B．
C．
D．
2．据有关资料，当前我国的道路交通安全形势十分严峻，去年我国交通事故的死亡人数约为１０。４万人，居世界第一，这个数用科学记数法表示是 （ ）
Ａ。1。04×104 Ｂ1。04×105
Ｃ1。04×106
Ｄ10。4×104
3．点P(1，―2)关于y轴对称的点的坐标是（ ）
A (―1，―2) B (1， 2) C (―1，2) D (―2，1)
4．不等式组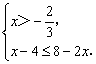
的最小整数解是（ ）
（A）－1 （B）0 （C）1 （D）4
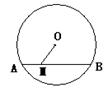
5．如图，⊙Ｏ的半径为５，弦ＡＢ的长为８，Ｍ是弦ＡＢ上的动点，则线段ＯＭ长的最小值为（ ）
Ａ。２ Ｂ。３ Ｃ。４ Ｄ。５
6．如图1，把一个正方形三次对折后沿虚线剪下则得到的图形是 ( )
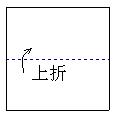
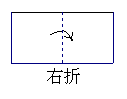
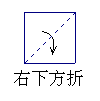
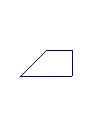
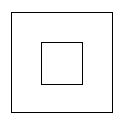
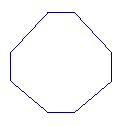
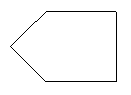
A B C D
7．如图，□ABCD的周长为16cm，AC、BD相交于点O，
OE⊥AC交AD于E，则△DCE的周长为（ ）
A．4 cm B．6cm C．8cm D．10cm
8、如图：在△ABC中，∠A=30°，tanB=
，AC=
，则AB的长是（ ）
A、3+
B、2+2 C、5 D、
9、已知实数x满足x2+
+ x+
=0,那么x+的值为 （ ）
A、1或-2 B、-1或2 C、1 D、-2
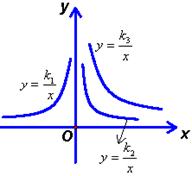10．如图2是三个反比例函数
在x轴上方的图象，由此观察得到
的大小关系为
A．
>
>
B．>>
C．>>
D．>>
11．我们知道，溶液的酸碱度由pH确定．当pH＞7时，溶液呈碱性；当pH＜7时，溶液呈酸性．若将给定的HCI溶液加水稀释，那么在下列图象中，能反映HCI溶液的pH与所加水的体积（v）的变化关系的是（ ）
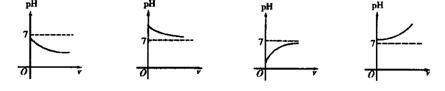
A B C D
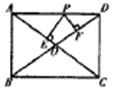12．如图，在矩形ABCD中，AB＝3，AD＝4．P是AD上的动点，PE⊥AC于E，PF⊥BD于F．则PE＋PF的值为（ ）
A．
B．2 C．
D．
二、填空:本大题共8小题；每小题4分，共32分．把答案填写在题中横线上．
13．函数y=
中自变量x的取值范围是
。
14．已知函数：（1）图象不经过第二象限；（2）图象经过（2，-5），请你写出一个同时满足（1）和（2）的函数关系式：________________________________________________.
15．某校去年对实验器材的投资为2万元，预计今明两年的投资总额为8万元，若设该校这两年在实验器材投资上的平均增长率为x，则可列方程：__________．
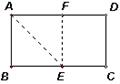16．如图，一张矩形纸片，要折叠出一个最大的正方形.小明
把矩形的一个角沿折痕AE翻折上去，使AB和AD边上的AF
重合，则四边形ABEF就是一个最大的正方形.他的判定方法是
_____________________________________________________.
17．如图是2002年6月份的日历，现有一矩形在日历任意框出4个数
，请用一个等式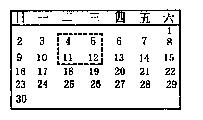
表示a、b、c、d之间的关系：__________．
18、为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若测得PA=5cm，则铁环的半径是
cm
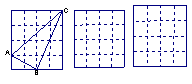19．正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等。
20．.张明同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时，其影长为1.2米，当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子在墙上.经测量，地面部分影长为6.4米，墙上影长为1.4米，那么这棵大树高约________米.
三、解答题：（本题共8个小题，共82分）
21．（本小题满分8分）
计算：
－sin60°＋（－
）0－
．
22（本题满分8分）
在菱形ABCD中，E、F分别在CD、BC上，且CE=CF，求证：AE=AF
23．（本题满分8分）某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
（1）求这15位营销人员该月销售量的平均数、中位数和众数；
（2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由．
24（本题10分）已知关于x的一元二次方程 ax2+x—a=0 ( a≠0 )
（1） 求证：对于任意非零实数a，该方程恒有两个异号的实数根;
（2） 设x1、 x2是该方程的两个根，若∣x1∣+ ∣x2∣=4，求a的值。
25．（本题满分10分）某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下讨论：
甲同学：这种多边形不一定是正多边形，如圆内接矩形；
乙同学：我发现边数是6时，它也不一定是正多边形，如图一，△ABC是正三角形，
＝
＝
，可以证明六边形ADBECF的各内角相等，但它未必是正六边形；
丙同学：我能证明，边数是5时，它是正多边形，我想，边数是7时，它可能也是正多边形．
……
（1）请你说明乙同学构造的六边形各内角相等．
（2）请你证明，各内角都相等的圆内接七边形ABCDEFG（如图二）是正七边形（不必写已知、求证）．
（3）根据以上探索过程，提出你的猜想（不必证明）．
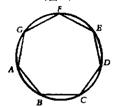
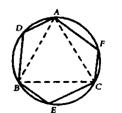
(图一) （图二）
26．（本题12分）某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。
| 印数a (单位：千册) | 1≤a＜5 | 5≤a＜10 |
| 彩色 (单位：元/张) | 2．2 | 2．0 |
| 黑白（单位：元/张） | 0．7 | 0．6 |
（1）印制这批纪念册的制版费为 元；（2）若印制2千册，则共需多少费用？
（3）如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围。（精确到0.01千册）
27．（本题12分） 如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0），（3，4）。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥AC，交AC于P，连结MP。已知动点运动了x秒。
（1）P点的坐标为（ ， ）；（用含x的代数式表示）
（2）试求 ⊿MPA面积的最大值，并求此时x的值。
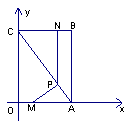（3）请你探索：当x为何值时，⊿MPA是一个等腰三角形？
你发现了几种情况？写出你的研究成果。
28. （本题14分）已知：如图，点A在y轴上，⊙A与x轴交于B、C两点，与y轴交于点D（0，3）和点
（1）求经过B、E、C三点的二次函数的解析式；
（2）若经过第一、二、三象限的一动直线切⊙A于点P（s，t），与x轴交于点M，连结PA并延长与⊙A交于点Q，设Q点的纵坐标为y，求y关于t的函数关系式，并观察图形写出自变量t的取值范围；
（3）在（2）的条件下，当y＝0时，求切线PM的解析式，并借助函数图象，求出（1）中抛物线在切线PM下方的点的横坐标x的取值范围。
