下学期九年级数学总复习试题(一)
一、选择题：
1、下列运算正确的有（ ）个
① x3+x3 = 2x6 ② x6÷x2 = x3 ③ (-3x3)2 = 3x6 ④ x2×x = x3⑤ (3x3)2 = 9x6 ⑥ (-)0 = 0
⑦ (-1)-1 = 1-⑧ = 3-Л A、2 B、 4 C、 5 D、6
2、在毕业联欢会上，主持人准备了一些纸片，上面共有游戏活动6项、文艺表演4项，小王和小李依次各抽一张纸条，则小王抽到游戏活动的机会和小李抽到文艺表演的机会分别是（ ）
A、， B 、， C 、 ， D、，
3、已知A，B，C，D为同一平面内的四点，给出以下四个条件：①AB∥CD②BC∥AD③AB = CD④BC = AD 从中任选两个，不能使之为 的选法是（ ） A、①② B、①③
C、②③ D、③④
4、某计算装置有一数据入口A和一运算结果输出口B，如表是小明同学输入的一些数据及所得运算结果。若小明输入数据2005，那么输出的结果应是（ ）
A、 B、2+1 C、45 D、
| A | 0 | 3 | 8 | 15 | 24 | 35 | --- |
| B | 1 | 2 | 3 | 4 | 5 | 6 | --- |
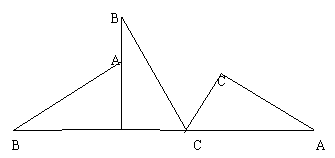5、如图，直角三角板ABC的∠B= 300，
∠C = 900 ，AC = 1。若将三角板ABC
沿水平方向按图所示的方向翻滚，则点
B从开始至结束所走过的路径长度为（ ）
A、 +2 B 3+
C (+)Л D (+2)Л
6、若x2+mx-18 = (x-9)(x+n)对一切实数x都成立，则mn的值是（ ）
A、2 B、-5 C、-7 D、-14
7、若0＜x＜10，则点P（m-10，m）所在的象限是（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
8、同学用计算器算得：①293 = 24389 ②sin350 = 0. ③使tanα= 5的锐角α = 78.0 ④ = 7.，根据你的估算，其中错误的是（ ）A ① B ② C ③ D ④
9、在一次课外活动中，几个同学分别提出以下命题：甲：“一个三角形按比例扩大或缩小后，其三内角分别与原来相等”；乙：“45名同学全部面向主席台排成一行，每次有且只有6名同学齐向后转，无论经过多少次变换，45名同学始终不能全部背向主席台”；丙：“一次校庆活动中，某年级36个同学来自6个班，每班6人，始终不能将他们排成一个方阵，使得每行每列的6个同学来自6个不同的班”；丁：“三边长都是整数的直角三角形，其面积不可能是整数的平方”，其中所提命题为假命题的同学为（ ）
A、甲 B、乙 C、丙 D、丁
10、向高层建筑的圆柱形水箱注水，水对水箱底部的压强P与水深h的函数关系的图象是（ ）（H为最大水深）
 |
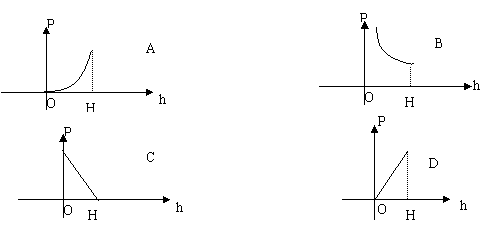二、填空题：
11、计算：-32+（）-1 = 。 12、分解因式：x2+y2-4-2xy = .
13、已知：2+= 22×，3+= 32×，4+= 42×，……，若10+= 102×,则a+b = .
14、已知m,n是方程x2-3x-7 = 0的两个实数根，则m2+mn+3n的值为
。
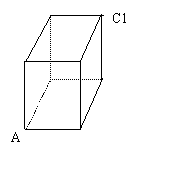
15、如图，长方体高3cm，底面是正方形，
边长为2cm，现有一虫子从A出发，沿长方体表面爬行到C1处，
则虫子爬行的最短路程是 cm.
16、已知抛物线L：y = ax2+bx+c（其中a,b,c均不为0）的顶点为P（-,），
与y轴的交点为M（0，c）如果称直线PM为抛物线L的伴随直线；以M为顶点对称轴是y轴且过点P的抛物线为L的伴随抛物线。则写出抛物线y = 2x2-4x+1的伴随直线的解析式 ，伴随抛物线的解析式是 。
三、解答题：
17、是否存在实数m，使关于x的一元二次方程(m+15)x2-(3m+5)x+12 = 0的两实数根分别是一个直角三角形两锐角的正弦？如果存在，求出m的值；如果不存在，请说明理由。
18、如图，某森林保护区是以A为中心、150km为半径的一个圆形区域。在距中心A点240km的正西方向有一座城市B，在城市B的北偏东600方向500km处有城市C。现计划在BC两城市之间修一条高速公路（既线段BC），计划修筑的这条高速公路是否会穿越森林保护区？若会，请求出森林保护区内的公路长；若不会，请说明理由。
 | |||
 | |||
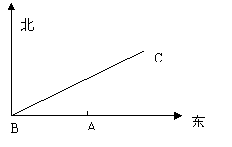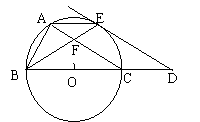
19、如图、点A在⊙O上，⊙O的直径BC的长为2，∠ABC的平分线交⊙O于点E，交AC于点F，过点E作⊙O的切线，交BC的延长线于点D，连结CE。
⑴求证：AC∥ED； ⑵若AB = AE，求AF的长； ⑶若点A由点B出发，在⊙O的圆周上运动，当点A在什么位置时，AE与BD互相平行。
20、某高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技产品，并一次性投入了资金1500万元做生产设备等多方面的准备工作。已知生产每件产品另需成本费40元，并在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件。设销售单价为x（元），年销售量为y（万件），年获利（年获利 = 年销售额-生产成本-投资）为z（万元）
⑴试写出y与x之间的函数关系式（不必写出x的取值范围）
⑵试写出z与x之间的函数关系式（不必写出x的取值范围）
⑶计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别为多少万件？
⑷公司计划：在第一年按年获利最大确定的销售单价进行销售，到第二年底总获利不低于1130万元，请你利用函数的大致图象说明，第二年的销售单价x（元）应确定在什么范围内？
21、已知在直角坐标系中，点M（，0）为Rt△OED斜边上的中点，O为坐标原点，点E在x轴上，点D在第一象限内，∠ODE = 900，过D作AB⊥DM交x轴的负半轴于A点，交y轴的正半轴于B点，且sin∠OAB = ，求D点的坐标。
22、某公司甲、乙两个部门到集市购买苹果，苹果的价格如下：
| 购买苹果的重量 | 不超过30kg | 30kg以上但不超过50kg | 30kg以上 |
| 每千克的价格 | 3元 | 2.5元 | 2元 |
由于某种原因，甲部门分两次购买苹果（第二次多于第一次），共购入70千克，支出189元；乙部门则一次性购买苹果70千克。
⑴同样购买70千克苹果，甲、乙两部门的购买方式支出的费用是否相等？
⑵甲部门第一次购买的苹果是多少千克？
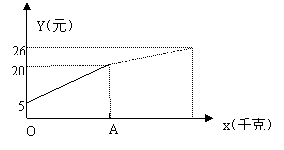
23、一农民有若干千克自产的土豆进城，为了方便，他带了一些零钱备用。刚开始，他按市场价售出一部分，又降价出售，他手中持有的钱（元）数（含备用零钱）与售出的土豆（千克）数的关系如图所示，结合图象回答下列问题：
① 降价前他出售的土豆的单价是多少？
② 降价后他按每千克0.4元将剩下的土豆售完。这时他手中的钱（含备用钱）是26元，他一共带了土豆多少千克？
③ 直接写出他手中持有的钱数y（元）与售出的土豆数x（千克）之间的函数关系式。
 |
24、（本小题满分9分）
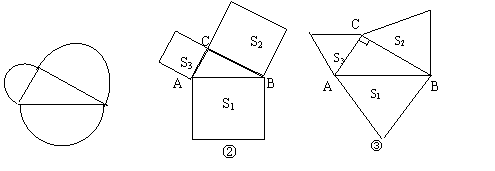
如图①，分别以直角三角形ABC三角形三边为直径向外作三个半圆，其面积分别用S1、、S2、S3表示，则不难证明S1 = S2+S3。
⑴如图②分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1、、S2、3表示，那么S1、、S2、S3之间有什么关系？（不必证明）
⑵如图，分别以直角三角形ABC三边为边向外作在三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1、、S2、S3之间的关系并加以证明；
⑶若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1、、S2、S3表示，为使S1、、S2、S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件？证明你的结论；
⑷类比（1）、（2）、（3）的结论，请你总结一个更具有一般意义的结论。
C
S3 S2
A S1 B
①