中考数学模拟题(四)
一,选择题(每小题4分,共计32分) 总分
1,已知a、b为实数,下列个式中一定为正值的是( )
A,![]() B,
B,![]() C,
C,![]() D,
D,![]()
2,在下列各组根式中,是同类二次根式的是( )
A,![]() 和
和![]() B,
B,![]() 和
和![]()
![]() C,
C,![]() 和
和![]() D,
D,![]()
| A |
 3,如图,菱形花坛ABCD的边长为6㎝,∠B=60°,其中右两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为(
)
3,如图,菱形花坛ABCD的边长为6㎝,∠B=60°,其中右两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为(
)
| D |
| C |
 A,
A,![]() ㎝ B,20㎝ C,22㎝ D,24㎝ B
㎝ B,20㎝ C,22㎝ D,24㎝ B
4,将一长方形纸片按如图的方式折叠,BC、BD为折痕,则
| D |
 ∠CBD的度数为( )A,60° B,75° C,90° D,95°
∠CBD的度数为( )A,60° B,75° C,90° D,95°
| A |

![]() 5,一根1米长的绳子,第一次剪去一半,第二次剪去剩下
5,一根1米长的绳子,第一次剪去一半,第二次剪去剩下
| C A |
| E |
 的一半,如此剪下去,第六次后剩下的绳子的长度为( )
的一半,如此剪下去,第六次后剩下的绳子的长度为( )
| B |
| E |
A,![]() 米 B,
米 B,![]() 米 C,
米 C,![]() 米 D,
米 D,![]() 米
米

 6,如果x1、x2是方程2x2-4x+1=0的两个根,那么
6,如果x1、x2是方程2x2-4x+1=0的两个根,那么![]() 的值为(
)
的值为(
)
![]() A,
A,![]() B,3 C,4 D,6
B,3 C,4 D,6
7,若a、b、s、r都是正数,则式子![]() 可变形为(
) (8题)
可变形为(
) (8题)
A,a=![]() B,b=
B,b=![]() C,b=
C,b=![]() D,
D,![]()
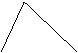
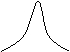
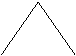
8,如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上任一点,过P作EF⊥AC,与平行四边形的两条边分别交于点E、F,设BP=x,EF=y,则能反映y与x之间关系的函数图象为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 4
4
4
4
4
4
4
4
A B C D
![]()
![]()
![]()
![]() O 3 6 O 3 6 O 2 6 O 3
O 3 6 O 3 6 O 2 6 O 3
二,填空题(每小题3分,共计18分)
9,一种细菌的半径是0.00004米,用科学记数法可把它表示为 米。
![]() 10,不等式组 2x-1>10
10,不等式组 2x-1>10
x+8<4x-1的解集为 。
11,有一捆粗细均匀的电线,现在要确定其长度的值,从中先取出1米长的电线,称出它的质量为a,再称其余电线的总质量为b,则这捆电线的总长度是 米。
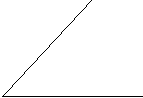 12,多项式x2+px+12可分解为两个一次因式的积,整数p的值可以是 。(只写一个)
12,多项式x2+px+12可分解为两个一次因式的积,整数p的值可以是 。(只写一个)
 13,如图,AB、AC与⊙O相切于B、C,∠A=50°, C
13,如图,AB、AC与⊙O相切于B、C,∠A=50°, C
点P是圆上异于B、C的一动点,则∠BPC的度数是 。
14,△ABC中AB=AC,∠A=36°,∠ABC的 ·O
平分线交AC于D,则BC2+AB·BC-AB2= 。
三,解答题(共计70分) A B
![]()
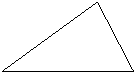 15,(6分)如图,D为△ABC边上一点,∠CAD=∠B,若AD=6,AB=8BD=7,求DC的长。
A
15,(6分)如图,D为△ABC边上一点,∠CAD=∠B,若AD=6,AB=8BD=7,求DC的长。
A
B D C
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
16,(7分)声音在空气中传播的速度y(米/秒)(简称音速)是气温x(℃)的一次函数,下表列出一组不同气温时的音速:
(1)求y与x之间的函数关系式;
(2)气温x=22℃时,某人看到烟
花燃放5秒后才听到声响,那么此人与燃放的烟花所在地约相距多远?
![]() 17,(7分)如图,已知一灯塔A的周围7海里的范围内有暗礁,一艘渔轮在B处测得灯塔A在北偏东60°的方向,向正东航行8海里到达C处后,又测得该灯塔在北偏东30°的方向,渔轮如不改变方向,继续向正东航行,有没有触礁危险?请通过计算说明理由。
17,(7分)如图,已知一灯塔A的周围7海里的范围内有暗礁,一艘渔轮在B处测得灯塔A在北偏东60°的方向,向正东航行8海里到达C处后,又测得该灯塔在北偏东30°的方向,渔轮如不改变方向,继续向正东航行,有没有触礁危险?请通过计算说明理由。
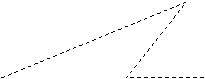 A
A
| 60° |
| 30° |
![]()
![]() 北
北
B C 东
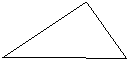 18,(7分)如图,已知△ABC中,∠A=2∠B,CD是∠ACB的平分线。 A
18,(7分)如图,已知△ABC中,∠A=2∠B,CD是∠ACB的平分线。 A
![]() 求证:BC=AD+AC。
D
求证:BC=AD+AC。
D
B C
19,(7分)某公司欲聘请一位员工,三位应聘者A、B、C的原始评分如下表。
|
应聘人 | 仪表 | 工作经验 | 电脑操作 | 社交能力 | 工作效率 |
| A | 4 | 5 | 5 | 3 | 3 |
| B | 4 | 3 | 3 | 4 | 4 |
| C | 3 | 3 | 4 | 4 | 5 |
(1)如果按五项原始评分的平均数评分,谁将被聘用?
(2)如果按仪表、工作经验、电脑操作、社交能力、工作效率的原始评分分别占10%、15%、20%、25%、30%综合评分,谁将被聘用?
20,(7分)某城市为了鼓励节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨部分,按0.45元/吨收费;超过10吨而不超过20吨部分,按0.80元/吨收费;超过20吨部分,按1.5元/吨收费,现已知李老师家六月份缴水费14元,问李老师家六月份用水多少吨?
21,(9分)已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h。“若点P在一边BC上(如图1),此时h3=0,可得结论:h1+h2+h3=h”。请直接应用上述信息解决下列问题:当点P在△ABC内(如图2)、点P在△ABC外(如图3)这两种情况时,上述结论是否成立?若成立,请给予证明;若不成立,h1、h2、h3与h之间又有怎样的关系,请写出你的猜想,不需证明。

![]()
![]()

![]()
 A
A A
A
A A
![]()
![]() D
D
D
D

![]()
![]()
![]()
![]() E
E
D
E
E
E
D
E
![]()
![]() B
C B
C B
F
C
B
C B
C B
F
C
M P M P M P
图1 图2 图3
22,(10分)已知⊙O1与⊙O2外切,⊙O1的半径R=2,设⊙O2的半径是r。
(1)如果⊙O1 与⊙O2的圆心距d=4,求r的值;
(2)如果⊙O1、⊙O2的公切线中有两条互相垂直,并且r≤R,求r的值。
23,(10分)如图已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角。
(1)若二次函数y=![]() 的图象经过A、B两点,求它的解析式;
的图象经过A、B两点,求它的解析式;
(2)点C(1)中求出的二次函数的图象上吗?请说明理由。
![]() y
y
| C |
 |
α |
| β |
![]() O A
B x
O A
B x