九年级数学模拟试题（二）A
（时间：120分钟 满分：150分）
第一部分 选择题（共36分）
一、选择题：（下列各题所给答案中，只有一个答案是正确的，每小题3分，共36分）
1、—2的绝对值是 （ ）
A、—2 B、2 C、
D、—
2、下列各式的计算结果是a6的是 ( )
A、（-a3）2 B、a3+a3 C、a12÷a2 D、a2·a3
3、润扬长江公路大桥的建设创造了多项国内第一，综合体现了目前我国公路桥梁建设的最高水平，据统计其混凝土浇灌量为m3，用科学记数法表示 （ ）
A、1.06×106m3 B、1.06×105m3 C、1.06×104m3 D、1.06×105m3
4、⊙O的半径为4㎝，⊙P的半径为1㎝，若⊙O与⊙P内切，则O、P两点的距离（ ）
A、等于3㎝ B、等于5㎝ C、等于3㎝或5㎝ D、介于3㎝与5㎝之间
5、红星学校准备开办一些学生课外活动的兴趣班，结果反应热烈。各种班的计划招生人数和报名人数，列前三位的如下表所示
| 班 | 计算机 | 奥数 | 英语口语 |
| 计划人数 | 100 | 90 | 60 |
| 班 | 计算机 | 英语口语 | 音乐艺术 |
| 报名人数 | 280 | 250 | 200 |
若计划招生人数和报名人数的比值越大，表示学校开设该兴趣班相对学生需要的满足度就越高，那么根据以上数据，满足程度最高的兴趣班是 （ ）
A、计算机班 B、奥数班 C、英语口语 D、音乐艺术班
6、下列事件中是必然事件的是 （ ）
A、买体育彩票一定中奖 B、十五的月亮是圆的
C、明天是晴天 D、抛出的篮球会下落
7、一张桌子上摆放着苦十个碟子，从三个方向上看在眼里，三种视图如下图所示，则这张桌子上共有碟子为 （ ）
A、6个 B、8个 C、12个 D、17个
 |
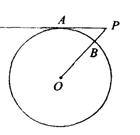8、如图，P为⊙○外一点，PA为⊙○的切线，OP交⊙○于B，设PA=x， ⊙○的半经为y，PB=2，则y与x的函数关系式为
（） A.
B.
C.
D.
9、抛物线y=ax2+2ax+a2+2的一部分如图所示，那么该抛 物线在y轴右侧与x轴交点的坐标是 ( )
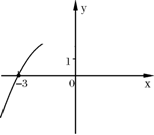A．（，0） B．（1， 0）
C．（2， 0） D．（3， 0）
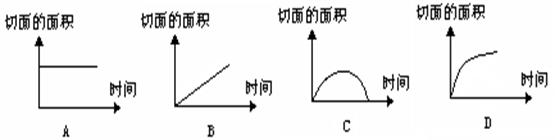
10.下面哪副图能大致表示切土豆（一刀）的过程 ( )
 |
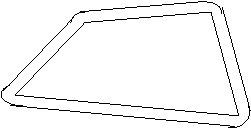
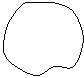11、不规则的图形的面积可以用正方形纸覆盖来近似地测量，用不规则图形完全覆盖住的方格数与不规则图形接触到的方格数的平均数来近似地计算不规则图形的面积，请你实际计算一下如图所示的不规则图形的面积，它的面积约（ ）
A 20平方单位
B 20.5平方单位
C 22平方单位
| |
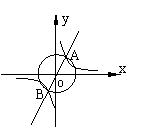12、如图,直线y=kx与双曲线y=
相交于A,B,以AB为为直径的圆的面积为S,则S的值不可能是
( )
A.π B.2π
C.3π D.4π
第二部分 非选择题（共114分）
二、填空题：（每小题3分，共24分）
13、已知函数y=
则自变量x的取值范围是
。
14、已知x=2,则
=
。
15、如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝30°，则∠CAD等于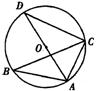
。
16、如图是一张简易活动餐桌,现测得OA=OB=30cm，OC=OD=50cm，现要求桌面离地面的高度为40cm，那么两条桌腿的张角∠COD的大小应为 。
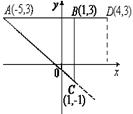
17、已知A、B、C、D点的坐标如图所示, 
是图中两条虚线的交点, 若△ABC 和△ADE相似, 则点的坐标是______________。
 |
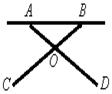
第15题 第16题 第17题 第19题
18、杉杉打火机厂生产某种型号的打火机，每只的成本为2元，毛利率为25%。工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，则这种打火机每只成本降低了 元。（精确到0.01元，毛利率=
×100%）
19、如图有一不规则四边形ABCD的住宅小区，其周长2000米，现要在它周围造一条环形小道，其路宽3米，转弯处是与直路的外沿相切的圆弧路线，则所造小路的面积
为 米２（保留π）
20、 观察下列由棱长为1的小立方体摆成的图形：
如图①中：共有1个小立方体，其中1个看得见，0个看不见；
如图②中：共有8个小立方体，其中7个看得见，1个看不见；
如图③中：共有27个小立方体，其中19个看得见，8个看不见；……
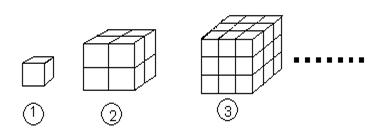则第⑨个图中，看不见的小立方体有 个 ；
三、解答题：
21、(本题满分8分)
－1（3－
）0＋sin450·tan600-
÷
22、(本题满分8)
解不等式组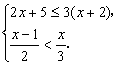
并写出不等式组的整数解
23、解直角三角形的应用（本题满分8分）
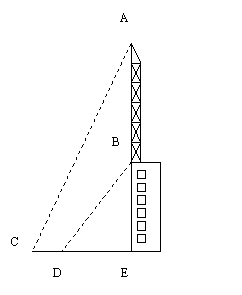
已知：如图，楼顶有一根天线，为了测量楼的高度，在地面上取成一条直线的三点E、D、C，在点C处测得天线顶端A的仰角为60°，从点C走到点D，CD＝6米，从点D处测得天线下端B的仰角为45°．又知A、B、E在一条线上，AB＝25米，求楼高BE．
  |
24、(本题满分10分)
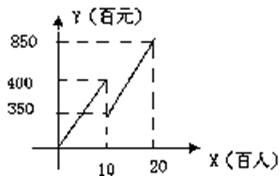
一次时装表演会预算中票价定为每张100元，容纳观众人数不超过2000人，毛利润y（百元）关于观众人数x（百人）之间的函数图像如图所示，当观众人数超过1000人时，表演会组织者需向保险公司缴纳定额平安保险费5000元（不列入成本费用），请解答下列问题：
（1）求当观众人数不超过1000人时，毛利润y关于观众人数x的函数解析式和成本费用S（百元）关于观众人数x的函数解析式.
（2）若要使这次表演会获得36000元的毛利润，那么需售出多少张门票？需支付成本费用多少元？
 |
25、(本题满分10分)
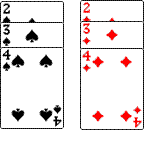
现有一项资助贫困生的公益活动由你来主持，每位参与者需交赞助费10元，活动规则如下：如图是从一副扑克牌中取出的两组牌，分别是黑桃2、3、4和方块2、3、4，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面数字之和等于8则获得一等奖，奖金20元；数字之和为7则获得二等奖，奖金10元；数字之和为6则获得三等奖，奖金为5元；其余均不得奖。此次活动所集到的赞助费除支付获奖人员的奖金外，其余全部用于资助贫困生的学习和生活。
（1） 分别求出此次活动中获得一等奖、二等奖、三等奖的概率。
（2） 若此次活动有3000人参加，活动结束后有多少元赞助于资助贫困生。
 |
26、（本题满分8分）
已知抛物线
的顶点A在直线
上.
(1)求抛物线顶点A的坐标；
(2)求抛物线与x轴两交点B、C的坐标；
(3) 求∠ABC的余切值.
27、(本题满分12分）
2006年泰州市春季房交会期间，某公司对参加房交会的消费者进行了随机问卷调查，共发放了500份调查问卷，并全部收回，根据调查问卷将消费者年收入的情况整理后制成表格如下：
| 年收入（万元） | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数（人） | 100 | 250 | 100 | 35 | 15 |
将消费者打算购买住房面积情况整理后，作出部分频数分布直方图（如图）
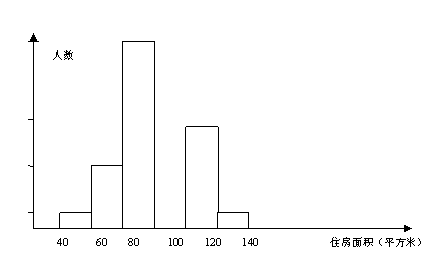
注：每组包含最小值不包括最大值，且住房的面积取整数
请你根据以上信息，回答下列问题
（1）根据表格可得，被调查的消费者平均年收入为 万元；被调查的消费者收入的中位数是 万元；在平均数、中位数这两个数中 更能反映被调查消费者年收入的一般水平。
（2）根据频数分布直方图可得，打算购买100～120平方米房子的人数为 人；打算购买住房面积小于100平方米的消费者人数占被调查消费者人数的百分数是 。
（3）在图中补全这个频数分布直方图。
28、(本题满分12分)
小明家打算建一个苗圃，苗圃的两边靠墙（这两堵墙互相垂直），另外的部分用30米长的篱笆围成. 小明的爸爸提出一个问题：怎样围才能使苗圃的面积尽可能地大？小明思考后，设计了以下三种方案：
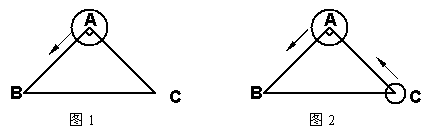
方案一：围成斜边为30米的等腰直角三角形（如图1）；
方案二：围成边长为15米的正方形（如图2）；
方案三：围成直角梯形，其中∠BCD＝120°（如图3）.
解答下列问题：
⑴ 分别计算方案一、方案二中苗圃的面积S1，S2，并比较S1，S2的大小；
⑵ 设方案三中CD的长为x米，苗圃的面积为S3平方米，求S3与x之间的函数关系式，并求出S3的最大值；
⑶ 请你设计一种方案，使围成的苗圃面积比上述三个方案中的任何一个面积都大.（要求在图4中画出草图，标上必要的数据，并通过计算加以说明）
 |
29、（本题满分14分）
如图1，在Rt⊿ABC中，∠A＝90o，AB＝AC，BC＝8
㎝，大圆的圆心在A点，半径为2㎝，大圆以1cm / s的速度移动（圆心从A点出发，沿A—B—C—A方向移动，圆心始终在Rt⊿ABC边上），设运动时间为t（s）．
（1）当大圆与AC边相切时，求t的值；
（2）如果一个小圆的圆心在C点，半径为1㎝，它与大圆同时出发，以2cm / s的速度沿C—A—B—C方向移动，当一个圆的圆心到达其出发点时，另一个圆也停止移动（如图2）.
①当两圆相切时，它们的圆心都同时在（ ）
A. AC边上 B. AB边上 C. BC边上 D. AB和BC边上
②当两圆相切时，求t的值．