九年级数学上中段模拟试题
班级: 姓名: 座号: 成绩:
一.选择题:(每题3分,共15分)
1.下列数据为长度的三条线段可以构成直角三角形的是（ ）
A.3、5、6 B. 2、3、4
C. 6、7、9 D.9、12、15
2.正方形具有而菱形不具有的性质是( )。
A.内角和360° B.四个角都是直角
C.两组对边分别相等 D.对角线平分对角
3.一件产品原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低成本（ ）
A.8.5% B.9% C.9.5% D.10%
4.M（
、N（
、P（
）三点都在函数
（
＜0 的图象上，则（ ）．
A.
＞
＞
B.＞＞ C.＞＞ D.＞＞
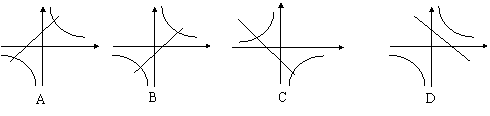5.在同一坐标系中，函数和
的图像大致是 （ ）
二.填空题:(每题3分,共30分)
6.直角三角形两直角边分别是5cm和12cm，则斜边长是 ，斜边上的高是 cm.
7．已知方程
的一个根是-5，求它的另一个根是
，= 。
8．方程
的根是
9. 双曲线
经过点（2 ，―3），则k =
；
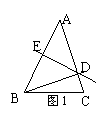
10.已知：如图1，△ABC中，AB=AC，∠A=40º，AB的中垂线交AC于点D，交AB于点E，则∠C= ，∠DBC= .
11．菱形的两对角线长之比为2
: 3 ，面积为
，则两条对角线的长分别为__________；
12.近视眼镜的度数
（度）与焦距
（米）成反比例，已知400度的近视眼镜镜片的焦距为0.25米，则眼镜的度数与焦距之间的函数关系式是
.
13.直线y＝ax＋b（a≠0）不经过第二象限，则双曲线y＝
一定分布在第 象限。
14．若四边形的对角线相等,则顺次连结这个四边形各边中点所得的四边形是 。
15．如图2，以正方形ABCD的对角线AC为一边，延长AB到E，使AE = AC，以AE为一边作菱形AEFC，若菱形的面积为
，则正方形边长
三.解答题:(共55分)
16.解方程:.(1)
(4分)
(2)
(4分)
17.画出下图中物体的三种视图。(4分)
18．(5分)已知，如图3，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.（1）请你在图3中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.
 |
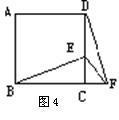
19.(6分)如图4，正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE=CF.
（1）求证：△BCE≌△DCF；（2）若∠BEC=600，求∠EFD的度数.
 |
20.(6分)求证：连接矩形各边中点得到的四边形为菱形。
21.（6分）如图，在
中，
，点
从点
开始沿
边向点
以
的速度匀速移动，同时另一点
由点开始以
的速度沿着
匀速移动，几秒后，
的面积等于
？
22.(6分)某商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，如果每件提价1元出售，其销售量就减少20件。现在要获利12000元，且销售成本不超过24000元，问这种服装销售单价确定多少为宜？这时应进多少服装？
23．(6分)如图，A为双曲线上一点，过A作AC⊥x轴，垂足为C，且S△AOC=2．
(1) 求该反比例函数解析式；
(2) 若点(-1,y1),(-3,y2)在双曲线上，试比较y1、 y2的大小．
24.(8分)如图13－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
（1）如图13－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
（2）若三角尺GEF旋转到如图13－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．
附加题:(10分)如图，Rt△ABO的顶点A是双曲线与直线
在第二象限的交点，AB⊥轴于B且S△ABO=
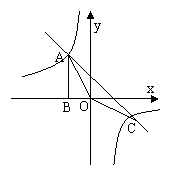（1）求这两个函数的解析式。（2）求直线与双曲线的两个交点A，C的坐标。
（3）在x轴上是否存在点P，使△AOP为等腰三角形？
若存在，符合条件的点P有多少个，若不存在，请说明理由。