九年级数学试卷2
（本卷满分150分，考试时间120分钟）
第 Ⅰ 卷（选择题，共27分）
友情提醒：第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上的答案标号涂黑.
一、选择题：本大题共9小题，每小题3分，共27分.
1．二次根式
的值是
( )
A．-3 B．3或-3 C．3 D．9
2．下列图形中，是中心对称图形的是-----------------------------------（ ）
A.菱形 B.等腰梯形 C.等边三角形 D.等腰直角三角形
3．在函数y=
中，自变量x的取值范围是
( )
A．x≥3 B．x≤3 C．x＞3 D．x＜3
4．下列计算正确的是 （ ）
A．
B．
C.2+
D．
5．下列各式中，与
是同类二次根式的是
（ ）
A．
B．24 C．
D．
6．下列二次根式2
，
，
中,最简的二次根式的个数是 ( )
A.2 B.3 C.4 D.5
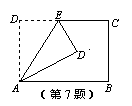7．如图，将矩形ABCD沿AE折叠，若∠BAD′＝30°，
则∠AED′等于 ( )
A．30° B．45°
C．60° D．75°
8．式子
成立的条件是
（ ）
A．a≥2 B.a≤1 C.1≤a≤2 D.1＜a≤2
9．顺次连结等腰梯形四边中点得到一个四边形，再顺次连结所得四边形四边的中点得到的图形是 ( )
A.等腰梯形 B.直角梯形 C. 菱形 D.矩形
第 Ⅱ 卷 （非选择题，共123分）
二、填空题：本大题共7小题，每小题3分，共21分.
10．实数范围内分解因式:2x2－4= ．
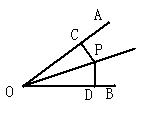
11．如图，P是∠AOB的平分线上的一点，PC⊥OA，垂足为C，PD⊥OB，垂足为D，写出图中一组相等的线段： （只需写出一组即可）．
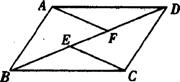12．如图，在□ABCD中，E，F是对角线BD上的两点，要使△ADF≌△CBE，还需添加一个条件为
(只需添加一个条件).
（第11题） （第12题）
13.在四边形ABCD中,AB∥CD,AD=BC,则四边形ABCD的形状是 .
14．若1≤
≤2，化简
=
.
15．若以3cm,5cm为底,6cm,xcm为腰画梯形,则x的取值范围是 .
16．观察下列各式：
；
根据上述各式反映的规律，写出用n（n为任意的自然数，且n≥2）表示的等式为
.
三、计算或化简: 本大题共5小题，每题6分，共30分.
17．
18． 
+
19． 2a
（a≥0，b≥0）
20．最简的二次根式
与
是同类二次根式,求a的值.
21．已知:实数x、y满足y=
,求
的值.
四、解答下列各题：本大题共4小题，每题7分，共28分.
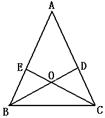
22．如图, △ABC中, D、E分别是AC、AB上的点, BD与CE交于点O. 给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD.
⑴ 上述三个条件中,可判定△ABC是等腰三角形的两个条件为 (用序号写
出所有情形)；
⑵ 选择第⑴小题中的一种情形, 证明△ABC是等腰三角形.
23．已知:如图,平行四边形ABCD的对角线AC的平分线与边AD、BC分别相交于E 、F.
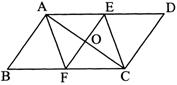求证：四边形AFCE是平行四边形.
24．阅读理解：由 
可以看出,结果中不含二次根式.若两个含有二次根式的代数式相乘,积不含有二次根式,则称这两个代数式互为有理化因式.因此有理化因式在二次根式的化简中有很大的作用.
例 化去
分母中的根号.
解: =
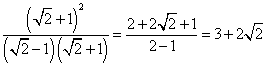
仿照上面的方法,解答下列问题:
（1）化简:
=
;
（2）已知a是的小数部分,求
的值.
25．操作与证明：用一张矩形纸片折等边三角形.
(1)如图①,把矩形纸片ABCD对折后再展开,折痕为EF;
 |  |
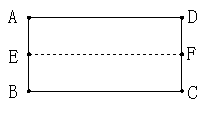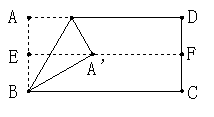图① 图②
(2)如图②, 将点A翻折到EF上的点A’处,且使折痕过点B;
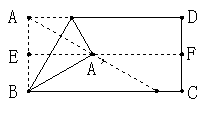(3)如图③,沿A’A折叠,得△A’BA.
△A’BA是等边三角形吗?请说明理由.
图③
五、解答下列各题：本大题共4小题，第26、27题各10分，第29题12分，第30题12分，共44分.
26．如图，在四边形ABCD中，AB=DC，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点.
（1）四边形EGFH是怎样的四边形？请证明你的结论；
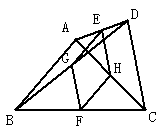（2）连接EF，探求EF与AB的大小关系为
（填“>”、“=”或“<”），并证明你的结论.
27．已知：如图，矩形ABCD中，AB=6cm，AD=8cm，动点F从A点出发，沿AD以4cm/s的速度运动；同时动点E从B点出发，沿对角线BD以5cm/s的速度运动，设运动的时间为ts(t<2).
（1）求证：四边形ABEF为梯形；
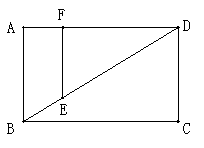（2）当t为何值时，梯形ABEF的面积是△BDC面积的一半.
28．操作与探究：
（1）图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠，使点A与点C重合，DE为折痕。试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)，当满足条件 时，一定能折成组合矩形？
 |
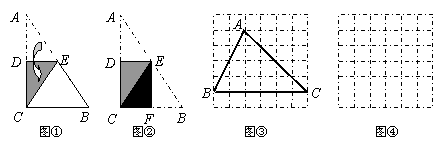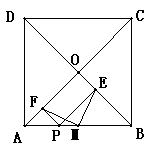
29．已知:正方形ABCD的对角线AC、BD相交于点O，点P是直线AB上一点，PE⊥BD交直
线BD于点E，DF⊥AC交直线AC于点F,M是边AB的中点.
（1）如左图，当点P在边BC上时，①求证: PE＋OE＝AO；②求证:ME=MF;
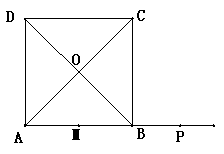
（2）如右图，当点P在线段AB的延长线上时，请你根据题意画出正确的图形，探求
结论: ME=MF是否成立, 并说明理由．
 | |||
 | |||
初三数学试卷参考答案
一、选择
1、C `2、A `3、A``4、B `5、C` 6、A 7、C 8、D 9、D
二、填空：
10、
； 11、略; 12、略； 13、平行四边或等腰梯形; 14、1
15、4<x<8; 16、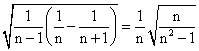
；
三、解答下列问题：
17、
; 18、10+
; 19、
; 20、a=3; 21、
.
四、解答下列问题：
22、(1)①③或②③,—————————2’ (2)证△BEO≌△CDO——————7’
23、证OA=OC,OE=OF————————7’
24、(1)
2——————2’
(2)a=
1<1———————————1’，
原式=
———————————5’
=2———————————————7’;
25、EF垂直平分AB得AA’=A’B—————————3’;
由折叠推出AB=A’B———————7’
五、解答下列问题
26、(1)菱形——————————————————————————1’；
证明：由中位线推出四边相等——————————————5’
(2)AB>EF————————————————————————6’
证明:由△EGF利用EG+GF>EF证得————————————————10’
27、(1)
,
,EF∥AB————————————4’
AD与BD相交于D得AF与BE不平行————————————————5’
（2）t=2-
28、（4）对角线互相垂直(每小题3分)
29、（1）①证PEOF为矩形得结论——————3’,
②连结OM证△AMF≌△OME————————4’
(2)画图1分，证△AMF≌△OME 4分