数学中考模拟测试题

　　 数学中考模拟测试题　

一、选择题：（1～8题每题2分，9～12题每题3分，共28分）

1.★在实数2，sin30°，，– ，3.14，0.…，中有理数的个数是（　 ）

　　A．2个　　　　　　B．3个　　　　 　　C．4个　　 　　　　　D．1个

2.据测算，我国每天因土地沙漠化造成的经济损失约为1.5亿元，若一年按365天计

算，用科学计数法表示我国一年因土地沙漠化造成的经济损失约为　（　 ）

A.元　 B.元　　C.元　D.元

3.下列图形中，是中心对称图形的有　（　　 ）

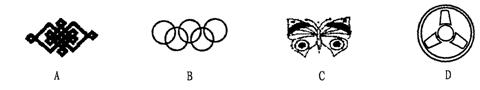
A.1个　　  　　　  C. 2个　　　　 　　　  B.3个　　　　 D.4个

4.抛物线y=x²－6x＋24的顶点坐标是 (　 　)

　　A.( 一6,一6)　　　B.(一6,6)　　　 C.　(6,6)　　　  D.(6, 一6)

5.已知实数x满足x²＋＋x＋－4=0,那么x＋的值为　  (　 　)

A．2或－3　　B．3或－2　　C．1或－6　　D．6或－1

6.★⊙O₁与⊙O₂的半径分别为2cm和3cm，若保持⊙O₁与⊙O₂有公共点，则两圆

圆心距O₁ O₂的取值范围是(　　 )

A.O₁ O₂≤1cm　　B. 1cm≤O₁ O₂≤5cm　 C. 1cm＜O₁ O₂＜5cm　　D.O₁ O₂≥5cm

7.平行四边形ABCD的对角线的交点在坐标原点, 且AD平行于x轴, 若A点坐标为 (－1,2), 则C点的坐标为　（　　）

　　A. (1, －2)　　　　 B. (2, －1 ) 　　　 C. (1, －3) 　　　 D. (2, －3)

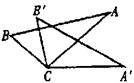
8.★如图，从下列四个条件:（1）BC=B′C，（2）AC=A′C

（3）∠A′CA=∠B′CB,（4）AB=A′B′中任取三个为题设，余下一个作结论，则最多可以构成正确命题的个数是（　　）

A．1个　　　　 　　B．2个　　 

　 C．3个　　　　 　　D．4个

9.如果为实数，且则的取值范围是　　 （　　）

A.任意实数　　 B.负实数　　　 C.　　　　  D.

10.如图，⊙O₁、⊙O₂的外公切线MD、NE交于点A，M、D、N、E为切点，内公切线PQ交AD、AE于点B、C，P、Q为切点，已知AD＝. 那么AB＋BC＋CA等于（　　）

　 Ａ.　　  Ｂ.　　　　 Ｃ.　　 　　　 Ｄ.2

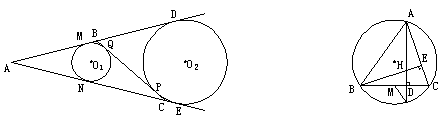
　　　　　　　　　　  (第10题)　　　　　　　　　　　　　 (第11题)　

11.如图，△ABC的高BE、AD交于点H，AD的延长线交△ABC的外接圆于F，M 是 BC的中点，BD＝5， CD＝3，HD＝2，则MF等于（　　）

　 Ａ.　　　　　 Ｂ.　　  　　　Ｃ.4　　　　　　　 Ｄ.

12.下列四个命题中，正确的命题有（　　）

①一个三角形中，至少有一个角不小于60度

②等腰三角形ABC中有两边长分别为3和4，则这个等腰三角形的周长为10或11

③相似三角形周长的比等于对应高的比

④用边长相等的正五边形和正六边形的组合能镶嵌成一个平面

A. 1个　　　　　　　 B.2个　　　　　　  C. 3个　　　　　　  D.4个

二、填空题（每题3分，共24分）www.1230.org 初中数学资源网 收集整理

13.在函数y= ＋的表达式中，自变量x的取值范围是_________.

14.已知一组数据：x,25,20,22,23,24,23,21,22；它们的中位数与众数是同一个数，则x的值为____________.

15.将对角线长分别为4㎝和8㎝的菱形改为一个面积不变的正方形，则正方形的边长为　　　　　　 　　　　 ㎝.

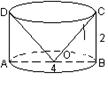16.如图是一口直径AB为4米，深BC为2米的圆柱形养蛙池，小青蛙　　　　　　  们晚上经常坐在池底中心O观赏月亮，则它们看见月亮的最大视角

∠COD= 　　　度，（不考虑青蛙的身高）；

17.★半径是6，圆心角为120°的扇形是某圆锥的侧面展开图，这个

圆锥的底面半径为　　　　　 .

18.已知两圆相交最多有2交点,三个圆相交最多有6个交点,则n个圆相交最多有____________个交点.(用n的代数式表示)

19.★已知：⊙O的半径OA=1，弦AB、AC的长，，则的度数为___________________

20.如图，把△ABC绕C点顺时针旋转35°得△A＇B＇C,

此时恰好A＇B＇⊥AC，则∠A =____________度．

三、解答题

22.⑴★（5分）

⑵（5分）化简：;

23.(7分）已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.

24.（7分）把矩形纸片OABC放人直角坐标系中，使OA、OC分别落在x轴和y轴的正半轴上．

（1）将纸片OAB C折叠，使点A与C重合，用直尺和圆规在原图上作出折叠后的

图形，并在图中标明折叠后点B的对应点B’.（不写作法，保留作图痕迹）

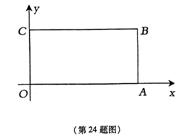（2）在矩形OABC中，连结AC，且AC=2，tan∠OAC=，求A、C两点的坐标；并求（1）中折痕的长

25. （8分）关于的方程，是否存在负数，使方程的两个实数根的倒数和等于４？ 若存在，求出满足条件的的值；若不存在，说明理由。

26. （8分）如图，正方形ABCD的一边AB在x轴正半轴上，点C坐标是 (3，2) ，将直线OD沿x轴正方向平移m个单位。

（1）如果直线OD在移动过程中与边CD有交点，试问m的取值范围，并用m的代数式表示交点坐标；

（2）若将OD在移动过程中扫过正方形的面积记为S，当s=时，求m的值。

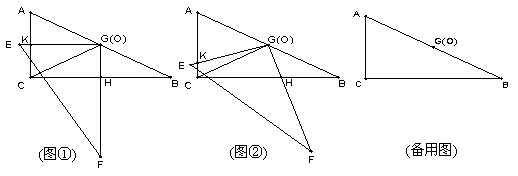
27. （8分）把两个全等的直角三角板ABC和EFG叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，其中∠B＝∠F＝30°，斜边AB和EF长均为4．

(1)当 EG⊥AC于点K，GF⊥BC于点H时（如图①），求GH：GK的值

(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转，旋转角α满足条件：0°＜α<30°（如图②），EG交AC于点K ，GF交BC于点H，GH：GK的值是否改变？证明你发现的结论；

28. (本题10分)西北某地区为改造沙漠，决定从2002年起进行“治沙种草”，把沙漠地变为草地，并出台了一项激励措施：在“治沙种草”过程中，每一年新增草地面积达到10亩的农户，当年都可得到生活补贴费1500元，且每超出一亩，政府还给予每亩a元的奖励.另外，经治沙种草后的土地从下一年起，平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况：

年　份	新增草地的亩数	年总收入
2002年	20亩	2600元
2003年	26亩	5060元

(注：年总收入＝生活补贴费＋政府奖励费＋种草收入)

⑴试根据以上提供的资料确定a，b的值；

⑵从2003年起，如果该农户每年新增草地的亩数均能比前一年按相同的增长率增长，那么2005年该农户通过“治沙种草”获得的年总收入将达到多少元？

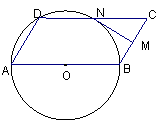
29. （8分）在平行四边形ABCD中，AB=2，∠A=60º，以AB为直径的⊙O过点D，点M是BC边上一点（点M不与B 、C重合），过点M作BC的垂线MN，交CD边于点N．

（1）求AD的长；

（2）如图，当点N在⊙O上时，求证：直线MN是⊙O的切线；

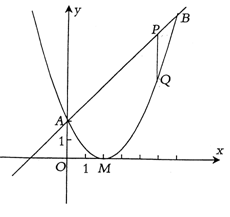
30.（12分）已知二次函数图象的顶点坐标为M(2，0)，直线y＝x+2与该二次函数的图象交于A、B两点，其中点A在y轴上(如图示)

（1）求该二次函数的解析式；

★（2）P为线段用上一动点(A、B两端点除外)，过P作x轴的垂线与二次函数的图象交于点Q，设线段PQ的长为，点P的横坐标为x，求出与x之间的函数关系式，并求出自变量x的取值范围；

（3）在（2）的条件下，线段AB上是否存在一点P，使四边形PQMA为梯形．若存在，求出点P的坐标，并求出梯形的面积；若不存在，请说明理由．

www.1230.org 初中数学资源网 收集整理