九年级第三次月考数学试题
班级 姓名 成绩
（满分：150分；考试时间：100分钟）
考生注意：本卷中凡涉及实数运算，若无特别要求，结果应该为准确数。
一． 填空题：本大题共10小题，1～6题，每小题3分，7～10题，每小题4分，计34分。把答案填在题中横线上。
1．函数y=ax2（a≠0）的图象是________，它的对称轴是________，它的顶点坐标是________．
2.化简：
.
3．“异性电荷相吸引”是__________事件；“掷一枚骰子时一点和三点同时向上”是__________事件；“明天可能下雨”是__________事件。(“必然”、“不可能”或“随机”)
4．已知⊙O中，弦AB的长是8cm，圆心O到AB的距离为3cm，则⊙O的直径是_____cm．
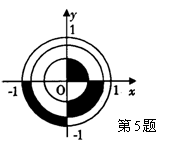
5．如图所示，三个圆是同心圆，图中阴影部分的面积为______．
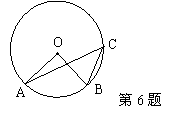
6．如图，点A、B、C三点在⊙O上，且
，则
。
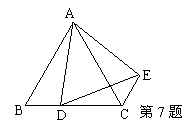
7．如图，等边△ABC的边BC上一点D，△ABD绕点A旋转到△ACE，
则∠DAE＝ °
 | |||||
 | |||||
 | |||||
8．如果圆锥母线长为5cm，高为3cm，那么这个圆锥的侧面积是_______cm2．
9．一个直角三角形的两条直角边长是方程
的两个根，则此直角三角形外接圆的半径等于
。
10．把抛物线y=2x2 先向上平移1个单位，得到抛物线____ ___，再把它向左平移3 个单位，又得到抛物线_____ ___．
二． 选择题：本大题共6小题，每小题4分，计24分。在每小题给出的四个选项中，只有一项是符合题目要求的。
11．如图所示的四个图形中，既可以通过轴对称变换，又可以通过旋转变换得到的图形是（ ）
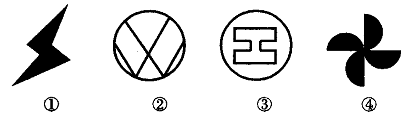
A．①②③④ B．①②③ C．①③ D．③
12.小明的作业本上有以下四题：①
；②
；③
；④
，做错的题是 （ ）
A．① B．② C．③ D．④
13．若
是关于x的二次函数，则a的值是（ ）
A．1 B．-1 C．
D．以上答案都不对
14.抛物线y＝x2＋2x－2的顶点坐标是 （ ）
A.（2，－2） B.（1，－2） C.（1，－3） D.（－1，－3）
15．中央电视台“幸运52”节目中，开设一个幸运观众的“金花四溅”的节目，节目中准备了三个金蛋，三个银蛋，观众任选一个敲碎时，若能从中溅出金花，即可中奖，一次节目游戏中三个金蛋都有金花，一个银蛋中有金花，若某名幸运观众从六个中任选一个，他可以得到“金花四溅”而中奖的概率是（ ）
A．
B．
C．
D．
16． 二次函数y=ax2+bx+c(a≠0)的图像如图所示，下列结论：
(1)c ＜ 0，(2)b ＞ 0， (3)a+b+c＞0 (4) a-b+c＞0
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
三、解答题：本大题共10小题，计92分。解答应写出说理、证明过程或演算步骤
17.（6分）计算
－（2＋
）2
18．（6分）求出抛物线y=x2-5x+6与x轴交点坐标。
19．（8分）已知抛物线的顶点坐标是（-2，1），且过点（1，-2），求此抛物线的解析式。
20．（8分）小明家里的阳台地面，水平铺设着仅黑白颜色不同的18块方砖(如图)，他从房间里向阳台抛小皮球，小皮球最终随机停留在某块方砖上。
（1）求小皮球分别停留在黑色方砖与白色方砖上的概率；(6分)
（2）上述哪个概率较大？要使这两个概率相等，应改变第几行第几列的哪块方砖颜色？怎样改变？(2分)
 |
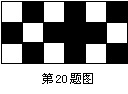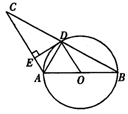
21．（8分）如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC．求证：DE是⊙O的切线。
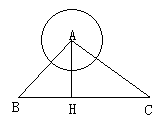
22．（10分）如图，点A是一个半径为300m的圆形森林公园的中心，在森林公园附近有B、C两个村庄，现要在B、C两村庄之间修一条长为1000m的笔直公路将两村连通．经测得∠ABC=45°，∠ACB=30°，问此公路是否会穿过森林公园？请通过计算进行说明．
23．（10分）已知关于x的二次方程x2－（k+2）x+ 2k=0．
（1）求证：无论K取任何实数值时，方程总有两个实数根；（5分）
（2）若等腰三角形的一边长为1，另两边长恰是这个方程的两个根，求三角形的周长。（5分）
24．（12分）某个体户经营一种水产品，成本是每千克40元，经试销发现若按每千克50元销售，一个月能售出500千克；但是售价每涨1元，月销售量就会减少10千克，针对以上情况，请解答下列问题：
（1） 当销售单价为每千克55元时，月销售量和月利润各是多少？
（2） 设销售单价为每千克x元，月销售利润为y元，试写出y与x的函数关系式。（3）你认为销售单价定为多少元时，个体户能获得最大利润？
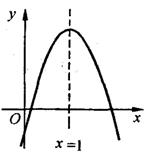
25．（本小题满分12分）已知二次函数
的图象与y轴相交于点(0，－3)，并经过点(－2，5)，它的对称轴是x=1，如图为函数图象的一部分。
（1）求函数解析式，写出函数图象的顶点坐标；(7分)
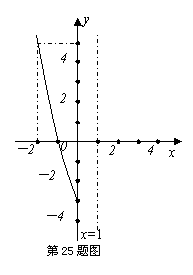（2）在原题图上，画出函数图象的其余部分；(2分)
（3）如果点P(n，－2n)在上述抛物线上，求n的值。(3分)
26．（12分）阅读下面的材料，并解答后面的各题：
在形如ab＝N的式子中，我们已经研究过两种情况：
（1）已知a和b，求N，这是乘方运算；
（2）已知b和N，求a，这是开方运算。
现在，我们研究第三种情况：已知a和N，求b，我们把这种运算称为对数运算。
定义：如果ab＝N（a >0, a≠1, N>0）,则b叫做以a为底N的对数，记作b＝logaN.
例如，因为23＝8，所以log28＝3；因为2－3＝，所以log2＝－3.
（1）（8分）根据定义计算：①log381＝______；②log33＝______；③log41＝______；
④若logx16＝4,则；x＝________；
（2）（4分）设ax＝M, ay＝N,则logaM＝x，logaN＝y( a >0, a≠1,M,N均为正数) .
∵ax·ay＝ax＋y,∴ax＋y＝M·N. ∴loga(MN) ＝x＋y，
即loga(MN) ＝logaM＋logaN.
这是对数运算的重要性质之一。进一步地，我们可以得出：
loga(M1 M2 M3…Mn) ＝_________________________________(其中M1 ,M2, M3,…,Mn均为正数，a >0, a≠1)；loga＝______________（M,N均为正数，a >0, a≠1）。
附加题．（本题满分10分）
友情提示：你已完成上面全部试题，请再认真核查一遍，并自我评价得分情况。如果你估计自己整卷得分低于90分(及格线)，请再完成本大题，将补加1～10分，并计入你的全卷总分；如果你的上面整卷得分已经达到或超出90分，本大题将不再进行批阅。
01．列代数式：a与2的和。(4分)
02．已知等边三角形ABC的一边AB=3，求它的周长。(3分)
03．求：3、2、6、1、3这组数的平均数。(3分)