九年级上期中数学试题
（1～5章）（实验班）
（考生注意： 填空题和选择题答案写在第二张试卷答题卡上，考生只交第二张试卷）
一、选择题（每小题3分，共30分）
1、小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（ ）
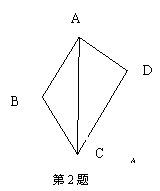A、矩形 B、正方形
C、等腰梯形 D、无法确定
2、如图，四边形ABCD中，∠BAD=90°，AB=BC=，AC=6，AD=3，则CD的长是( )
（A）4 （B）
（C）
（D）
3、“圆柱与球的组合体”如右图所示，则它的三视图是（ ）
A． B． C． D．
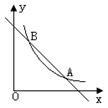
4、如图，在直角坐标系中，直线y=6-x与函数y=
(x＞0)的图象
相交于点A、B，设点A的坐标为(x1，，y1)，那么长为x1,宽为y1
的矩形的面积和周长分别为（ ）
A、4，12 B、8，12 C、4，6 D、8,6
（4题图）
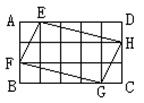
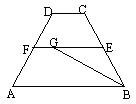
5、如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别
在AD、AB、BC、CD边上，且是某个小正方形的顶点.若四边形EFGH
的面积为1,则矩形ABCD的面积是（ ）
A、2 B、
C、
D、
（5题图）
6、如图，□ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的
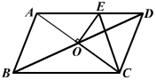周长为（ ）
A、4 cm B、6cm C、8cm D、10cm
（6题图）
7、如图，已知EF是梯形ABCD的中位线，若AB＝8，BC＝6，
CD＝2，∠B的
平分线交EF于G，则FG的长是（ ）
A、1 B、1.5 C、2 D、2.5
（7题图）
8、如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）。按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（ ）
A、都是等腰梯形 B、都是等边三角形
C、两个直角三角形，一个等腰三角形 D、两个直角三角形，一个等腰梯形
9、小明、小亮、小梅、小花四人共同探讨代数式x2－4x+5的值的情况．他们作了如下分工：小明负责找其值为1时的x的值，小亮负责找其值为0时的x的值，小梅负责找最小值，小花负责找最大值。几分钟后，各自通报探究的结论，其中错误的是（ ）
A、小明认为只有当x=2时，x2－4x+5的值为1
B、小亮认为找不到实数x，使x2－4x+5的值为0
C、小梅发现x2－4x+5的值随x的变化而变化，因此认为没有最小值
D、小花发现当x取大于2的实数时，x2－4x+5的值随x的增大而增大，因此认为没有最大值
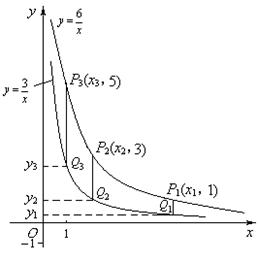10、两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2 005，纵坐标分别是1，3，5，…，共2
005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
（10题图）
二、填空题（每小题3分，共24分）
11、方程x(x+3)=x+3的解是 。
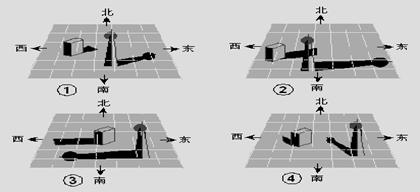12、下面是一天中四个不同时刻两个建筑物的影子：
将它们按时间先后顺序进行排列为 。
13、设有反比例函数
，
、
为其图象上的两点，若
时，
，则
的取值范围是
。
14、一跳水运动员从10米高台上跳水，设他在起跳后第t秒离水面的高度为h米，且h=-5t2+5t+10，
则运动员从起跳到入水所用的时间为 。
15、如图，以正方形ABCD的对角线AC为一边，延长AB到E，
使AE=AC，以AE为一边作菱形AEFC若菱形的面积为
，
则正方形的边长为__________。
|
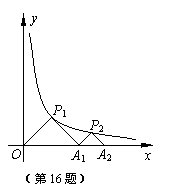16、如图，△P1O A1、△P2 A1 A2是等腰直角三角形，点P1、P2在函数
（x＞０）的图象上，斜边OA1、A1A2都在x轴上，则点A 2
的坐标是 。
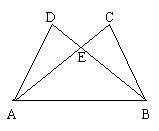17、如图，给出五个等量关系：①AD=BC、②AC=BD、③CE=DE、
④∠DAB=∠CBA、⑤∠D=∠C。请你以其中两个为条件，另三个中的一个为结论，写出一个正确的命题 。
（第17题）
18、如图，将边长为2cm的两个互相重合的正方形纸片按住其中一个不动，另一个纸点B顺时针旋转一个角度，若使重叠部分的面积为cm2，则这个旋转角度为________度。
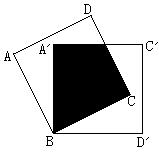
（第18题）
答题卡
一、选择题：（每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题：每小题3分，共27分）
1、 2、 3、 4、
5、 6、 7、 8、
9、 10、 11、 12、
13、 14、 15、 16、
17、 18、
三、解答题:（共66分）
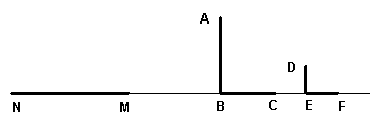
19、如图，路灯下，一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN，在图中画出表示大树高的线段MP。（4分）
20、已知实数a满足a2＋2a－8=0，求
的值.（7分）
21、阅读下面的例题： （6分）
解方程：
.
解：原方程可化为：
即：
.
∵
＞0
∴
∴
∴原方程的根是
请参照例题解方程：
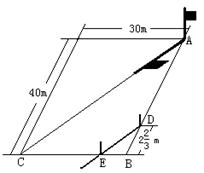22、如图，在一个长40m、宽30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地。当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距B地2m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上。此时，A处一根电线杆在阳光下的影子也恰好落在对角线AC上。
⑴求他们的影子重叠时，两人相距多少米(DE的长)？
⑵求张华追赶王刚的速度是多少(精确到0.1m/s)？（10分）
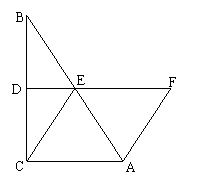23、如图，在Rt△ABC中，∠ACB = 90°，∠BAC
= 60°，DE垂直平分BC，垂足为D，交AB于点E。又点F在DE的延长线上，且AF = CE。试猜测四边形ACEF的形状,并证明你的猜想。（9分）
24、《中华人民共和国道路交通安全法实施条例》中规定：超速行驶属违法行为。为确保行车安全，一段高速公路全程限速110千米/时（即任一时刻的车速都不能超过110千米/时）。以下是张师傅和李师傅行驶完这段全程为400千米的高速公路时的对话片断。张：“你的车速太快了，平均每小时比我多跑20千米，少用我1小时就跑完了全程，还是慢点。”李：“虽然我的时速快，但最大时速也不超过我平均时速的10％，可没有超速违法啊。”李师傅超速违法吗？为什么？（8分）
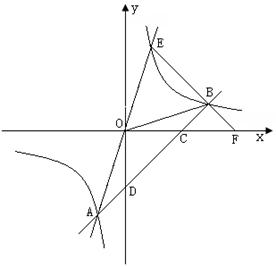
25、如图，直线
与双曲线
相交于点A、E。另一直线
与双曲线交于点A、B，与x、y轴分别交于点C、D。直线EB交x轴于点F。
（1）求A、B两点的坐标，并比较线段OA、OB的长短；
（2）由函数图象直接写出函数
＞
＞
的自变量x的
取值范围；
（3）求证：△COD∽△CBF。（10分）
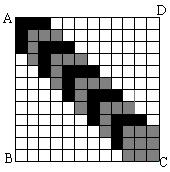
26、如图，正方形ABCD的边长为12，划分成12×12个小正方形格。将边长为n×n(n为整数，且
2≤n≤11)的两种颜色正方形纸片按图中的方式相间摆放。第一张n×n的纸片正好盖住正方形ABCD
左上角的n×n个小方格，第二张纸片盖住第一张纸片的部分恰好为（n-1）×(n-1)的正方形。如此
摆放下去，最后直到纸片盖住正方形ABCD的右下角为止。
请你认真观察思考后回答下列问题：
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 |
（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同。请填写下表：
（2）正方形ABCD被纸片盖住的面积（重合部分只计一次）为S1，未被盖住的面积为S2
①当n=2时，求S1 ：S2的值。
②是否存在使得S1 =S2的n值，若存在，求出这样的n值；若不存在，请说明理由。
（右边两张方格纸供作草稿用）（12分）
 | |